oa9

3. 3corr

Segundo Teorema de Tales

Si un haz de rectas es cortado por dos o más paralelas, los trazos paralelos interceptados están en la misma razón que los respectivos segmentos determinados sobre una misma recta del haz.

Hipótesis: \(\; AB \parallel CD\)

Tesis:

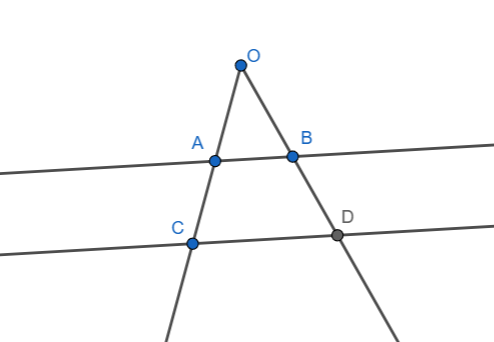
Figura Segundo Teorema de Tales

\(\displaystyle \frac{AB}{CD} = \frac{OB}{OD}\)
\(\displaystyle \frac{AB}{CD} = \frac{OA}{OC}\)

Demostración

Demostraremos la primera proporción (\(\;\frac{AB}{CD} = \frac{OB}{OD}\); la segunda es análoga):

Prueba:

I. Se trazará por B un segmento paralelo a \(OC\), determinando el punto E.
II. El triángulo \(\triangle ODC\) es cortado por las paralelas \(BE\) y \(OC\), así que podemos usar el Primer Teorema de Tales para establecer:

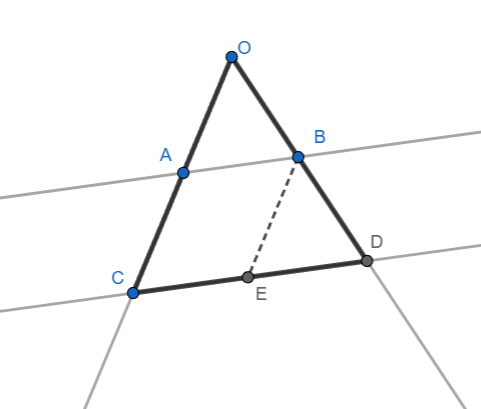
Figura de la demostración T.2

\(\displaystyle \frac{OB}{OD} = \frac{CE}{CD}.\)

III. Observa que con el segmento BE se forma el paralelogramo CEBA, por lo que \(\; CE = AB\).

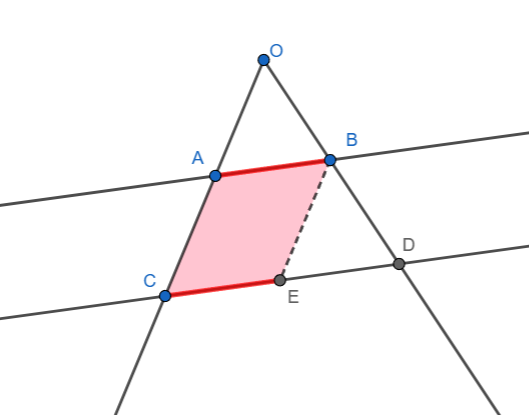
Paralelogramo CEBA

Entonces, reemplazando \(CE\) por \(AB\) en la proporción anterior:

\(\displaystyle \frac{OB}{OD} = \frac{AB}{CD}\quad (\text{Q.E.D.})\)

Paralelas opuestas por el vértice

Si las paralelas están opuestas por el vértice, puede demostrarse de forma análoga (giro de 180°) que se cumplen las mismas relaciones.

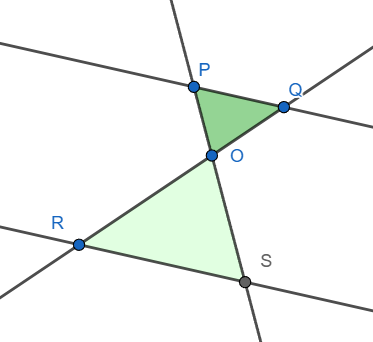
Figura opuestas vértice - Segundo Teorema de Tales

\(\displaystyle \frac{QP}{RS} = \frac{OP}{OS}\), \quad \(\displaystyle \frac{QP}{RS} = \frac{OQ}{OR}\).

Puedes girar la figura 180° moviendo el desplazador para observar cómo se deduce la propiedad en este caso.