Relación entre Homotecias y el Teorema de Tales

Las homotecias y el Teorema de Tales están intrínsecamente relacionados. El Teorema de Tales, en su forma más general, puede considerarse una consecuencia directa de las propiedades de las homotecias. Para entender esta relación, primero definamos ambos conceptos.

Definiciones

Homotecia

recoredemos que una homotecia es una transformación geométrica que, a partir de un punto fijo \(O\) (llamado centro de homotecia) y una razón \(k\) (un número real distinto de cero), transforma un punto \(P\) en un punto \(P'\) de tal manera que:

• \(O\), \(P\) y \(P'\) son colineales (están en la misma línea recta).
• La razón de las distancias \(OP'\) a \(OP\) es igual a \(k\), es decir: \(\frac{OP'}{OP} = k\).

Si \(k > 0\), la homotecia se llama directa.
Si \( k < 0 \), se denomina inversa (el punto imagen esta "detras" del centro de homotecia).
Si \(|k| > 1\), la figura resultante es una ampliación.
Si \(0 < |k| < 1\), la figura resultante es una reducción.

Teorema de Tales

Forma básica (triángulos): Si dos rectas cualesquiera son cortadas por rectas paralelas, los segmentos que determinan en una de las rectas son proporcionales a los segmentos correspondientes de la otra.

En un triángulo \(ABC\), si trazamos una línea \(B'C'\) paralela al lados \(BC\), entonces se cumple:

Forma general (con varias paralelas): Dadas varias rectas paralelas cortadas por dos rectas secantes, los segmentos determinados en una secante son proporcionales a los segmentos correspondientes en la otra secante.

La Relación

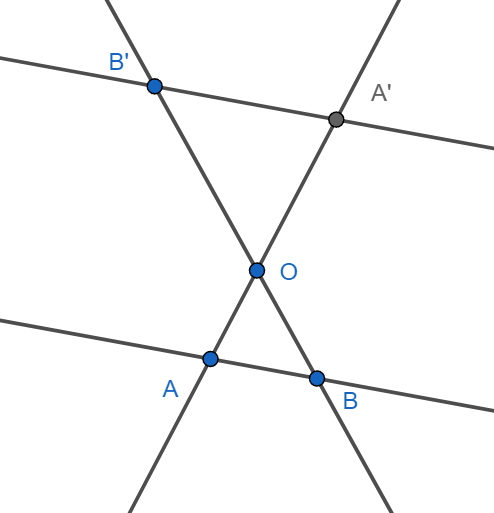
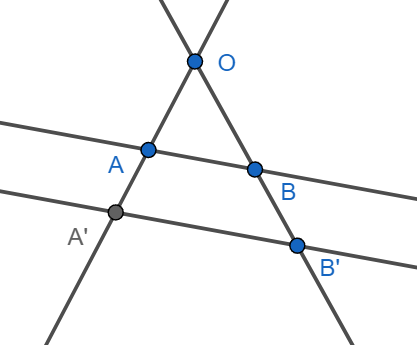
La relación clave es la siguiente: El Teorema de Tales describe, esencialmente, el efecto de una homotecia *sin mencionar explícitamente la homotecia*. Consideremos la forma básica del Teorema de Tales en un triángulo \(OAB\) con \(A'B'\) paralela a \(AB\).

Podemos ver el triángulo \(OA'B'\) como el resultado de aplicar una homotecia al triángulo \(OAB\) con centro en el vértice \(O\) y una razón \(k = \frac{OA}{OA'}\). Como \(AB\) es paralela a \(OA\), las líneas que conectan los vértices correspondientes (\(A\) con \(A'\), y \(B\) con \(B'\)) concurren en el centro de homotecia \(A\). La proporcionalidad dada por el Teorema de Tales:

...es *exactamente* la definición de la razón de homotecia. La homotecia "estira" o "encoge" el triángulo \(OAB\) a lo largo de las líneas que pasan por \(O\), manteniendo las proporciones. La forma general del Teorema de Tales es simplemente la aplicación de esta idea a múltiples segmentos y rectas paralelas, todos "estirados" o "encogidos" por la misma homotecia.

Ejemplos

1. Arquitectura y Escalas

Los planos arquitectónicos son un ejemplo perfecto de homotecias. Cuando se crea una maqueta a escala de un edificio, se está aplicando una homotecia. El centro de homotecia podría ser, conceptualmente, un punto en el espacio desde el cual "proyectamos" el edificio real para obtener la maqueta. La razón de homotecia sería la escala del plano (por ejemplo, 1:100). Las proporciones entre las diferentes partes del edificio (ventanas, puertas, altura de los pisos) se mantienen gracias al Teorema de Tales, que, como vimos, es una consecuencia directa de la homotecia. Si dos paredes son paralelas en la realidad, también lo serán en la maqueta.

2. Fotografía y Proyección

Cuando tomas una fotografía, la lente de la cámara realiza (aproximadamente) una homotecia. El centro de homotecia es el centro óptico de la lente. Los rayos de luz que provienen de un objeto (el "original") pasan por el centro de la lente y forman una imagen invertida (homotecia inversa, \(k < 0\)) en el sensor (o película). La razón de homotecia depende de la distancia focal de la lente y la distancia al objeto. El Teorema de Tales se manifiesta en que líneas paralelas en el mundo real (como los bordes de un edificio) generalmente aparecen como líneas convergentes en la fotografía (a menos que sean paralelas al plano del sensor), pero las *proporciones* entre las partes del edificio se conservan en la imagen formada en el sensor, gracias a la homotecia y, por tanto, al Teorema de Tales.

3. Sombras Proyectadas

Una sombra proyectada por un objeto y una fuente de luz puntual es una homotecia. La fuente de luz actúa como el centro de homotecia. La razón de homotecia está determinada por la relación entre la distancia de la fuente de luz al objeto y la distancia de la fuente de luz a la superficie donde se proyecta la sombra. El Teorema de Tales se puede usar para calcular la longitud de la sombra, conociendo la altura del objeto y las distancias. Si tienes dos objetos de diferente altura, sus sombras (si son proyectadas por la misma fuente de luz y sobre la misma superficie) tendrán longitudes proporcionales a sus alturas. Esto es el Teorema de Tales en acción.

4. Microscopía

En microscopía, se utilizan lentes para ampliar la imagen de un objeto pequeño. El sistema de lentes crea una serie de homotecias. La lente objetiva forma una imagen real, invertida y aumentada del objeto (una homotecia inversa con |k| > 1). Luego, la lente ocular toma esta imagen real y la amplía aún más, formando una imagen virtual que es la que ve el observador. Aunque hay múltiples etapas de ampliación, el principio fundamental es el mismo: la imagen final es una homotecia (o una composición de homotecias) del objeto original. Las proporciones dentro del objeto se conservan gracias al Teorema de Tales.

5. Semejanza de Triángulos

Dos triángulos son semejantes si tienen los mismos ángulos y sus lados correspondientes son proporcionales. La semejanza de triángulos es un caso especial del Teorema de Tales y, por tanto, una manifestación de las homotecias. Si tienes dos triángulos semejantes, siempre puedes encontrar una homotecia (y quizás una rotación y/o traslación) que transforme uno en el otro. La razón de semejanza entre los triángulos es la misma que la razón de la homotecia.

Conclusión

En resumen, el Teorema de Tales y las homotecias están profundamente interconectados. El Teorema de Tales puede verse como una descripción de las consecuencias de una homotecia en términos de proporcionalidad de segmentos. Las homotecias proporcionan el marco geométrico subyacente que explica por qué el Teorema de Tales funciona. Esta relación se manifiesta en numerosos ejemplos del mundo real y en aplicaciones matemáticas.