semejanzas y escalas
1. Diferencia geométrica entre congruencia, equivalencia y semejanza
Preguntas y Respuestas - Semejanza y CongruenciaDiferencia geométrica entre congruencia, equivalencia y semejanza
En geometría, es fundamental comprender las relaciones entre las figuras. Aquí te presento las diferencias entre tres conceptos clave:
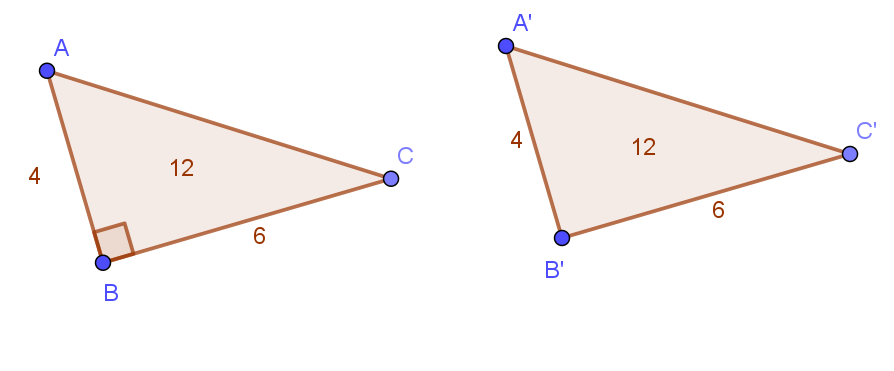
Congruencia
Dos figuras son congruentes si tienen la misma forma y tamaño. Imagina dos monedas idénticas: son congruentes.
Equivalencia
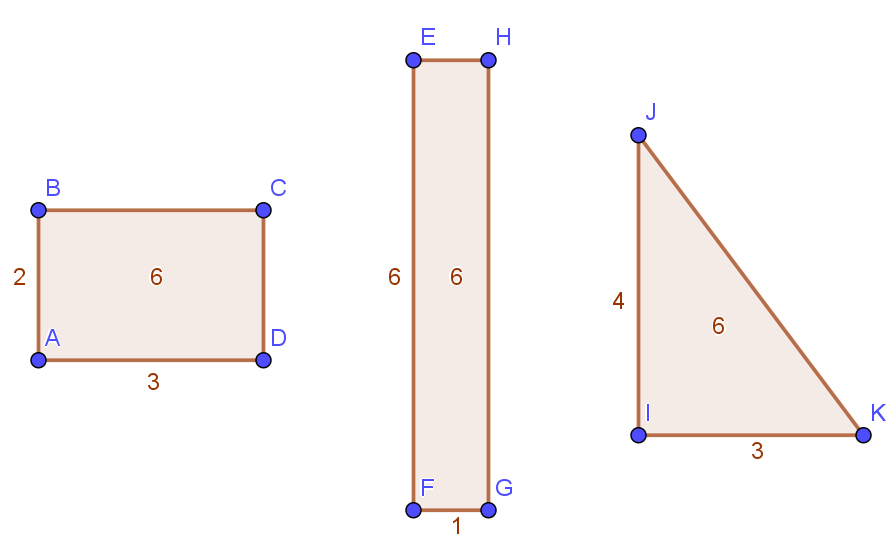
Dos figuras son equivalentes si tienen la misma área, pero no necesariamente la misma forma. Un triángulo y un rectángulo pueden ser equivalentes si ambos encierran la misma superficie.
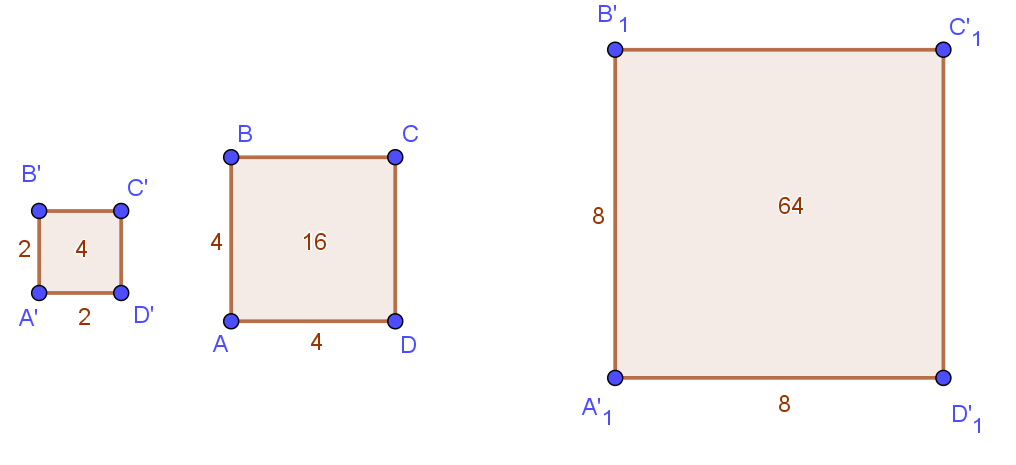
Semejanza
Dos figuras son semejantes si tienen la misma forma, pero pueden tener diferente tamaño. Una fotografía y su versión en miniatura son semejantes.
En resumen:
- Congruencia: Igual forma y tamaño.
- Equivalencia: Igual área (misma superficie), forma puede variar.
- Semejanza: Igual forma, tamaño puede variar (escalado).
Explorando la congruencia, semejanza y equivalencia de figuras
En la siguiente actividad, interactuarás con un applet de GeoGebra donde podrás visualizar cómo se relacionan las figuras bajo diferentes transformaciones geométricas. Al mover los puntos en las figuras, observarás cómo cambian las longitudes y posiciones de los lados, y cómo las líneas que unen los vértices correspondientes se comportan en los casos de congruencia, semejanza y equivalencia.
1. ¿Cómo son las líneas que unen los vértices correspondientes en figuras congruentes?
2. ¿En qué se parecen y en qué se diferencian las figuras congruentes y las figuras semejantes?
3. En el caso de figuras equivalentes, ¿qué sucede si modifico la medida de uno de sus lados?
4. ¿Es posible que dos figuras sean semejantes pero no equivalentes? ¿Y al revés? Explica con ejemplos.
5. Si una figura es semejante a otra, ¿cómo se relacionan sus perímetros y áreas?
6. Si dos figuras son semejantes, ¿podrían ser también congruentes? Explica en qué condiciones sucede esto.
7. En figuras equivalentes, ¿qué propiedades geométricas se conservan y cuáles cambian?
8. ¿Es correcto afirmar que una figura congruente es una combinación de semejanza y equivalencia? Justifica tu respuesta.