Organización de Datos en Tablas e Interpretación Gráfica

Importancia de la Organización de Datos

Antes de calcular medidas de dispersión (rango, varianza, desviación estándar), es crucial organizar los datos de manera clara y sistemática. Las tablas son una herramienta esencial para esto. Además, la representación gráfica (histogramas y diagramas de caja) nos da una idea visual rápida de la distribución y dispersión de los datos.

Tipos de Tablas

1. Tabla de Datos Simple (o Lista de Datos)

La forma más básica es listar los datos. Adecuado para conjuntos pequeños.

Ejemplo: Alturas (cm) de 5 estudiantes: 160, 165, 170, 172, 168

2. Tabla de Frecuencias

Para datos repetidos, una tabla de frecuencias es más eficiente. Muestra cada valor único y su *frecuencia* (cuántas veces aparece).

Ejemplo: Edades: 20, 22, 20, 21, 22, 20, 23, 22, 20, 21

Frecuencia Relativa: Frecuencia de un valor dividida por el total. Se expresa como fracción, decimal o porcentaje.

3. Tabla de Frecuencias con Datos Agrupados (Intervalos)

Para muchos datos diferentes, o datos continuos, se agrupan en *intervalos* o *clases*.

Ejemplo: Alturas (en cm) de 40 estudiantes (lista omitida por brevedad).

Consideraciones al agrupar en intervalos:

• Intervalos del mismo tamaño (amplitud).
• Intervalos no superpuestos.
• Cubrir todos los datos (mínimo a máximo).
• Entre 5 y 15 intervalos (regla práctica: raíz cuadrada del número de datos).

Preparación de Datos para el Cálculo de Medidas de Dispersión

Con los datos en tablas (especialmente de frecuencias), es más fácil calcular las medidas:

• Rango: Valor máximo - valor mínimo (o límites de los intervalos).
• Varianza y Desviación Estándar:
  • Datos sin agrupar: Usar la tabla para calcular la media y las desviaciones.
  • Datos agrupados: Usar el *punto medio* (marca de clase) de cada intervalo.

Interpretación Visual de la Dispersión: Histogramas y Diagramas de Caja

Histogramas

Un histograma (gráfico de barras "pegadas" para representar continuidad) muestra la distribución de frecuencias de la variable. Permite *estimar* visualmente la media y la desviación estándar.

Estimación de la Media:

• "Punto de equilibrio" del histograma.
• Simétrico: media en el centro.
• Asimétrico (sesgado): media desplazada hacia la "cola".

Estimación de la Desviación Estándar:

• Relacionada con el "ancho" del histograma.
  • Ancho y plano: *alta* desviación estándar (datos dispersos).
  • Estrecho y alto: *baja* desviación estándar (datos concentrados).
• Regla Empírica (aproximada, solo para distribuciones aproximadamente normales):
  • Aprox. 68% de los datos: ±1 desviación estándar de la media.
  • Aprox. 95% de los datos: ±2 desviaciones estándar de la media.
  • Aprox. 99.7% de los datos: ±3 desviaciones estándar de la media.

  Ejemplo: Si el 95% de los datos está entre 50 y 70, la desviación estándar es aproximadamente (70-50)/(2*2) = 5.

  Advertencia: La regla empírica es solo una *aproximación* para distribuciones *aproximadamente normales*.

Ejemplos: 

Ejemplo 1: Histograma alto y estrecho, centrado en 80. Media ≈ 80, Desviación estándar pequeña.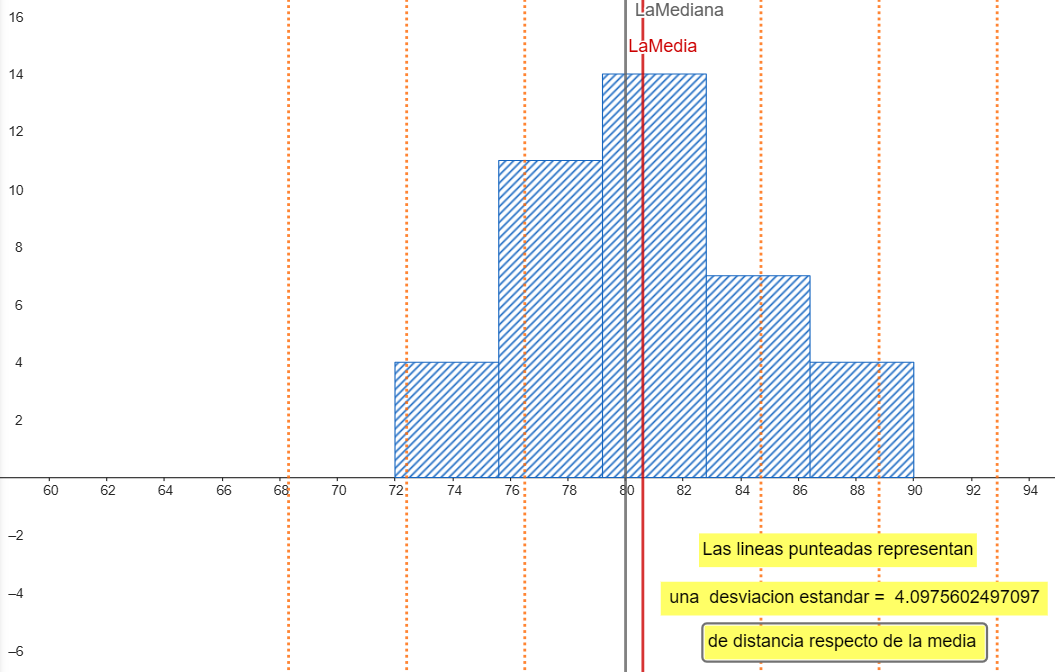

Ejemplo 2: Histograma sesgado a la izquierda. Media > Mediana. Desviación estándar mayor que si fuera simétrico.

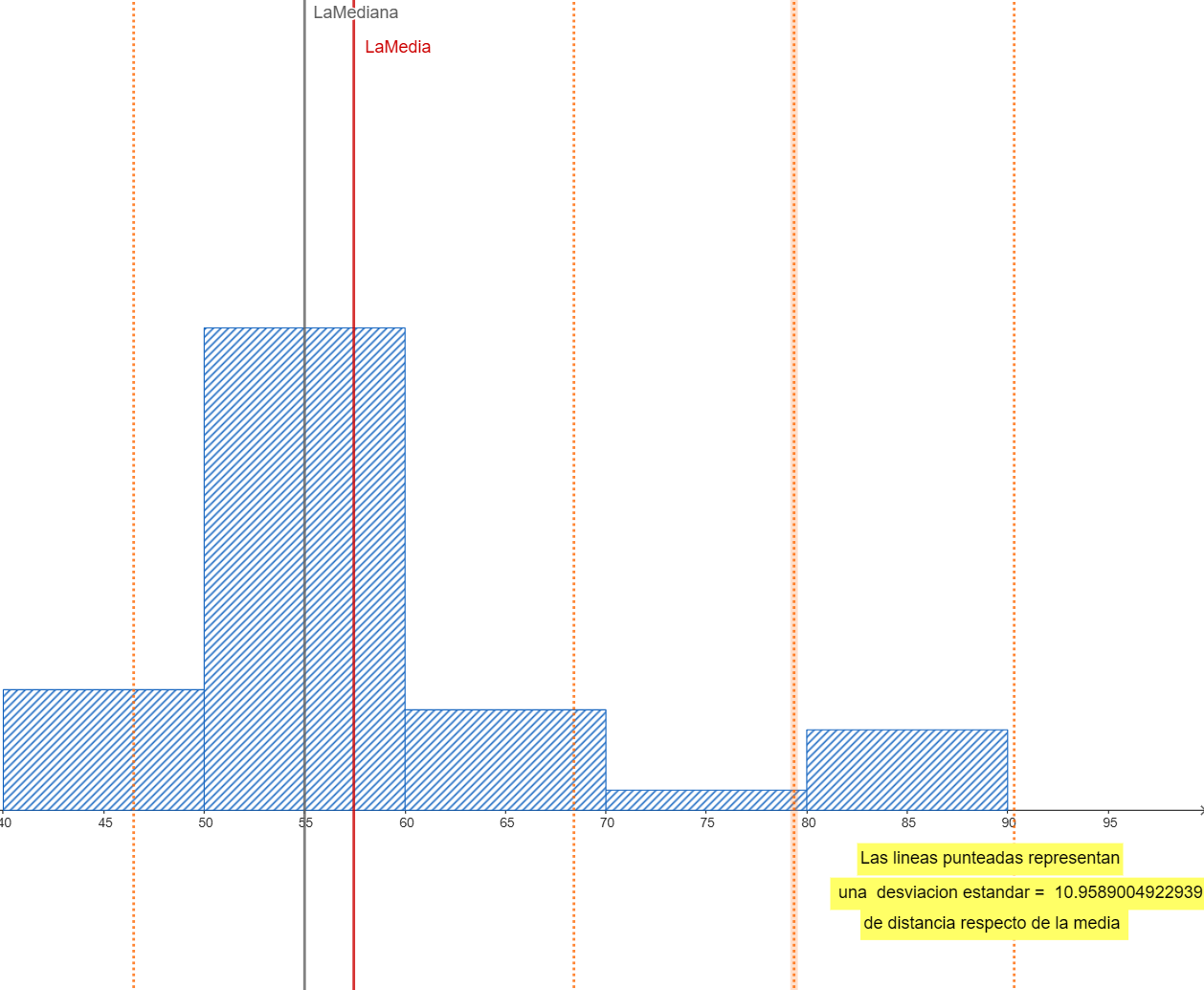
Ejemplo 3: Histograma ancho y plano, de 20 a 80. Media ≈ 50, Desviación estándar grande.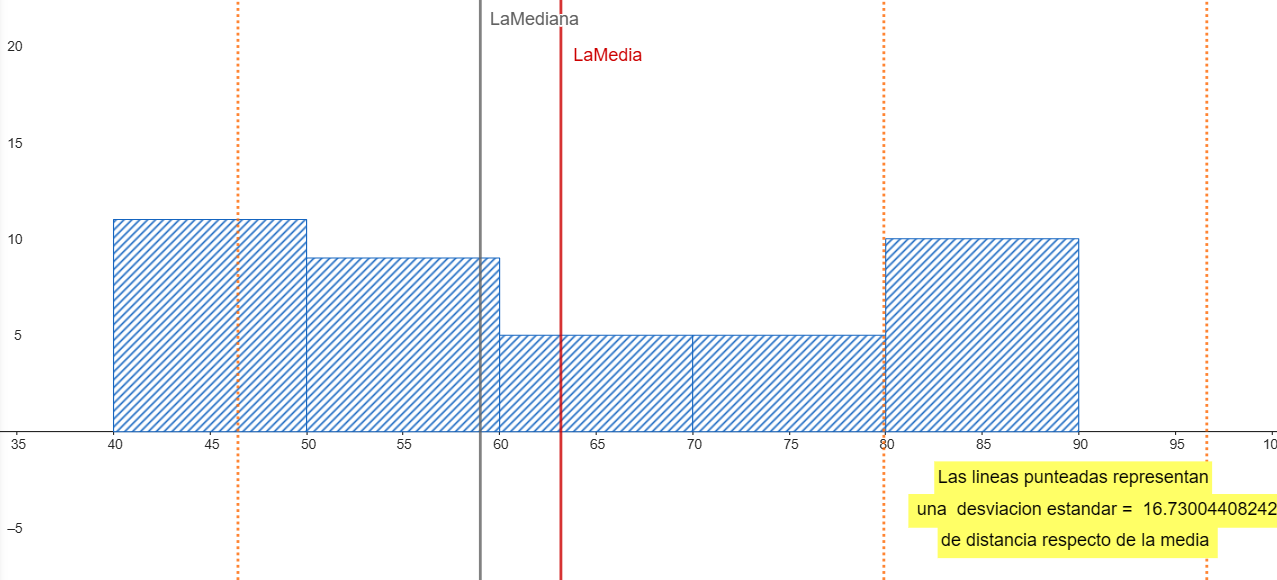

Diagramas de Caja (Boxplots)

Muestran un resumen de cinco números: mínimo, Q1 (primer cuartil), mediana, Q3 (tercer cuartil), máximo, y valores atípicos.

• Mediana: Línea dentro de la caja.
• Cuartiles (Q1 y Q3): Bordes de la caja. El 50% de los datos está *dentro* de la caja.
• Rango Intercuartílico (IQR): Q3 - Q1. Medida de dispersión *resistente, es decir no se ve muy afectado por valores extremos como la desviacion estandar*.
• Bigotes: Líneas desde la caja. Generalmente, hasta el máximo y mínimo de valores, siempre y cuando estos esten   a distancia maxima de 1.5 * IQR desde los cuartiles Q1 o Q3 respectivos.
• Valores Atípicos: Puntos individuales fuera de los bigotes, por sobre 1.5 * IQR.
  
  

Estimación de la Desviación Estándar (aproximada, solo para distribuciones aproximadamente normales):

\[ \text{Desviación estándar} \approx \frac{IQR}{1.35} \]

Advertencia: Aproximación para distribuciones *aproximadamente normales*.

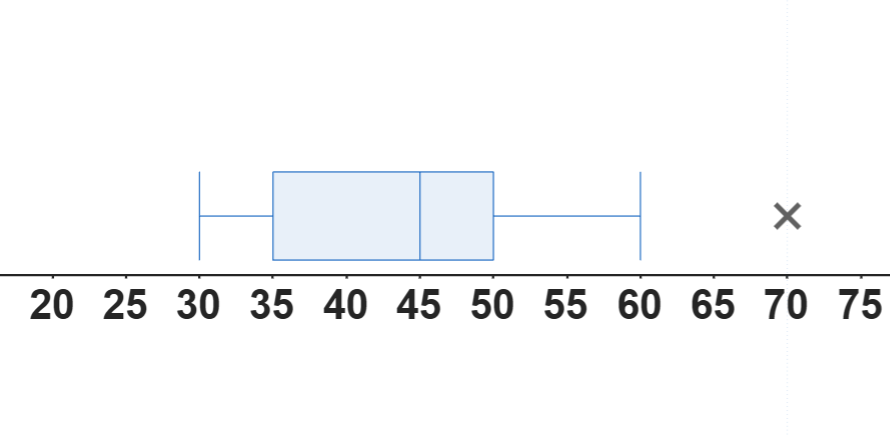
Ejemplo: Mediana = 60, Q1 = 50, Q3 = 70, Bigotes hasta 40 y 80, valor atípico en 95.

• Mediana ≈ 60.
• IQR = 70 - 50 = 20.
• Si suponemos normalidad, Desviación estándar ≈ 20 / 1.35 ≈ 14.8.
• Valor atípico: 95.

Comparación de Boxplots: Comparar el *ancho de las cajas* (IQR) y la *longitud de los bigotes*. Cajas más anchas y bigotes más largos indican mayor dispersión.

Ejemplo: 

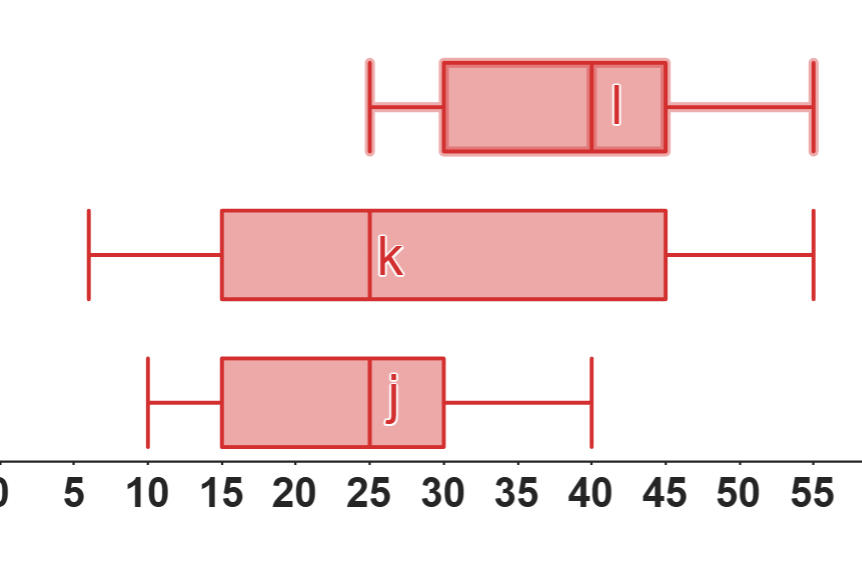
📊 Similitudes:

1. Mediana Común:

   • Los conjuntos j y k tienen la misma mediana (25), lo que indica una tendencia central similar en estos dos conjuntos de datos.

2. Rango Similar:

   • Los conjuntos j y l tienen un rango de 30 unidades (40 - 10 y 55 - 25 respectivamente), lo que indica una dispersión similar en el rango completo de los datos.

3. Rango Intercuartílico (IQR) Igual:

   • Tanto j como l tienen un IQR de 15 (30 - 15 y 45 - 30), mostrando una variabilidad similar en el 50% central de sus datos.

4. Bigotes de Longitud Similar:

   • Los bigotes del conjunto j y l son simétricos y tienen aproximadamente la misma extensión, indicando una distribución equilibrada de los datos fuera del IQR.

📈 Diferencias:

🔍 Resumen de Diferencias:

1. Dispersión:

   • k tiene la mayor dispersión general (mayor rango e IQR).
   • j y l tienen una dispersión similar en el rango total, pero con diferencias en la tendencia central.

2. Ubicación de la Mediana:

   • j y k comparten la misma mediana (25), mientras que l tiene una mediana significativamente más alta (40).

3. Distribución de los Datos:

   • j: Datos concentrados en la parte inferior del rango.
   • k: Gran dispersión con sesgo hacia la derecha.
   • l: Datos concentrados en la parte superior del rango con un sesgo a la izquierda.

🎯 Conclusión:

• Si buscas consistencia, el conjunto j es el más estable.
• Para mayor rango de datos y variabilidad, el conjunto k es el indicado.
• Si prefieres valores más altos en general, el conjunto l es el mejor representante.

Ejercicios y Problemas

  Consultorio B

1.        

1.  
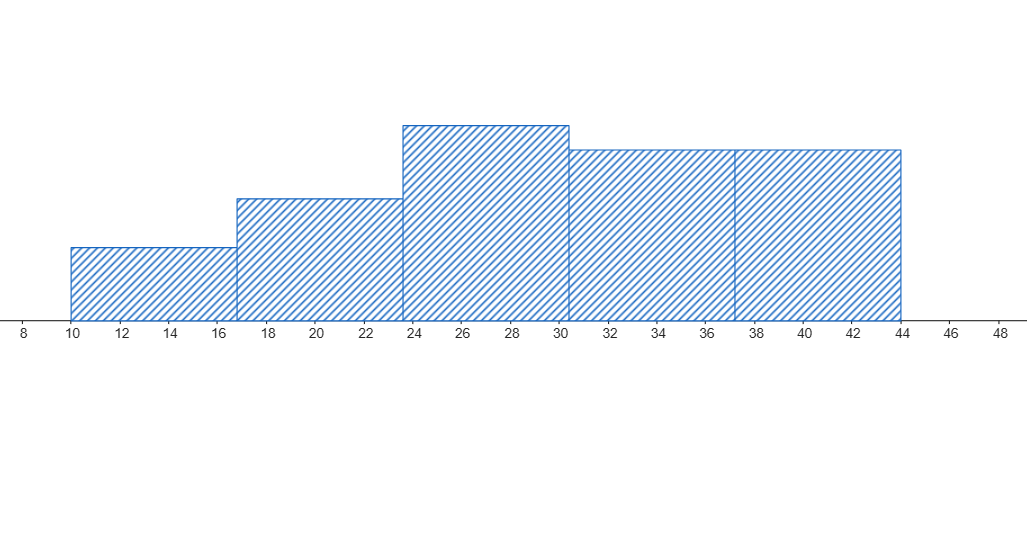
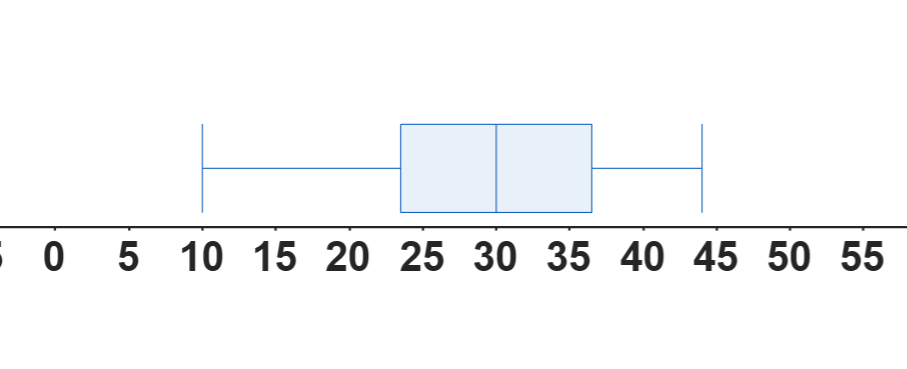
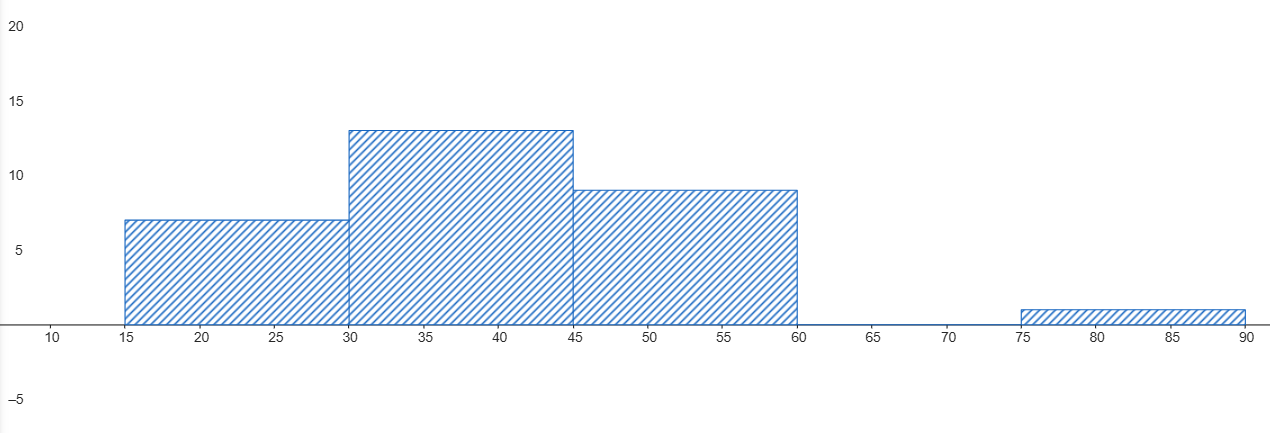
2. ¿Qué consultorio tiene, en promedio, tiempos de espera más largos?
3. ¿En qué consultorio los tiempos de espera son más variables?
4. Si tuvieras prisa, ¿a qué consultorio irías? ¿Por qué?
5. ¿Hay indicios de valores atípicos? De ser así, describe en que consiste.
6. Un analista afirma que: "Como el consultorio A tiene una menor desviación estándar, entonces es *imposible* que un paciente tenga que esperar más tiempo en el consultorio A que en el consultorio B". ¿Es verdadera o falsa esta afirmación? Justifica tu respuesta.

Mostrar/Ocultar Solución

1. Consultorio B (el histograma está más a la derecha, o la mediana del boxplot es mayor).
2. Consultorio B (el histograma es más ancho, o la caja y los bigotes del boxplot son más largos).
3. Consultorio A (menor media y menor dispersión, es más probable un tiempo de espera corto).
4. Sí, en el Consultorio B hay un valor atípico (un punto fuera de los bigotes en el boxplot, o una barra muy alejada en el histograma). Por ejemplo, un paciente que tuvo que esperar mucho más tiempo que la gran mayoría.
5. Falsa. Una menor desviación estándar indica *menor variabilidad* alrededor de la media, pero *no* elimina la posibilidad de que existan valores individuales mayores en el consultorio A que en el B. La desviación estándar es una medida de *dispersión*, no un límite superior. Un solo valor atípico alto en el consultorio A podría ser mayor que *cualquier* valor en el consultorio B, incluso si la desviación estándar de A es menor.

© 2024 - Material de Apoyo