Los números naturales
| Sitio: | PROFEARAUCO.CL |
| Curso: | Media 1 |
| Libro: | Los números naturales |
| Imprimido por: | Invitado |
| Día: | jueves, 22 de enero de 2026, 21:20 |
Descripción
Tabla de contenidos
- 1. Los Números Naturales
- 2. Construcción de los Números Naturales a partir de Conjuntos (Complemento optativo)
- 3. Propiedades de los números naturales
- 4. Adición y Sustracción de Números Naturales
- 5. Multiplicación de Números Naturales
- 6. División de Números Naturales
- 7. Criterios de Divisibilidad: ¡Atajos Matemáticos!
- 8. ¡Explorando el Mundo de los Números Primos!
- 9. Máximo Común Divisor (MCD): ¡Encontrando Conexiones!
- 10. Mínimo Común Múltiplo (MCM): ¡Encontrando el Punto de Encuentro!
- 11. Subconjuntos de los Números Naturales: algunas Sucesiones
- 12. Potencias de Números Naturales
- 13. Propiedades de las Potencias
1. Los Números Naturales
Los Números Naturales
Los números naturales son los primeros que aprendemos desde pequeños. Se usan para contar, ordenar cosas y resolver problemas simples. Por ejemplo, cuando cuentas cuántos amigos están contigo o cuántas manzanas tienes, estás usando números naturales. Este conjunto es la base para entender matemáticas más avanzadas.
📐 Definición
Los números naturales son un conjunto que comienza desde el cero y se extiende infinitamente. Se denotan con el símbolo \( \mathbb{N} \).
\( \mathbb{N} = \{0, 1, 2, 3, 4, 5, \dots\} \)
Son infinitos, porque siempre podemos sumar \(1\) a cualquier número y obtener otro número natural.
Usos y Propiedades
🤔 ¿Para qué sirven los números naturales?
Los números naturales se usan para:
- Contar: ¿Cuántos estudiantes hay en una sala? Usamos \(1, 2, 3, \dots\).
- Ordenar: Decir que \(1^\circ\) es el primero, \(2^\circ\) es el segundo, y así sucesivamente.
- Resolver problemas: Si tienes 3 lápices y te regalan 2 más, ¿cuántos tienes en total?
🧐 Propiedades Clave
- Son infinitos: Siempre puedes obtener un número natural mayor sumando 1.
- No tienen números negativos: Comienzan en 0 y solo incluyen números positivos.
- Tienen operaciones básicas: Se pueden sumar, restar (si el resultado no es negativo) y multiplicar.
Ejemplos y Curiosidades
Ejemplos de Operaciones
- Suma: Si tienes 3 libros y compras 2 más, ahora tienes: \( 3 + 2 = 5 \)
- Multiplicación: Si tienes 2 cajas con 5 lápices cada una, en total tienes: \( 2 \cdot 5 = 10 \)
- Orden: Entre los números 2 y 5, sabemos que \(2 < 5\).
⚠️ ¿El Cero es Natural?
¿Sabías que algunos matemáticos no consideran al cero (0) como parte de los números naturales? En algunos libros, el conjunto empieza en 1. Sin embargo, en las matemáticas más modernas y por convención, se incluye al cero.
Conclusión
Los números naturales son la base de las matemáticas y nos ayudan a entender y resolver problemas de la vida diaria. Desde contar hasta realizar operaciones complejas, estos números nos acompañan siempre. ¡Ahora que los conoces mejor, úsalos con confianza!
2. Construcción de los Números Naturales a partir de Conjuntos (Complemento optativo)
Construcción Formal de los Números Naturales
Los números naturales (\( \mathbb{N} \)) son el conjunto básico sobre el cual se construyen otros sistemas numéricos. En teoría de conjuntos, los números naturales se construyen de manera formal a partir del conjunto vacío (\( \emptyset \)), utilizando únicamente axiomas y reglas lógicas.
📐 Definición Matemática (Construcción de Von Neumann)
Los números naturales pueden definirse utilizando los axiomas de Zermelo-Fraenkel y la siguiente construcción inductiva:
- El Cero: Se define el número \(0\) como el conjunto vacío.
\( 0 = \emptyset \)
- El Sucesor: El sucesor de un número natural \(n\), denotado como \(S(n)\), se define como la unión de \(n\) y el conjunto que contiene a \(n\).
\( S(n) = n \cup \{n\} \)
Construcción de los Primeros Números
Aplicando la definición del sucesor, podemos construir los primeros números naturales:
- \(0 = \emptyset\)
- \(1 = S(0) = 0 \cup \{0\} = \emptyset \cup \{\emptyset\} = \{\emptyset\}\)
- \(2 = S(1) = 1 \cup \{1\} = \{\emptyset\} \cup \{\{\emptyset\}\} = \{\emptyset, \{\emptyset\}\}\)
- \(3 = S(2) = 2 \cup \{2\} = \{\emptyset, \{\emptyset\}\} \cup \{\{\emptyset, \{\emptyset\}\}\} = \{\emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\}\}\)
- Y así sucesivamente... Cada número natural es el conjunto de todos los números naturales que le preceden.
Propiedades y Axiomas
🔍 Propiedades Derivadas
A partir de esta construcción, se derivan propiedades fundamentales:
- Orden: Un número natural \(a\) es menor que un número \(b\) (\(a < b\)) si y sólo si el conjunto \(a\) es un elemento del conjunto \(b\) (\(a \in b\)).
- Estructura de Conjuntos: Cada número natural es un conjunto bien ordenado por la relación de pertenencia.
🧐 Axiomas de Peano
Esta construcción satisface los axiomas de Peano, que formalizan las propiedades intuitivas de los números naturales:
- El \(0\) es un número natural.
- Si \(n\) es un número natural, su sucesor \(S(n)\) también lo es.
- El \(0\) no es el sucesor de ningún número natural.
- Si dos números naturales tienen el mismo sucesor, entonces son el mismo número (Si \(S(a) = S(b)\), entonces \(a = b\)).
- Principio de Inducción Matemática: Si una propiedad es cierta para el 0, y si el hecho de que sea cierta para un número \(n\) implica que también es cierta para su sucesor \(S(n)\), entonces la propiedad es cierta para todos los números naturales.
Conclusión
Esta construcción de los números naturales utilizando conjuntos y el vacío es uno de los pilares de las matemáticas modernas. A partir de estas definiciones formales, es posible construir rigurosamente todo el sistema numérico, incluyendo los números enteros, racionales, reales y complejos, asegurando que toda la aritmética descanse sobre una base lógica sólida.
3. Propiedades de los números naturales
Los Números Naturales: Más que solo contar
Los números naturales, esos que usamos para contar (1, 2, 3...), son mucho más que simples herramientas para enumerar objetos. Tienen una estructura matemática rica y fascinante. ¡Vamos a explorarla!
¿Qué son los números naturales?
Los números naturales son aquellos que usamos intuitivamente para contar objetos o para indicar el orden en una secuencia. El conjunto de los números naturales se representa con la letra \( \mathbb{N} \).
Más allá de contar: El semianillo
En matemáticas, los números naturales junto con las operaciones de suma y multiplicación forman una estructura llamada semianillo. ¿Qué significa esto?
Un semianillo es como un "anillo a medio camino". Tiene las operaciones de suma y multiplicación con muchas de las propiedades que ya conoces (asociativa, conmutativa, distributiva). La gran diferencia con estructuras más completas como los "anillos" (donde trabajan los números enteros \( \mathbb{Z} \)) es que en un semianillo no se exige que cada número tenga un inverso aditivo (por ejemplo, en los naturales, no existe un número que al sumarlo a 5 dé 0). Es la estructura fundamental que nos permite operar.
Propiedades de la suma:
- Asociativa: No importa cómo agrupemos los números, el resultado es el mismo. \( (a + b) + c = a + (b + c) \)
- Conmutativa: El orden de los sumandos no altera la suma. \( a + b = b + a \)
- Elemento neutro: Existe el 0, que al sumarlo a cualquier número no lo modifica. \( a + 0 = a \)
Ejercicios sobre la suma:
- Calcula: \( (15 + 8) + 23 \) y \( 15 + (8 + 23) \). ¿Qué propiedad se cumple?
- ¿Es cierto que \( 34 + 56 = 56 + 34 \)? Justifica tu respuesta.
- Encuentra el valor de \( x \) que satisface la ecuación \( x + 12 = 35 \).
- Respuesta: \( (15 + 8) + 23 = 23 + 23 = 46 \). Y \( 15 + (8 + 23) = 15 + 31 = 46 \). Se cumple la propiedad asociativa.
- Respuesta: Sí, es cierto. \( 34 + 56 = 90 \) y \( 56 + 34 = 90 \). Esto se debe a la propiedad conmutativa.
- Respuesta: Para despejar \(x\), restamos 12 a ambos lados: \( x = 35 - 12 \), por lo que \( x = 23 \).
Propiedades de la multiplicación:
- Asociativa: La agrupación de los factores no cambia el resultado. \( (a \cdot b) \cdot c = a \cdot (b \cdot c) \)
- Elemento neutro: Existe el 1, que al multiplicarlo por cualquier número no lo altera. \( a \cdot 1 = a \)
Ejercicios sobre la multiplicación:
- Verifica si se cumple la propiedad asociativa en la siguiente operación: \( (4 \cdot 7) \cdot 9 = 4 \cdot (7 \cdot 9) \).
- ¿Cuál es el resultado de multiplicar cualquier número natural por 1? Da un ejemplo.
- Resuelve la ecuación \( 3 \cdot y = 27 \).
- Respuesta: \( (4 \cdot 7) \cdot 9 = 28 \cdot 9 = 252 \). Y \( 4 \cdot (7 \cdot 9) = 4 \cdot 63 = 252 \). Sí se cumple la propiedad asociativa.
- Respuesta: El resultado es el mismo número natural. Esto es por la propiedad del elemento neutro multiplicativo. Ejemplo: \( 159 \cdot 1 = 159 \).
- Respuesta: Para despejar \(y\), dividimos ambos lados por 3: \( y = \frac{27}{3} \), por lo que \( y = 9 \).
Propiedad distributiva:
La multiplicación se "distribuye" sobre la suma:
\( a \cdot (b + c) = (a \cdot b) + (a \cdot c) \)
Ejercicios sobre la propiedad distributiva:
- Aplica la propiedad distributiva para calcular \( 5 \cdot (8 + 2) \).
- Escribe la siguiente expresión usando la propiedad a la inversa (factorizando): \( 3 \cdot 9 + 3 \cdot 4 \).
- Resuelve: \( 6 \cdot (10 - 4) \) utilizando la propiedad distributiva.
- Respuesta: \( 5 \cdot (8 + 2) = (5 \cdot 8) + (5 \cdot 2) = 40 + 10 = 50 \).
- Respuesta: Identificamos el factor común, que es 3. Luego agrupamos los otros términos: \( 3 \cdot (9 + 4) \).
- Respuesta: \( 6 \cdot (10 - 4) = (6 \cdot 10) - (6 \cdot 4) = 60 - 24 = 36 \).
El último ejercicio usa la resta. Aunque la propiedad distributiva también funciona aquí, es importante recordar que la resta no es una operación interna en \( \mathbb{N} \). Es decir, el resultado de una resta no siempre es un número natural (ej: \(4 - 10\)). ¡Este tema lo retomaremos cuando estudiemos los números enteros \( \mathbb{Z} \)!
Otras características importantes
Conjunto bien ordenado
Esto significa que cualquier conjunto de números naturales (por ejemplo, \( \{5, 12, 8\} \) ) siempre tiene un número que es el más pequeño de todos (en este caso, el 5).
La propiedad de ser un "conjunto bien ordenado" es más poderosa de lo que parece. Significa que no importa qué subconjunto de números naturales elijas (¡incluso uno infinito!), siempre podrás encontrar un primer elemento. Esto nos da un "punto de partida" garantizado, lo que es fundamental para el principio de inducción matemática.
Axiomas de Peano
Los números naturales se construyen a partir de un conjunto de axiomas, llamados Axiomas de Peano. Son las reglas del juego.
- \( 0 \) es un número natural.
- Todo número natural \( n \) tiene un sucesor, \( S(n) \), que también es un número natural.
- \( 0 \) no es el sucesor de ningún número natural.
- Si dos números naturales tienen el mismo sucesor, entonces son iguales. (Si \( S(n) = S(m) \), entonces \( n = m \)).
- Principio de inducción matemática: Si una propiedad es cierta para el 0, y si al ser cierta para un número \(n\) también lo es para su sucesor \(S(n)\), entonces es cierta para todos los números naturales.
En resumen
Los números naturales, aunque parezcan simples, esconden una estructura matemática compleja y fascinante. Son la base de la aritmética y de muchas otras ramas de las matemáticas.
4. Adición y Sustracción de Números Naturales
Algoritmo de la Adición de Números Naturales
El algoritmo de la adición es un procedimiento sistemático para sumar dos o más números, basándose en el valor posicional de nuestro sistema de numeración decimal.
- Alinear los números: Escribe los números uno debajo del otro, asegurando que las unidades, decenas, centenas, etc., queden en la misma columna.
- Sumar columna por columna (de derecha a izquierda): Empieza por las unidades. Suma todos los dígitos de esa columna.
- Anotar y llevar (si es necesario): Si la suma de una columna es 10 o más, anota la cifra de la unidad del resultado debajo de la columna y "llevas" la cifra de la decena a la columna siguiente (la de la izquierda), sumándola en el próximo paso.
- Repetir: Continúa este proceso con todas las columnas hasta terminar.
⚠️ ¡Un Error Típico!
❌ Error: Empezar a sumar por la izquierda (por las columnas de mayor valor).
✔️ Correcto: Recuerda que siempre sumamos de derecha a izquierda (unidades, luego decenas, etc.). Esto es fundamental para poder "llevar" o "acarrear" las reservas correctamente. ¡El valor posicional es la clave!
Ejemplo con reserva: 345 + 187
Vamos a aplicar el algoritmo:
- Unidades: \(5 + 7 = 12\). Escribimos el 2 y llevamos 1 a las decenas.
- Decenas: \(4 + 8 + \color{blue}{1} \text{ (que llevábamos)} = 13\). Escribimos el 3 y llevamos 1 a las centenas.
- Centenas: \(3 + 1 + \color{red}{1} \text{ (que llevábamos)} = 5\). Escribimos el 5.
Resultado: \(345 + 187 = 532\)
Ejercicios de Adición
Sin Reserva
- 25 + 13
- 142 + 56
- 2000 + 500 + 25
- 105 + 234
- Respuesta: 38
- Respuesta: 198
- Respuesta: 2525
- Respuesta: 339
Con Reserva
- 38 + 9
- 567 + 89
- 1234 + 567
- 99 + 1
- 456 + 789 + 123
- 18 + 27 + 36 + 45
- Respuesta: 47
- Respuesta: 656
- Respuesta: 1801
- Respuesta: 100
- Respuesta: 1368
- Respuesta: 126
Algoritmo de la Sustracción de Números Naturales
El algoritmo de la sustracción con canje (o "pedir prestado") es el procedimiento que usamos para restar cuando una cifra en el número de arriba (minuendo) es menor que la de abajo (sustraendo).
- Alinear los números: El minuendo arriba y el sustraendo abajo, bien alineados por columnas.
- Restar columna por columna (de derecha a izquierda): Empieza por las unidades.
- Verificar y canjear (si es necesario): Si el dígito de arriba es menor que el de abajo, "pide prestado" 1 al dígito de la columna de la izquierda. Ese 1 se convierte en 10 en la columna actual. El dígito al que le pediste prestado disminuye en 1.
- Restar y repetir: Realiza la resta en la columna y continúa el proceso con las demás columnas hasta terminar.
⚠️ ¡Un Error Típico!
❌ Error: Empezar a restar por la izquierda o restar "el de abajo menos el de arriba" (ej. en 52-17, hacer 7-2 en la columna de unidades).
✔️ Correcto: Siempre restamos de derecha a izquierda y siempre es "el dígito de arriba menos el de abajo". Si el de arriba es más pequeño, es obligatorio "pedir prestado" o hacer un canje.
Ejemplo con canje: 532 - 285
- Unidades: A 2 no le puedo quitar 5. Pido prestado 1 a las decenas. El 3 se convierte en 2, y el 2 en 12. Ahora, \(12 - 5 = 7\).
- Decenas: Al 2 (que antes era un 3) no le puedo quitar 8. Pido prestado 1 a las centenas. El 5 se convierte en 4, y el 2 en 12. Ahora, \(12 - 8 = 4\).
- Centenas: \(4 - 2 = 2\).
Resultado: \(532 - 285 = 247\)
El canje sobre un cero puede ser confuso. Piensa que vas a la "columna vecina" a pedir una decena. Si esa vecina no tiene (es un 0), ella tiene que ir a su propia vecina (la de más a la izquierda) a pedir primero. Es como un favor en cadena. Por eso en 1200 - 17, las centenas (2) le prestan a las decenas (0), y solo entonces las decenas le pueden prestar a las unidades.
Ejemplo con doble canje: 1200 - 17
Este es un caso especial donde debemos "pedir prestado" a través de un cero.
- Unidades: A 0 no le puedo quitar 7. Necesito pedir prestado a la columna de las decenas.
- Canje en Cascada: La columna de las decenas también es un 0, así que no puede prestar. Vamos a la columna de las centenas, que tiene un 2.
- El 2 de las centenas presta 1 y se convierte en 1.
- Ese 1 que prestó se convierte en 10 decenas. Ahora la columna de las decenas tiene un 10.
- Canje Final: Ahora que las decenas tienen un 10, sí pueden prestarle a las unidades.
- El 10 de las decenas presta 1 y se convierte en 9.
- Ese 1 que prestó se convierte en 10 unidades. La columna de las unidades ahora tiene un 10.
- Realizar las restas (finalmente):
- Unidades: \(10 - 7 = 3\)
- Decenas: \(9 - 1 = 8\)
- Centenas: \(1 - 0 = 1\)
- Unidades de mil: \(1 - 0 = 1\)
Resultado: \(1200 - 17 = 1183\)
Un excelente truco para verificar si tu resta está correcta es usar la suma. La resta es la operación inversa de la suma. Si calculaste que \(a - b = c\), entonces siempre se debe cumplir que ¡\(b + c = a\)! Por ejemplo, para comprobar que \(532 - 285 = 247\), simplemente suma \(285 + 247\). ¡El resultado debe ser 532!
Ejercicios de Sustracción
Sin Canje
- 48 - 23
- 165 - 42
- 345 - 123
- 75 - 45
- Respuesta: 25
- Respuesta: 123
- Respuesta: 222
- Respuesta: 30
Con Canje
- 72 - 8
- 5000 - 2500
- 678 - 90
- 2345 - 678
- 100 - 1
- 131 - 75 - 44
- Respuesta: 64
- Respuesta: 2500
- Respuesta: 588
- Respuesta: 1667
- Respuesta: 99
- Respuesta: 12 (Se resuelve de izquierda a derecha: primero 131 - 75 = 56, y luego 56 - 44 = 12).
Estos algoritmos no son solo para el colegio. Los usas todos los días casi sin darte cuenta: al calcular el vuelto en una compra, al llevar la cuenta de los puntos en un juego, o al medir ingredientes para una receta. ¡Dominar la suma y la resta te hace la vida más fácil!
5. Multiplicación de Números Naturales
Multiplicación de Números Naturales
La multiplicación es una operación matemática que, en su forma más simple, puede considerarse como una suma repetida. El resultado de multiplicar dos números se llama producto, y los números que se multiplican se llaman factores.
Propiedades de la Multiplicación
- Conmutativa: El orden de los factores no altera el producto. \(a \times b = b \times a\)
- Asociativa: La forma en que se agrupan los factores no altera el producto. \((a \times b) \times c = a \times (b \times c)\)
- Elemento Neutro: El uno (1) es el elemento neutro de la multiplicación. \(a \times 1 = a\)
- Distributiva: La multiplicación se distribuye sobre la suma. \(a \times (b + c) = (a \times b) + (a \times c)\)
- Factor Cero: Cualquier número multiplicado por cero da como resultado cero. \(a \times 0 = 0\)
Algoritmo de la Multiplicación
Nivel 1: Un factor de un dígito
Aquí multiplicaremos un número de varios dígitos por uno de un solo dígito.
⚠️ ¡Atención al Orden!
❌ Error: Empezar a multiplicar por la izquierda.
✔️ Correcto: Al igual que en la suma y resta, siempre empezamos por la derecha (las unidades) y avanzamos hacia la izquierda. Esto es crucial para manejar las reservas correctamente.
Ejemplo: \(153 \times 3\)
\[ \begin{array}{rrrrrr} & 1 & & & & \\ & 1 & 5 & 3 & \times & 3 \\ \hline & 4 & 5 & 9 \\ \end{array} \]
La multiplicación se hace de derecha a izquierda:
- \(3 \times 3 = 9\).
- \(3 \times 5 = 15\). Se anota el 5 y se guarda 1 centena de reserva (se anota arriba de la columna de las centenas).
- \(3 \times 1 = 3\). A estas 3 centenas se le suma la reserva: \(3 + 1 = 4\).
Ejercicios Nivel 1
- \(5 \times 3\)
- \(12 \times 4\)
- \(34 \times 2\)
- \(123 \times 3\)
- \(245 \times 5\)
- \(567 \times 8\)
- \(1234 \times 6\)
- \(4567 \times 9\)
- \(7890 \times 7\)
- \(9876 \times 1\)
- Respuesta: 15
- Respuesta: 48
- Respuesta: 68
- Respuesta: 369
- Respuesta: 1225
- Respuesta: 4536
- Respuesta: 7404
- Respuesta: 41103
- Respuesta: 55230
- Respuesta: 9876
Nivel 2: Ambos factores de dos o más dígitos
El procedimiento se expande. Multiplicamos el primer factor por cada dígito del segundo factor, respetando su valor posicional.
Cuando multiplicas por el dígito de las decenas, en realidad estás multiplicando por 10, 20, 30, etc. Correr un espacio hacia la izquierda (o agregar un cero al final) es el truco que usamos para asegurarnos de que el resultado refleje ese valor posicional. Si multiplicas por las centenas, corres dos espacios, y así sucesivamente.
Ejemplo: \(56 \times 42\)
\[ \begin{array}{ccccccc} & & 5 & 6 & \times & \color{blue}{4} & \color{red}{2} \\ \hline & \color{red}{1} & \color{red}{1} & \color{red}{2} & & & \\ \color{blue}{2} & \color{blue}{2} & \color{blue}{4} & \color{green}{0} & & & \\ \hline 2 & 3 & 5 & 2 & & &\\ \end{array} \]
- Se multiplica 56 por 2 (unidades del segundo factor), resultando 112.
- Se multiplica 56 por 4 (decenas del segundo factor), resultando 224. Como son decenas, se le agrega un cero al final (2240).
- Se suman ambos productos: 112 + 2240 = 2352.
Ejercicios Nivel 2 y 3
- \(12 \times 23\)
- \(34 \times 15\)
- \(78 \times 69\)
- \(99 \times 99\)
- \(123 \times 321\)
- \(456 \times 654\)
- \(789 \times 987\)
- \(102 \times 405\)
- \(5678 \times 1234\)
- \(1111 \times 1111\)
- Respuesta: 276
- Respuesta: 510
- Respuesta: 5382
- Respuesta: 9801
- Respuesta: 39483
- Respuesta: 298224
- Respuesta: 778743
- Respuesta: 41310
- Respuesta: 7006652
- Respuesta: 1234321
Resolución de Problemas
Para identificar si un problema se resuelve con una multiplicación, busca pistas que indiquen una suma de grupos iguales o una cantidad que se repite. Palabras clave como:
- "Veces", "doble", "triple"...
- "Producto de..."
- "Cada caja tiene...", "cada fila tiene..."
- Cálculo de áreas de rectángulos.
Problemas de Aplicación
- En una caja hay 12 chocolates. ¿Cuántos chocolates habrá en 5 cajas iguales?
- Un edificio tiene 7 pisos. Si cada piso tiene 4 departamentos, ¿cuántos departamentos hay en el edificio?
- María tiene 3 álbumes de fotos. Si cada álbum tiene 25 fotos, ¿cuántas fotos tiene María en total?
- Un auto recorre 60 kilómetros por hora. ¿Cuántos kilómetros recorrerá en 3 horas?
- Si una entrada al cine cuesta $2.500, ¿cuánto costarán 4 entradas?
- En una sala de clases hay 8 filas con 12 asientos en cada fila. ¿Cuántos asientos hay en total?
- Un paquete trae 6 galletas. ¿Cuántas galletas habrán en 9 paquetes?
- Un libro tiene 250 páginas. Si leo 5 páginas por día, ¿cuántas páginas leeré en una semana (7 días)?
- Un agricultor cosecha 4 sacos de papas al día. Si cada saco pesa 50 kilos, ¿cuántos kilos de papas cosecha en 6 días?
- El corazón de una persona late aproximadamente 70 veces por minuto. ¿Cuántas veces late en 15 minutos?
- Respuesta: \(12 \times 5 = 60\) chocolates.
- Respuesta: \(7 \times 4 = 28\) departamentos.
- Respuesta: \(3 \times 25 = 75\) fotos.
- Respuesta: \(60 \times 3 = 180\) kilómetros.
- Respuesta: \(2500 \times 4 = 10000\) pesos.
- Respuesta: \(8 \times 12 = 96\) asientos.
- Respuesta: \(6 \times 9 = 54\) galletas.
- Respuesta: \(5 \times 7 = 35\) páginas. (Ojo: el total de páginas del libro es información distractora).
- Respuesta: \((4 \times 50) \times 6 = 200 \times 6 = 1200\) kilos.
- Respuesta: \(70 \times 15 = 1050\) latidos.
6. División de Números Naturales
División de Números Naturales
La división es una operación que consiste en repartir una cantidad en partes iguales. El número a repartir se llama dividendo, el número de partes es el divisor, el resultado es el cociente y lo que sobra es el resto o residuo.
Propiedades de la División
- No es Conmutativa: El orden importa. \(10 \div 2\) no es lo mismo que \(2 \div 10\).
- No es Asociativa: No se pueden agrupar de cualquier forma. \((20 \div 4) \div 2\) no es lo mismo que \(20 \div (4 \div 2)\).
- Elemento Neutro: Cualquier número dividido entre 1 da el mismo número (\(a \div 1 = a\)).
- División por sí mismo: Un número (distinto de cero) dividido por sí mismo es 1 (\(a \div a = 1\)).
⚠️ ¡Prohibido Dividir por Cero!
En las matemáticas que usamos en el colegio, la división por cero no está definida. No se puede repartir una cantidad en cero partes. ¡Es una regla fundamental!
Ejercicios de División
Nivel 1: Divisores de un dígito (sin resto)
En este nivel, las divisiones serán exactas (resto cero).
Ejemplo: 46815 ÷ 5
\[ \begin{array}{cccccc|l} \color{blue}{4} & \color{blue}{6'} & \color{blue}{8'} & \color{blue}{1'} & \color{blue}{5'} & : \fbox{5} =\color{purple}{9}\color{red}{3}\color{magenta}{6}\color{red}{3} & Tabla.del.5 \\ \hline \color{purple}{-4} & \color{purple}{5} & & & & & \color{gray}{5 \bullet 1 =5}\\ & \color{pink}{1} & \color{blue}{8} & & & & \color{gray}{5 \bullet 2 =10}\\ & \color{red}{-1} & \color{red}{5} & & & & \color{red}{5 \bullet 3 =15}\\ & & \color{pink}{3} & \color{blue}{1} & & & \color{gray}{5 \bullet 4 =20}\\ & & \color{magenta}{-3} & \color{magenta}{0} & & & \color{gray}{5 \bullet 5 =25}\\ & & & \color{pink}{1} & \color{blue}{5} & & \color{magenta}{5 \bullet 6 =30}\\ & & & \color{red}{1} & \color{red}{5} & & \color{gray}{5 \bullet 7 =35}\\ & & & & 0 & & \color{gray}{5 \bullet 8 =40}\\ & & & & & & \color{purple}{5 \bullet 9 =45}\\ \end{array} \]
Explicación del procedimiento:
- Como 4 es menor que 5, tomamos 46. En la tabla del 5, lo más cercano es \(5 \times 9 = 45\). Anotamos 9 en el cociente. Restamos \(46 - 45 = 1\).
- Bajamos el 8, formando 18. En la tabla del 5, lo más cercano es \(5 \times 3 = 15\). Anotamos 3 en el cociente. Restamos \(18 - 15 = 3\).
- Bajamos el 1, formando 31. Lo más cercano es \(5 \times 6 = 30\). Anotamos 6 en el cociente. Restamos \(31 - 30 = 1\).
- Bajamos el 5, formando 15. Exactamente \(5 \times 3 = 15\). Anotamos 3 en el cociente. Restamos \(15 - 15 = 0\).
Resultado: Cociente 9363, Resto 0.
Ejercicios Nivel 1
- \(6 \div 2\)
- \(15 \div 3\)
- \(24 \div 4\)
- \(125 \div 5\)
- \(248 \div 8\)
- \(369 \div 3\)
- \(1234 \div 2\)
- \(4563 \div 3\)
- \(7895 \div 5\)
- \(9876 \div 6\)
- Respuesta: 3
- Respuesta: 5
- Respuesta: 6
- Respuesta: 25
- Respuesta: 31
- Respuesta: 123
- Respuesta: 617
- Respuesta: 1521
- Respuesta: 1579
- Respuesta: 1646
Nivel 2: Divisores de un dígito (con resto)
En este nivel, las divisiones pueden tener un resto distinto de cero.
Ejemplo de División con Resto: 1659 ÷ 8
\[ \begin{array}{ccccc|l} \color{blue}{1} & \color{blue}{6'} & \color{blue}{5'} & \color{blue}{9'} & : \fbox{8} = \color{purple}{2}\color{red}{0}\color{magenta}{7} & \text{Tabla del 8} \\ \hline \color{purple}{-1} & \color{purple}{6} & & & & \color{gray}{8 \times 1 = 8} \\ & \color{pink}{0} & \color{blue}{5} & & & \color{purple}{8 \times 2 = 16} \\ & \color{red}{-0} & \color{red}{0} & & & \color{gray}{8 \times 3 = 24} \\ & & \color{pink}{5} & \color{blue}{9} & & \color{gray}{8 \times 4 = 32} \\ & & \color{magenta}{-5} & \color{magenta}{6} & & \color{gray}{8 \times 5 = 40} \\ & & & \color{green}{3} & & \color{gray}{8 \times 6 = 48} \\ & & & & & \color{magenta}{8 \times 7 = 56} \\ & & & & & \color{gray}{8 \times 8 = 64} \\ & & & & & \color{gray}{8 \times 9 = 72} \\ \end{array} \]
Explicación:
- Tomamos 16. En la tabla del 8, \(8 \times 2 = 16\). Anotamos 2 en el cociente. Restamos \(16 - 16 = 0\).
- Bajamos el 5. Como 5 es menor que 8, el múltiplo que sirve es \(8 \times 0 = 0\). Anotamos 0 en el cociente. Restamos \(5 - 0 = 5\).
- Bajamos el 9, formando 59. El múltiplo más cercano es \(8 \times 7 = 56\). Anotamos 7 en el cociente. Restamos \(59 - 56 = 3\).
Resultado: Cociente 207, Resto 3.
Para saber si una división está correcta, usa esta fórmula:
Dividendo = (Divisor × Cociente) + Resto.
Si el resultado coincide con tu dividendo original, ¡la división está perfecta!
Ejercicios Nivel 2
- \(7 \div 2\)
- \(16 \div 3\)
- \(27 \div 4\)
- \(128 \div 5\)
- \(250 \div 8\)
- \(370 \div 3\)
- \(1235 \div 2\)
- \(4568 \div 3\)
- \(7896 \div 5\)
- \(9875 \div 6\)
- Respuesta: 3 Resto 1
- Respuesta: 5 Resto 1
- Respuesta: 6 Resto 3
- Respuesta: 25 Resto 3
- Respuesta: 31 Resto 2
- Respuesta: 123 Resto 1
- Respuesta: 617 Resto 1
- Respuesta: 1522 Resto 2
- Respuesta: 1579 Resto 1
- Respuesta: 1645 Resto 5
Nivel 3: Divisores de dos dígitos
El procedimiento es el mismo, pero ahora estimamos con la tabla de un número de dos dígitos.
Ejemplo: 1693 ÷ 12
\[ \begin{array}{ccccc|c} \color{blue}{1} & \color{blue}{6'} & \color{blue}{9'} & \color{blue}{3'} & : \fbox{12} = \color{magenta}{1}\color{red}{4}\color{magenta}{1} & \text{Tabla del 12} \\ \hline \color{magenta}{-1} & \color{magenta}{2} && & &\color{magenta}{ 12 \bullet 1 = 12}\\ & \color{pink}{4} & \color{blue}{9} & && \color{gray}{12 \bullet 2 = 24}\\ & \color{red}{-4} & \color{red}{8} && & \color{gray}{12 \bullet 3 = 36}\\ & & \color{pink}{1} & \color{blue}{3} &&\color{red}{ 12 \bullet 4 = 48}\\ && \color{magenta}{-1} & \color{magenta}{2} & & \color{gray}{12 \bullet 5 = 60}\\ & &&\color{green}{1} & & \color{gray}{\dots} \\ \end{array} \]
Explicación:
- Tomamos 16. El múltiplo de 12 que más se acerca es \(12 \times 1 = 12\). Anotamos 1 en el cociente. Restamos \(16 - 12 = 4\).
- Bajamos el 9, formando 49. El múltiplo más cercano es \(12 \times 4 = 48\). Anotamos 4 en el cociente. Restamos \(49 - 48 = 1\).
- Bajamos el 3, formando 13. El más cercano es \(12 \times 1 = 12\). Anotamos 1 en el cociente. Restamos \(13 - 12 = 1\).
Resultado: Cociente 141, Resto 1.
Ejercicios Nivel 3
- \(123 \div 12\)
- \(456 \div 24\)
- \(789 \div 32\)
- \(1024 \div 16\)
- \(5678 \div 45\)
- \(9876 \div 78\)
- \(1000 \div 25\)
- \(2468 \div 57\)
- \(9753 \div 86\)
- \(1111 \div 11\)
- Respuesta: 10 Resto 3
- Respuesta: 19
- Respuesta: 24 Resto 21
- Respuesta: 64
- Respuesta: 126 Resto 8
- Respuesta: 126 Resto 48
- Respuesta: 40
- Respuesta: 43 Resto 17
- Respuesta: 113 Resto 35
- Respuesta: 101
Nivel 4: Divisores de tres o más dígitos
El procedimiento no cambia, pero requiere más cálculo y estimación.
Ejercicios Nivel 4
- \(5678 \div 123\)
- \(9876 \div 456\)
- \(12345 \div 789\)
- \(24680 \div 102\)
- \(13579 \div 246\)
- \(86420 \div 975\)
- \(11111 \div 111\)
- \(99999 \div 333\)
- \(10000 \div 456\)
- \(88888 \div 222\)
- Respuesta: 46 Resto 20
- Respuesta: 21 Resto 300
- Respuesta: 15 Resto 510
- Respuesta: 241 Resto 98
- Respuesta: 55 Resto 49
- Respuesta: 88 Resto 620
- Respuesta: 100 Resto 11
- Respuesta: 300 Resto 99
- Respuesta: 21 Resto 424
- Respuesta: 400 Resto 88
Resolución de Problemas con División
La división responde principalmente a dos grandes preguntas: repartir en partes iguales o averiguar cuántas veces cabe una cantidad en otra. Busca estas pistas en los problemas:
- Términos de reparto: "Repartir", "distribuir", "compartir", "a cada uno le tocan...", etc.
- Términos de agrupamiento: "¿Cuántos grupos se pueden formar?" o la pregunta directa "¿cuántas veces cabe?".
- Fracciones de un todo: "Calcular la mitad", "la tercera parte", "la cuarta parte", etc.
- Palabras directas: A veces el problema usará los términos matemáticos exactos como "dividir" o "el cociente de...".
Problemas de Aplicación
- Se quieren repartir 48 chocolates entre 6 amigos en partes iguales. ¿Cuántos chocolates le tocan a cada uno?
- Un padre quiere repartir $100 entre sus 4 hijos. ¿Cuánto dinero le corresponde a cada uno?
- En una escuela hay 240 estudiantes. Si se quieren formar equipos de 8 estudiantes, ¿cuántos equipos se pueden formar?
- Un libro tiene 360 páginas. Si quiero leer el libro en 12 días, leyendo la misma cantidad cada día, ¿cuántas páginas debo leer por día?
- Se compraron 50 metros de tela para hacer 10 vestidos iguales. ¿Cuánta tela se usará para cada vestido?
- Un agricultor cosechó 729 manzanas y quiere guardarlas en cajas. Si en cada caja caben 9 manzanas, ¿cuántas cajas necesita?
- Una fábrica produjo 7500 juguetes en una semana laboral de 5 días. Si cada día se fabricó la misma cantidad, ¿cuántos juguetes se produjeron por día?
- Un avión recorre 2400 kilómetros en 3 horas a velocidad constante. ¿Cuántos kilómetros recorre por hora?
- Se quieren repartir 96 galletas entre un grupo de niños. Si a cada niño le tocan 8 galletas, ¿cuántos niños hay en el grupo?
- María tiene ahorrado $3.600 y quiere comprar libros que cuestan $900 cada uno. ¿Cuántos libros puede comprar?
- Respuesta: \(48 \div 6 = 8\) chocolates.
- Respuesta: \(100 \div 4 = 25\) pesos.
- Respuesta: \(240 \div 8 = 30\) equipos.
- Respuesta: \(360 \div 12 = 30\) páginas.
- Respuesta: \(50 \div 10 = 5\) metros.
- Respuesta: \(729 \div 9 = 81\) cajas.
- Respuesta: \(7500 \div 5 = 1500\) juguetes.
- Respuesta: \(2400 \div 3 = 800\) kilómetros por hora.
- Respuesta: \(96 \div 8 = 12\) niños.
- Respuesta: \(3600 \div 900 = 4\) libros.
7. Criterios de Divisibilidad: ¡Atajos Matemáticos!
Criterios de Divisibilidad: ¡Atajos Matemáticos!
¿Alguna vez te has preguntado si un número se puede dividir por otro de forma exacta sin tener que hacer la división completa? ¡Los criterios de divisibilidad son la respuesta! Son reglas o "atajos" que nos permiten saberlo solo con observar las cifras de un número.
- Un número es divisible por 2 si su última cifra es par (0, 2, 4, 6, 8).
- Un número es divisible por 3 si la suma de sus cifras es un múltiplo de 3.
- Un número es divisible por 4 si el número formado por sus dos últimas cifras es un múltiplo de 4.
- Un número es divisible por 5 si termina en 0 o en 5.
- Un número es divisible por 10 si termina en 0.
- Divisibilidad por 6: Un número es divisible por 6 si cumple los criterios del 2 y del 3 al mismo tiempo. Es decir, debe ser par y la suma de sus cifras debe ser múltiplo de 3.
- Divisibilidad por 7: Separa la última cifra, multiplícala por 2 y resta este resultado del número que quedó. Si el resultado es 0 o un múltiplo de 7, el número original es divisible por 7.
Ejemplo: Para 343 -> 34 - (3×2) = 28. Como 28 es múltiplo de 7, 343 también lo es. - Divisibilidad por 8: Un número es divisible por 8 si el número formado por sus tres últimas cifras es un múltiplo de 8.
- Divisibilidad por 9: Un número es divisible por 9 si la suma de sus cifras es un múltiplo de 9.
- Divisibilidad por 11: Suma las cifras en posiciones impares por un lado y las de posiciones pares por otro. Resta los resultados. Si la diferencia es 0 o un múltiplo de 11, el número es divisible por 11.
Ejemplo: Para 918.082 -> Posiciones impares (9+8+8) = 25. Posiciones pares (1+0+2) = 3. La resta es 25 - 3 = 22. Como 22 es múltiplo de 11, 918.082 es divisible por 11.
¡Pon a prueba tus conocimientos!
Indica por cuáles de estos números (2, 3, 4, 5, 6, 7, 8, 9, 10, 11) son divisibles las siguientes cantidades.
- 234
- 840
- 495
- 1.372
- 7.040
- 2.915
- 3.333
- 6.182
- 9.009
- 12.321
- 45.678
- 55.440
| Número | Es divisible por... |
|---|---|
| 234 | 2, 3, 6, 9 |
| 840 | 2, 3, 4, 5, 6, 7, 8, 10 |
| 495 | 3, 5, 9, 11 |
| 1.372 | 2, 4, 7 |
| 7.040 | 2, 4, 5, 8, 10, 11 |
| 2.915 | 5 |
| 3.333 | 3, 11 |
| 6.182 | 2 |
| 9.009 | 3, 7, 9, 11 |
| 12.321 | 3, 9 |
| 45.678 | 2, 3, 6 |
| 55.440 | 2, 3, 4, 5, 6, 8, 10, 11 |
Los criterios de divisibilidad no son magia. Se basan en las propiedades de nuestro sistema de numeración decimal (base 10). Investigar la demostración de cada criterio puede ser un desafío matemático muy interesante. ¡Anímate a buscarlo!
8. ¡Explorando el Mundo de los Números Primos!
¡Explorando el Mundo de los Números Primos!
Imagina que los números son como bloques de construcción. ¡Algunos son piezas únicas y fundamentales! Esos bloques especiales se llaman números primos.
- Un número primo es un número natural mayor que 1 que solo tiene dos divisores distintos: el 1 y sí mismo. (Ej: 2, 3, 5, 7, 11)
- Un número compuesto es aquel que tiene más de dos divisores. (Ej: 4, 6, 8, 9, 10)
- Ojo: El número 1 no se considera ni primo ni compuesto.
Ejemplos para entender la diferencia
La clave está en contar cuántos divisores tiene un número. Usemos tu idea de los "divisores elementales" (que son siempre el 1 y el mismo número).
| ✅ Números Primos (Solo 2 divisores) | ❌ Números Compuestos (Más de 2 divisores) |
|---|---|
| Número 7 Divisores: {1, 7} Tiene solo los 2 divisores elementales. |
Número 9 Divisores: {1, 3, 9} Tiene los 2 elementales y otros más (en este caso, el 3). |
| Número 11 Divisores: {1, 11} Tiene solo los 2 divisores elementales. |
Número 12 Divisores: {1, 2, 3, 4, 6, 12} Tiene los 2 elementales y muchos otros más. |
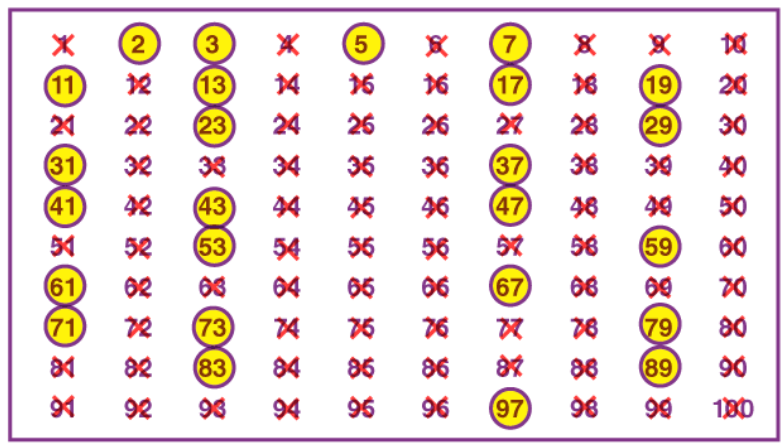
¡A cazar primos con la Criba de Eratóstenes!
La Criba de Eratóstenes es un método antiguo y muy visual para encontrar todos los números primos hasta un cierto límite. ¡Es como un juego de detectives!
- Escribe una lista de números, por ejemplo, del 1 al 50.
- Tacha el número 1, ya que no es primo.
- Encierra en un círculo el 2 (el primer primo) y tacha todos sus múltiplos (4, 6, 8...).
- Encierra el siguiente número no tachado (el 3) y tacha todos sus múltiplos (6, 9, 12...).
- Continúa este proceso hasta que todos los números estén encerrados o tachados.
Al final, ¡todos los números que quedaron encerrados son los primos!
Descomposición en Factores Primos
Los números primos son los "ladrillos" con los que se construyen todos los demás números. Cualquier número compuesto puede escribirse como un producto único de números primos. A esto se le llama descomposición o factorización prima.
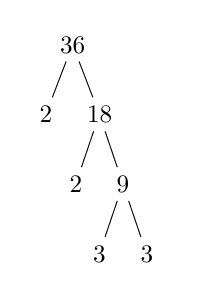
Ejemplo: Descomponer el número 36
Podemos hacerlo con divisiones sucesivas:
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
Entonces, la descomposición prima de 36 es: 2 x 2 x 3 x 3, que se escribe como \(2^2 \times 3^2\).
También podemos usar un árbol de factores:
¡Practica la factorización!
Ahora es tu turno. Intenta descomponer los siguientes números en factores primos:
- 48
- 75
- 120
- 160
- 392
- 48 = \(2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3\)
- 75 = \(3 \times 5 \times 5 = 3 \times 5^2\)
- 120 = \(2 \times 2 \times 2 \times 3 \times 5 = 2^3 \times 3 \times 5\)
- 160 = \(2 \times 2 \times 2 \times 2 \times 2 \times 5 = 2^5 \times 5\)
- 392 = \(2 \times 2 \times 2 \times 7 \times 7 = 2^3 \times 7^2\)
¿Por qué son importantes los números primos?
- Son los "ladrillos" de los números: Todo número compuesto tiene una "receta" única de factores primos (Teorema Fundamental de la Aritmética).
- Simplificación de fracciones: Conocer los factores primos de numerador y denominador es la clave para simplificar fracciones de forma eficiente.
- Criptografía: La seguridad en internet (contraseñas, transacciones bancarias) depende de operaciones con números primos extremadamente grandes.
Cuando envías un mensaje por WhatsApp o compras algo online, tu información se protege usando un sistema de llaves (pública y privada). La seguridad de este sistema se basa en que es muy fácil multiplicar dos números primos gigantes, pero es extremadamente difícil tomar el resultado (un número compuesto muy grande) y descubrir cuáles fueron los dos primos originales que lo formaron. ¡Las matemáticas protegen tus secretos!
9. Máximo Común Divisor (MCD): ¡Encontrando Conexiones!
Máximo Común Divisor (MCD): ¡Encontrando Conexiones!
El Máximo Común Divisor (MCD) de dos o más números es el número más grande que logra dividir a todos esos números de forma exacta, sin dejar residuo.
Imagina que tienes una cuerda de 12 metros y otra de 18 metros. Quieres cortarlas en trozos de igual longitud, pero que sean lo más largos posible y sin que sobre nada de cuerda.
El MCD te da la respuesta. El MCD(12, 18) = 6. Esto significa que:
- La longitud máxima de cada trozo es de 6 metros.
- De la cuerda de 12m, obtendrás \(12 \div 6 = 2\) trozos.
- De la cuerda de 18m, obtendrás \(18 \div 6 = 3\) trozos.
Cualquier medida más grande (por ejemplo, 7 metros) dejaría sobrantes. El MCD te da la máxima eficiencia.
Métodos para Calcular el MCD
1. Por Descomposición en Factores Primos
- Descomponer: Realiza la descomposición prima de cada número.
- Identificar: Busca los factores primos que se repiten (comunes) en todas las descomposiciones.
- Multiplicar: Multiplica esos factores comunes, usando siempre el menor exponente con el que aparecen.
Ejemplo: Calcular el MCD de 36 y 48
- Descomposición de 36: \(2 \times 2 \times 3 \times 3 = 2^2 \times 3^2\)
- Descomposición de 48: \(2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3^1\)
- Factores comunes: 2 y 3.
- Menor exponente del 2: Es 2 (de \(2^2\)).
- Menor exponente del 3: Es 1 (de \(3^1\)).
- Cálculo: MCD = \(2^2 \times 3^1 = 4 \times 3 = 12\).
Resultado: MCD(36, 48) = 12.
2. Algoritmo de Euclides
- Divide el número mayor por el menor.
- Toma el divisor y divídelo por el resto de la división anterior.
- Continúa dividiendo el último divisor por el último resto.
- Repite el proceso hasta que la división sea exacta (resto 0). El último divisor que usaste es el MCD.
Ejemplo: Calcular el MCD de 1071 y 462
- \(1071 \div 462 = 2\) con resto 147.
- Ahora dividimos el divisor anterior (462) por el resto (147):
\(462 \div 147 = 3\) con resto 21. - Repetimos el proceso:
\(147 \div 21 = 7\) con resto 0.
Como la última división fue exacta, el MCD es el último divisor que usamos.
Resultado: MCD(1071, 462) = 21.
¡A Practicar!
Ejercicios de Cálculo
Calcula el MCD de los siguientes números:
- 12 y 18
- 30 y 45
- 16, 24 y 40
- 75 y 125
- 28, 42 y 56
- 18, 27 y 36
- 120 y 150
- 36, 54 y 72
- 20, 30, 40 y 50
- 105, 140 y 175
- 60, 90, 120 y 150
- MCD(12, 18) = 6
- MCD(30, 45) = 15
- MCD(16, 24, 40) = 8
- MCD(75, 125) = 25
- MCD(28, 42, 56) = 14
- MCD(18, 27, 36) = 9
- MCD(120, 150) = 30
- MCD(36, 54, 72) = 18
- MCD(20, 30, 40, 50) = 10
- MCD(105, 140, 175) = 35
- MCD(60, 90, 120, 150) = 30
Problemas de Aplicación
- Un carpintero tiene dos tablas de madera, una de 120 cm y otra de 180 cm. Quiere cortarlas en trozos de igual longitud, lo más largos posible y sin desperdiciar madera. ¿Cuál es la mayor longitud posible de los trozos?
- Ana tiene 48 caramelos y 36 chocolates. Quiere repartirlos en bolsas de regalo, de modo que cada bolsa tenga la misma cantidad de caramelos y la misma cantidad de chocolates. ¿Cuál es el mayor número de bolsas que puede hacer?
- Un grupo de amigos quiere repartir 120 galletas y 150 caramelos en paquetes con la misma cantidad de cada golosina. ¿Cuál es el mayor número de paquetes que pueden hacer?
- En una frutería hay 72 manzanas, 96 naranjas y 60 plátanos. Se quieren colocar en cajas con la misma cantidad de cada fruta. ¿Cuál es el mayor número de cajas que se pueden llenar?
- Tres rollos de tela, uno de 140 metros, otro de 180 metros y otro de 210 metros, se quieren cortar en piezas de igual longitud, lo más largas posible y sin desperdiciar tela. ¿Cuál es la mayor longitud posible de las piezas?
- Un grupo de estudiantes quiere repartir 108 lápices, 84 bolígrafos y 60 gomas de borrar en estuches con la misma cantidad de cada artículo. ¿Cuál es el mayor número de estuches que pueden armar?
- Se tienen tres terrenos de 360, 480 y 600 metros cuadrados. Se quieren dividir en parcelas iguales de la mayor área posible. ¿Cuál será el área de cada parcela?
- Un grupo de niños quiere repartir 240 caramelos de fresa, 300 caramelos de limón y 180 caramelos de menta en bolsas con la misma cantidad de cada sabor. ¿Cuál es el mayor número de bolsas que pueden hacer?
- En una biblioteca hay 180 libros de historia, 120 libros de ciencias y 90 libros de literatura. Se quieren colocar en estantes con la misma cantidad de libros de cada tema. ¿Cuál es el mayor número de estantes que se pueden llenar?
- Se tienen cuatro cuerdas de 120 cm, 160 cm, 200 cm y 240 cm. Se quieren cortar en trozos de igual longitud, sin desperdiciar cuerda. ¿Cuál es la mayor longitud posible de los trozos?
- María tiene 60 caramelos de fresa, 75 caramelos de limón y 90 caramelos de naranja. Quiere repartirlos en bolsas con la misma cantidad de caramelos de cada sabor. ¿Cuál es el mayor número de bolsas que puede hacer?
- MCD(120, 180) = 60 cm.
- MCD(48, 36) = 12 bolsas.
- MCD(120, 150) = 30 paquetes.
- MCD(72, 96, 60) = 12 cajas.
- MCD(140, 180, 210) = 10 metros.
- MCD(108, 84, 60) = 12 estuches.
- MCD(360, 480, 600) = 120 metros cuadrados.
- MCD(240, 300, 180) = 60 bolsas.
- MCD(180, 120, 90) = 30 estantes.
- MCD(120, 160, 200, 240) = 40 cm.
- MCD(60, 75, 90) = 15 bolsas.
10. Mínimo Común Múltiplo (MCM): ¡Encontrando el Punto de Encuentro!
Mínimo Común Múltiplo (MCM): ¡Encontrando el Punto de Encuentro!
El Mínimo Común Múltiplo (MCM) de dos o más números es el número más pequeño (distinto de cero) que es múltiplo de todos ellos a la vez.
Imagina que dos autobuses salen de la misma estación. Uno sale cada 12 minutos y el otro cada 15 minutos. ¿En cuántos minutos volverán a coincidir en la estación?
- Múltiplos de 12: 12, 24, 36, 48, 60, 72...
- Múltiplos de 15: 15, 30, 45, 60, 75...
El primer múltiplo que tienen en común es 60. Por lo tanto, volverán a coincidir en 60 minutos. Matemáticamente: MCM(12, 15) = 60.
El MCM es muy útil para planificar horarios, resolver problemas de coincidencias y, sobre todo, para sumar o restar fracciones con distinto denominador.
Métodos para Calcular el MCM
1. Por Descomposición en Factores Primos
- Descomponer: Realiza la descomposición prima de cada número.
- Identificar: Selecciona todos los factores primos que aparecen (comunes y no comunes).
- Multiplicar: Multiplica esos factores, usando siempre la mayor potencia con la que aparecen en cualquiera de las descomposiciones.
Ejemplo: Calcular el MCM de 12 y 15
- Descomposición de 12: \(2 \times 2 \times 3 = 2^2 \times 3^1\)
- Descomposición de 15: \(3 \times 5 = 3^1 \times 5^1\)
- Factores que aparecen: 2, 3 y 5.
- Mayor exponente del 2: Es 2 (de \(2^2\)).
- Mayor exponente del 3: Es 1 (de \(3^1\)).
- Mayor exponente del 5: Es 1 (de \(5^1\)).
- Cálculo: MCM = \(2^2 \times 3^1 \times 5^1 = 4 \times 3 \times 5 = 60\).
Resultado: MCM(12, 15) = 60.
2. Método de Tabla (Algoritmo Chileno)
- Escribe los números en una fila, separados por una línea vertical.
- Comienza a dividir por el número primo más pequeño (2). Divide los números que sean divisibles y anota el resultado abajo. Si un número no es divisible, simplemente se baja.
- Repite el proceso con el mismo primo hasta que ya no puedas dividir ningún número.
- Pasa al siguiente número primo (3, 5, etc.) y repite el proceso.
- Continúa hasta que todos los números de la fila se hayan reducido a 1.
- El MCM es el producto de todos los números primos que usaste para dividir.
Ejemplo: Calcular el MCM de 12 y 18
\[ \begin{array}{cc|c} 12 & 18 & \mathbf{2} \\ 6 & 9 & \mathbf{2} \\ 3 & 9 & \mathbf{3} \\ 1 & 3 & \mathbf{3} \\ 1 & 1 & \end{array} \]
Multiplicamos los factores de la derecha: \(2 \times 2 \times 3 \times 3 = 36\).
Resultado: MCM(12, 18) = 36.
¡A Practicar!
Ejercicios de Cálculo
Calcula el MCM de los siguientes números:
- 6 y 8
- 10 y 15
- 12, 18 y 24
- 20 y 25
- 14, 21 y 35
- 9, 12 y 15
- 30 y 40
- 24, 36 y 48
- 15, 20, 30 y 45
- 10, 12, 15 y 18
- MCM(6, 8) = 24
- MCM(10, 15) = 30
- MCM(12, 18, 24) = 72
- MCM(20, 25) = 100
- MCM(14, 21, 35) = 210
- MCM(9, 12, 15) = 180
- MCM(30, 40) = 120
- MCM(24, 36, 48) = 144
- MCM(15, 20, 30, 45) = 180
- MCM(10, 12, 15, 18) = 180
Problemas de Aplicación
- Dos trenes salen de una estación a las 8:00 am. Uno sale cada 45 minutos y el otro cada 60 minutos. ¿A qué hora volverán a coincidir en la estación?
- Tres amigos se encuentran en un parque a las 9:00 am. Uno corre cada 12 minutos, otro cada 18 y el tercero cada 24. ¿A qué hora volverán a encontrarse en el punto de partida?
- Dos engranajes de una máquina giran a diferentes velocidades. Uno da una vuelta completa cada 18 segundos y el otro cada 24. ¿Cuántos segundos pasarán hasta que vuelvan a estar en la misma posición inicial?
- Un autobús sale cada 20 minutos y otro cada 30 minutos. Si ambos salen a las 7:00 am, ¿a qué hora volverán a coincidir en la parada?
- Tres luces de colores se encienden juntas a las 10:00 pm. La roja se enciende cada 12 segundos, la verde cada 15 y la azul cada 20. ¿A qué hora volverán a coincidir?
- Dos barcos salen de un puerto a la misma hora. Uno regresa cada 18 días y el otro cada 24. ¿Cuántos días pasarán hasta que ambos barcos vuelvan a estar en el puerto al mismo tiempo?
- Un grupo de amigos se reúne cada 10 días para jugar fútbol, otro grupo se reúne cada 15 días para jugar baloncesto y un tercer grupo se reúne cada 20 días para jugar voleibol. Si los tres grupos se reunieron hoy, ¿cuántos días pasarán hasta que vuelvan a coincidir?
- Cuatro atletas corren en una pista circular. El primero completa una vuelta cada 60 segundos, el segundo cada 75 segundos, el tercero cada 90 segundos y el cuarto cada 100 segundos. Si los cuatro comienzan a correr juntos, ¿cuántos segundos pasarán hasta que vuelvan a coincidir en el punto de partida?
- MCM(45, 60) = 180 minutos (3 horas). Volverán a coincidir a las 11:00 am.
- MCM(12, 18, 24) = 72 minutos. Volverán a encontrarse a las 10:12 am.
- MCM(18, 24) = 72 segundos.
- MCM(20, 30) = 60 minutos. Volverán a coincidir a las 8:00 am.
- MCM(12, 15, 20) = 60 segundos (1 minuto). Volverán a coincidir a las 10:01 pm.
- MCM(18, 24) = 72 días.
- MCM(10, 15, 20) = 60 días.
- MCM(60, 75, 90, 100) = 900 segundos (15 minutos).
3. Usando la Relación entre MCD y MCM
\[ MCM(a, b) = \frac{a \times b}{MCD(a, b)} \]
Ejemplo: Aplicando la fórmula
Problema: Se sabe que el producto de dos números es 360 y su MCD es 6. ¿Cuál es el MCM de esos dos números?
Solución: Usamos la propiedad \( MCM(a, b) = \frac{a \times b}{MCD(a, b)} \).
Reemplazamos los valores conocidos en la fórmula:
\[ MCM = \frac{360}{6} = 60 \]
Por lo tanto, el MCM de esos dos números es 60.
Práctica con la Fórmula MCD y MCM
Usa la propiedad \(MCD(a, b) \times MCM(a, b) = a \times b\) para resolver los siguientes problemas.
- El producto de dos números es 216 y su MCD es 6. ¿Cuál es su MCM?
- El producto de dos números es 1200 y su MCM es 120. ¿Cuál es su MCD?
- Sabiendo que el MCD de 50 y 75 es 25, calcula su MCM usando la fórmula.
- El MCD de dos números es 8 y su MCM es 96. ¿Cuál es el producto de estos dos números?
- Dos números son 12 y 30. Comprueba que el producto de los números es igual al producto de su MCD y su MCM.
- Un número es 15. Sabiendo que el MCD entre este número y otro desconocido es 5, y su MCM es 30, ¿cuál es el otro número?
- Solución: \(MCM = \frac{a \times b}{MCD} = \frac{216}{6} = 36\)
- Solución: \(MCD = \frac{a \times b}{MCM} = \frac{1200}{120} = 10\)
- Solución: \(MCM = \frac{50 \times 75}{25} = \frac{3750}{25} = 150\)
- Solución: \(a \times b = MCD \times MCM = 8 \times 96 = 768\)
- Solución:
- Producto de los números: \(12 \times 30 = 360\)
- MCD(12, 30) = 6
- MCM(12, 30) = 60
- Producto de MCD y MCM: \(6 \times 60 = 360\). ¡Se comprueba la igualdad!
- Solución: \(b = \frac{MCD \times MCM}{a} = \frac{5 \times 30}{15} = \frac{150}{15} = 10\). El otro número es 10.
11. Subconjuntos de los Números Naturales: algunas Sucesiones
Subconjuntos Notables de los Números Naturales
En esta página, exploraremos algunos subconjuntos de los números naturales que forman sucesiones especiales, revelando sus patrones y secretos.
Tipos de Sucesiones Especiales
1. Basadas en la Divisibilidad
Esta distinción surge de la divisibilidad por 2. Los números pares se pueden dividir en dos mitades exactas, mientras que a los impares siempre les "sobra" uno.
- Sucesión de Pares: 2, 4, 6, 8, 10, 12, ... (se suma 2 al anterior).
- Sucesión de Impares: 1, 3, 5, 7, 9, 11, ... (también se suma 2 al anterior).
Los primos son los "bloques de construcción" fundamentales de los números. Son aquellos números mayores que 1 que solo pueden ser divididos de forma exacta por 1 y por sí mismos.
- Sucesión de Primos: 2, 3, 5, 7, 11, 13, 17, ... (su patrón no es una simple suma).
2. Basadas en la Geometría (Números Figurados)
Estos números surgen de la conexión entre aritmética y geometría, al contar los puntos necesarios para formar figuras geométricas.
- Sucesión de Cuadrados: 1, 4, 9, 16, 25, 36, ... (se obtiene elevando al cuadrado: \(1^2, 2^2, 3^2, ...\)).
- Sucesión de Triangulares: 1, 3, 6, 10, 15, 21, ... (se obtiene sumando el siguiente número natural: 1, 1+2, 1+2+3, ...).
3. Basadas en la Naturaleza y Recursión
Esta famosa sucesión surge de un problema sobre la cría de conejos, pero aparece en innumerables patrones de la naturaleza: en los pétalos de las flores, las espirales de las galaxias y las conchas de los caracoles. Cada número de la secuencia es la suma de los dos anteriores.
- Sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, ...
¡Pon a prueba tus conocimientos!
- ¿Cuáles son los primeros 10 números pares?
- ¿Cuál es el décimo número cuadrado?
- Encuentra los primeros 5 números triangulares.
- ¿Es 19 un número primo? ¿Por qué?
- ¿Cuáles son los siguientes tres números en la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, ...?
- Si el quinto número triangular es 15, ¿cuál es el sexto?
- ¿Es 100 un número cuadrado? ¿Por qué?
- Investiga: ¿Qué son los números pentagonales? Escribe los primeros 5.
- Respuesta: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
- Respuesta: 100 (porque \(10^2 = 10 \times 10 = 100\)).
- Respuesta: 1, 3, 6, 10, 15.
- Respuesta: Sí, porque solo es divisible de forma exacta por 1 y 19.
- Respuesta: 13 (5+8), 21 (8+13), y 34 (13+21).
- Respuesta: 21 (se le suma el siguiente número natural: \(15 + 6 = 21\)).
- Respuesta: Sí, porque \(10 \times 10 = 100\).
- Respuesta: Son números figurados que se pueden representar formando pentágonos. Los primeros 5 son: 1, 5, 12, 22, 35.
Existen muchos otros subconjuntos interesantes. ¡Investiga sobre números perfectos, abundantes, deficientes, felices o capicúas! Sigue explorando el fascinante mundo de las matemáticas.
12. Potencias de Números Naturales
Potencias de Números Naturales
Una potencia es una forma abreviada de escribir una multiplicación repetida de un número por sí mismo. Se compone de una base y un exponente.
- Base (2): Es el número que se multiplica.
- Exponente (3): Indica cuántas veces se multiplica la base por sí misma.
- Potencia (8): Es el resultado de la operación.
Se lee "dos elevado a tres" o "dos al cubo", y significa \(2 \times 2 \times 2\).
⚠️ Reglas Especiales que no debes olvidar
- Exponente Cero: Cualquier número (distinto de cero) elevado a la potencia 0 es siempre igual a 1. (Ej: \(7^0 = 1\))
- Exponente Uno: Cualquier número elevado a la potencia 1 es igual al mismo número. (Ej: \(15^1 = 15\))
- Base Uno: El número 1 elevado a cualquier potencia es siempre 1. (Ej: \(1^{10} = 1\))
Ejercicios de Cálculo de Potencias
Calcula el valor de las siguientes potencias:
- \(2^4\)
- \(4^3\)
- \(6^2\)
- \(3^5\)
- \(9^3\)
- \(10^6\)
- \(15^2\)
- \(1^{10}\)
- \(8^0\)
- \(20^2\)
- \(2^4 = 16\)
- \(4^3 = 64\)
- \(6^2 = 36\)
- \(3^5 = 243\)
- \(9^3 = 729\)
- \(10^6 = 1.000.000\)
- \(15^2 = 225\)
- \(1^{10} = 1\)
- \(8^0 = 1\)
- \(20^2 = 400\)
El Árbol de Potencias
El árbol de potencias nos ayuda a ver cómo "crecen" los números al multiplicarlos por sí mismos. Cada nivel del árbol representa un exponente mayor.
Árbol de base 2: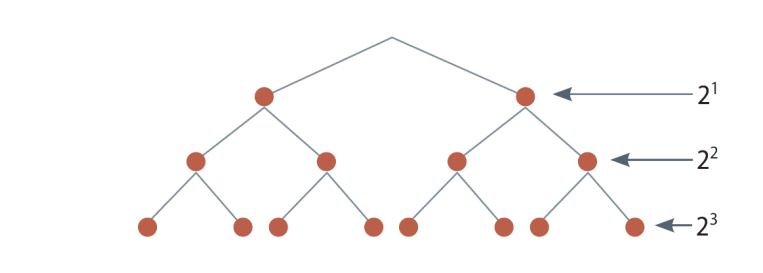
Árbol de base 3: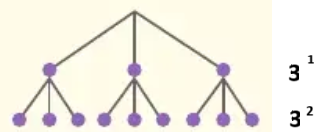
Encontrar la Base
A veces, el desafío es inverso: nos dan el resultado (la potencia) y el exponente, y debemos encontrar la base. Esto es como preguntar: "¿Qué número, multiplicado por sí mismo X veces, da este resultado?"
Ejercicios para Encontrar la Base
Encuentra el valor de \(x\) en cada caso:
- Si \(x^2 = 25\), ¿cuánto vale \(x\)?
- Si \(x^3 = 27\), ¿cuánto vale \(x\)?
- Si \(x^4 = 81\), ¿cuánto vale \(x\)?
- Si \(x^2 = 100\), ¿cuánto vale \(x\)?
- Si \(x^3 = 64\), ¿cuánto vale \(x\)?
- Si \(x^5 = 32\), ¿cuánto vale \(x\)?
- Si \(x^2 = 144\), ¿cuánto vale \(x\)?
- Si \(x^3 = 125\), ¿cuánto vale \(x\)?
- Si \(x^4 = 625\), ¿cuánto vale \(x\)?
- Si \(x^6 = 1\), ¿cuánto vale \(x\)?
- \(x = 5\) (porque \(5 \times 5 = 25\))
- \(x = 3\) (porque \(3 \times 3 \times 3 = 27\))
- \(x = 3\) (porque \(3 \times 3 \times 3 \times 3 = 81\))
- \(x = 10\) (porque \(10 \times 10 = 100\))
- \(x = 4\) (porque \(4 \times 4 \times 4 = 64\))
- \(x = 2\) (porque \(2 \times 2 \times 2 \times 2 \times 2 = 32\))
- \(x = 12\) (porque \(12 \times 12 = 144\))
- \(x = 5\) (porque \(5 \times 5 \times 5 = 125\))
- \(x = 5\) (porque \(5 \times 5 \times 5 \times 5 = 625\))
- \(x = 1\) (porque 1 elevado a cualquier potencia es 1)
Problemas con Potencias
Las potencias no son solo un concepto abstracto, aparecen constantemente en problemas de crecimiento, combinatoria y muchas otras áreas.
- Un edificio tiene 4 pisos. Cada piso tiene 4 departamentos, y en cada departamento viven 4 personas. ¿Cuántas personas viven en el edificio? (Expresa el resultado como una potencia).
- Una bacteria se duplica cada hora. Si al principio hay una bacteria, ¿cuántas habrá después de 5 horas?
- Juan ahorra dinero duplicando la cantidad del día anterior. Si el primer día ahorró $1 (que es \(2^0\)), ¿cuánto dinero habrá ahorrado en total al final del séptimo día?
- En un tablero de ajedrez, se pone 1 grano de trigo en el primer casillero, 2 en el segundo, 4 en el tercero, y así sucesivamente. ¿Cuántos granos hay en el quinto casillero?
- María envía una cadena de mensajes a 3 amigos. Cada amigo la reenvía a otros 3, y estos a su vez a otros 3. ¿Cuántas personas reciben el mensaje en la tercera ronda de reenvíos?
- Solución: \(4 \times 4 \times 4 = 4^3 = 64\) personas.
- Solución: \(2^5 = 32\) bacterias.
- Solución: Se debe sumar lo de cada día: \(2^0 + 2^1 + ... + 2^6\). Esto da \(1+2+4+8+16+32+64 = 127\) pesos. (Una curiosidad: esta suma es siempre \(2^7 - 1\)).
- Solución: El casillero 5 corresponde a la potencia \(2^4 = 16\) granos.
- Solución: \(3 \times 3 \times 3 = 3^3 = 27\) personas.
13. Propiedades de las Potencias
Propiedades de las Potencias
Las potencias tienen varias propiedades que nos permiten simplificar y resolver operaciones de manera más eficiente. A continuación, se presentan las propiedades más importantes, con ejemplos, ejercicios y problemas.
1. Producto de Potencias de Igual Base
\[ a^m \times a^n = a^{m+n} \]
Ejemplo: \(2^3 \times 2^2 = 2^{3+2} = 2^5 = 32\)
Ejercicios
- \(3^2 \times 3^4\)
- \(5^3 \times 5^1\)
- \(10^2 \times 10^5\)
- \(2^6 \times 2^0\)
- \(7^2 \times 7^3 \times 7^1\)
- Si \(2^3 \times 2^x = 2^7\), ¿cuánto vale \(x\)?
- Si \(a^4 \times a^2 = 64\), ¿cuánto vale \(a\)?
- Respuesta: \(3^{2+4} = 3^6 = 729\)
- Respuesta: \(5^{3+1} = 5^4 = 625\)
- Respuesta: \(10^{2+5} = 10^7 = 10.000.000\)
- Respuesta: \(2^{6+0} = 2^6 = 64\)
- Respuesta: \(7^{2+3+1} = 7^6 = 117.649\)
- Respuesta: \(x = 4\)
- Respuesta: \(a^6 = 64 \implies a = 2\)
Problemas
- Un tipo de bacteria duplica su población cada hora. Si inicialmente hay \(2^3\) bacterias, ¿cuántas habrá después de 4 horas? (Expresa la respuesta como una potencia de 2).
- Juan tiene \(3^2\) cajas de canicas. Si en cada caja guarda \(3^3\) canicas, ¿cuántas canicas tiene Juan en total? (Expresa la respuesta como una potencia de 3).
- Si se sabe que \(5^x \times 5^3 = 5^7\), ¿cuántas veces se multiplicó la base 5 por sí misma en total?
- Respuesta: \(2^3 \times 2^4 = 2^7\) bacterias.
- Respuesta: \(3^2 \times 3^3 = 3^5\) canicas.
- Respuesta: 7 veces.
2. Cociente de Potencias de Igual Base
\[ \frac{a^m}{a^n} = a^{m-n} \quad (\text{si } a \neq 0) \]
Ejemplo: \(5^4 \div 5^2 = 5^{4-2} = 5^2 = 25\)
Ejercicios
- \(2^5 \div 2^3\)
- \(7^6 \div 7^2\)
- \(10^8 \div 10^4\)
- \(3^4 \div 3^4\)
- \(6^5 \div 6^1\)
- Si \(3^x \div 3^2 = 3^3\), ¿cuánto vale \(x\)?
- Si \(a^5 \div a^x = a^2\), y se sabe que \(a^5 = 32\), ¿cuánto valen \(a\) y \(x\)?
- Respuesta: \(2^{5-3} = 2^2 = 4\)
- Respuesta: \(7^{6-2} = 7^4 = 2401\)
- Respuesta: \(10^{8-4} = 10^4 = 10.000\)
- Respuesta: \(3^{4-4} = 3^0 = 1\)
- Respuesta: \(6^{5-1} = 6^4 = 1296\)
- Respuesta: \(x = 5\)
- Respuesta: \(a = 2, x = 3\)
Problemas
- Si la población de bacterias se describe con la potencia \(2^6\) y luego de un experimento se reduce a \(2^2\), ¿en qué factor disminuyó la población? (Expresa la respuesta como una potencia de 2).
- Un terreno cuadrado tiene un área de \(10^6\) m². Si se divide en parcelas de \(10^2\) m², ¿cuántas parcelas se obtendrán?
- Si \(7^5 \div 7^x = 7^2\), ¿cuál es el valor de \(x\)?
- Respuesta: Disminuyó en un factor de \(2^6 \div 2^2 = 2^4\).
- Respuesta: \(10^6 \div 10^2 = 10^4\) parcelas.
- Respuesta: \(x = 3\)
3. Potencia de una Potencia
\[ (a^m)^n = a^{m \times n} \]
Ejemplo: \((3^2)^3 = 3^{2 \times 3} = 3^6 = 729\)
Ejercicios
- \((2^3)^2\)
- \((5^2)^4\)
- \((10^1)^5\)
- \((4^3)^0\)
- \((7^2)^3\)
- Si \((2^x)^4 = 2^8\), ¿cuánto vale \(x\)?
- Si \((a^2)^x = 81\) y \(a\) es igual a 3, ¿cuánto vale x?
- Respuesta: \(2^{3 \times 2} = 2^6 = 64\)
- Respuesta: \(5^{2 \times 4} = 5^8 = 390.625\)
- Respuesta: \(10^{1 \times 5} = 10^5 = 100.000\)
- Respuesta: \(4^{3 \times 0} = 4^0 = 1\)
- Respuesta: \(7^{2 \times 3} = 7^6 = 117.649\)
- Respuesta: \(x = 2\)
- Respuesta: \((3^2)^x = 81 \implies 9^x = 81 \implies x = 2\)
Problemas
- Una caja cúbica gigante contiene \(5^3\) cajas medianas. Si apilamos \(5^3\) de estas cajas gigantes para formar un súper cubo, ¿cuántas cajas medianas contendrá en total?
- Un terreno cuadrado tiene un lado que mide \(3^4\) metros. ¿Cuál es su área? (Expresa la respuesta como una potencia de 3).
- Si \((3^x)^4 = 3^{12}\), ¿cuál es el valor de \(x\)?
- Respuesta: \((5^3)^3 = 5^9\) cajas medianas.
- Respuesta: Se puede resolver de dos formas que conectan las propiedades:
- Método 1 (usando Producto de Potencias):
El área es lado × lado, entonces: \(3^4 \times 3^4 = 3^{4+4} = 3^8\) m². - Método 2 (usando Potencia de una Potencia):
El área es lado², entonces: \((3^4)^2 = 3^{4 \times 2} = 3^8\) m².
- Método 1 (usando Producto de Potencias):
- Respuesta: \(x = 3\)
4. Potencias de Exponente 0 y 1
- Exponente 0: Cualquier número (distinto de 0) elevado a 0 es siempre igual a 1.
\[ a^0 = 1 \quad (\text{si } a \neq 0) \] - Exponente 1: Cualquier número elevado a 1 es igual a sí mismo.
\[ a^1 = a \]
Ejemplos: \(8^0 = 1\) y \(6^1 = 6\)
Ejercicios y Problemas
- Resuelve: \(150^0\)
- Resuelve: \( (25 \times 4)^1 \)
- Simplifica la expresión: \( (2^3 \times 5^2)^0 \)
- Si \(x^1 = 19\), ¿cuánto vale x?
- Si \(a^x = 1\) y \(a\) es un número distinto de 1, ¿cuánto vale \(x\)?
- Un objeto tiene una masa de \( (2^5)^1 \) kilogramos. ¿Cuál es su masa?
- Resuelve: \( (100 \div 25)^1 \)
- ¿Cuál es el resultado de la operación \( (7^3 \div 7^3)^0 \)?
- Respuesta: 1
- Respuesta: 100
- Respuesta: 1 (Cualquier base no nula elevada a 0 es 1).
- Respuesta: \(x=19\).
- Respuesta: \(x=0\).
- Respuesta: \(2^5 = 32\) kilogramos.
- Respuesta: \(4^1 = 4\).
- Respuesta: El interior del paréntesis es \(7^0=1\). Luego, \(1^0 = 1\).
5. Potencia de un Producto
\[ (a \times b)^n = a^n \times b^n \]
Ejemplo: \((2 \times 3)^2 = 2^2 \times 3^2 = 4 \times 9 = 36\)
Ejercicios
- \((4 \times 5)^2\)
- \((2 \times 10)^3\)
- \((3 \times 3)^2\)
- \((6 \times 1)^4\)
- \((5 \times 2)^3\)
- Si \((2x)^3 = 1000\), ¿cuánto vale \(x\)?
- Simplifica la expresión: \((4 \times 2)^2 \div 2^4\) y luego resuelve.
- Respuesta: \(4^2 \times 5^2 = 16 \times 25 = 400\)
- Respuesta: \(2^3 \times 10^3 = 8 \times 1000 = 8000\)
- Respuesta: \(3^2 \times 3^2 = 9 \times 9 = 81\) (o \(9^2 = 81\))
- Respuesta: \(6^4 \times 1^4 = 1296 \times 1 = 1296\)
- Respuesta: \(5^3 \times 2^3 = 125 \times 8 = 1000\)
- Respuesta: \(2x = 10 \implies x=5\)
- Respuesta: \((8)^2 \div 16 = 64 \div 16 = 4\)
Problemas
- Un cuadrado grande tiene un lado que mide \(2 \times 5\) cm. ¿Cuál es el área del cuadrado? (Exprésala usando la propiedad).
- Un terreno rectangular mide \(2^3\) metros de largo y \(5^3\) metros de ancho. ¿Cuál es el área del terreno? (Exprésala como la potencia de un producto).
- Si \((2x)^3 = 64\), ¿cuánto vale x?
- Respuesta: Se puede resolver de dos formas:
- Método 1 (calculando primero):
El lado mide \(2 \times 5 = 10\) cm. El área es \(10^2 = 100\) cm². - Método 2 (usando la propiedad):
El área es \( (2 \times 5)^2 \). Aplicando la propiedad, esto es \(2^2 \times 5^2 = 4 \times 25 = 100\) cm².
- Método 1 (calculando primero):
- Respuesta: Área = \(2^3 \times 5^3 = (2 \times 5)^3 = 10^3 = 1000\) m².
- Respuesta: \(2x = 4 \implies x=2\)
6. Potencia de un Cociente
\[ (\frac{a}{b})^n = \frac{a^n}{b^n} \quad (\text{si } b \neq 0) \]
Ejemplo: \((\frac{6}{3})^2 = \frac{6^2}{3^2} = \frac{36}{9} = 4\)
Ejercicios
- \((8 \div 2)^3\)
- \((10 \div 5)^2\)
- \((9 \div 3)^4\)
- \((15 \div 3)^3\)
- \((\frac{1}{2} \div \frac{1}{4})^2\)
- Si \( (x \div 3)^2 = 4 \), ¿cuánto vale \(x\)?
- Si se sabe que \( (12 \div x)^2 = 9 \), ¿cuánto vale \(x\)?
- Respuesta: \(\frac{8^3}{2^3} = \frac{512}{8} = 64\)
- Respuesta: \(\frac{10^2}{5^2} = \frac{100}{25} = 4\)
- Respuesta: \(\frac{9^4}{3^4} = \frac{6561}{81} = 81\)
- Respuesta: \(\frac{15^3}{3^3} = \frac{3375}{27} = 125\)
- Respuesta: \((\frac{1}{2})^2 \div (\frac{1}{4})^2 = \frac{1}{4} \div \frac{1}{16} = 4\)
- Respuesta: \(x=6\)
- Respuesta: \(x=4\)
Problemas
- Si tienes \( (10 \div 2)^2 \) caramelos y quieres repartirlos entre 5 niños, ¿cuántos caramelos le tocan a cada niño?
- Un tanque contiene \( (8 \div 4)^5 \) litros de agua. Si se extrae la mitad, ¿cuántos litros quedan en el tanque? (Expresa la solución usando potencias).
- Si \( (x \div 2)^3=27 \), ¿cuánto vale x?
- Respuesta: Tienes \(5^2 = 25\) caramelos. \(25 \div 5 = 5\) caramelos por niño.
- Respuesta: El tanque tiene \(2^5 = 32\) litros. La mitad es \(32 \div 2 = 16\), que es \(2^4\) litros.
- Respuesta: \(x=6\)
Aquí tienes un resumen de todas las reglas en un solo lugar. ¡Úsalo para repasar!
| Propiedad | Fórmula |
|---|---|
| Producto de Potencias de Igual Base | \(a^m \times a^n = a^{m+n}\) |
| Cociente de Potencias de Igual Base | \(a^m \div a^n = a^{m-n}\) |
| Potencia de una Potencia | \((a^m)^n = a^{m \times n}\) |
| Potencia de un Producto | \((a \times b)^n = a^n \times b^n\) |
| Potencia de un Cociente | \((\frac{a}{b})^n = \frac{a^n}{b^n}\) |
| Exponente Cero | \(a^0 = 1\) |
| Exponente Uno | \(a^1 = a\) |
Práctica Final: Ejercicios Mixtos
En los siguientes ejercicios, las propiedades están mezcladas. Tu desafío es identificar qué regla o combinación de reglas necesitas usar para encontrar la solución. ¡Este es el paso más importante para dominar las potencias!
- Resuelve: \(5^3 \times 5^2\)
- Resuelve: \(10^9 \div 10^7\)
- Resuelve: \((2^4)^3\)
- Resuelve: \(47^0\)
- Resuelve: \((3 \times 5)^2\)
- Encuentra el valor de x: \(3^x \times 3^5 = 3^8\)
- Resuelve: \(7^5 \div 7^5\)
- Encuentra el valor de a: \(a^3 = 64\)
- Resuelve: \((\frac{10}{2})^3\)
- Resuelve: \(19^1\)
- Resuelve: \((b^5)^4\)
- Encuentra el valor de y: \(8^y \div 8^2 = 8^3\)
- Resuelve: \(2^3 \times 2^5 \times 2^1\)
- Resuelve: \( (5^2 \times 3^4)^0 \)
- Si \((a^3)^x = 125\) y \(a\) es 5, ¿cuánto vale x?
- Resuelve: \((2^2 \times 3)^2\)
- Resuelve: \( \frac{5^6}{5^4} \)
- Encuentra el valor de n: \((10^n)^2 = 10^6\)
- Si \((3x)^2 = 81\), ¿cuánto vale x?
- Resuelve: \( (2^5 \div 2^2)^3 \)
- Resuelve: \( \frac{(3^2)^3}{3^4} \)
- Encuentra el valor de b: \(b^2 = 144\)
- Simplifica: \( (x^3 \times x^5) \div x^2 \)
- Resuelve: \( (4^5 \times 4^2)^1 \)
- Resuelve: \( \frac{10^4 \times 10^3}{10^5} \)
- Encuentra el valor de z: \( (z \div 4)^2 = 9 \)
- Simplifica: \( \frac{(a^3 \times b^4)^2}{a^6 \times b^5} \)
- Resuelve: \( \frac{6^5}{2^5 \times 3^5} \)
- Encuentra el valor de x: \( 5^{x-1} = 25 \)
- Un cultivo tiene \(10^2\) bacterias. Si su población se multiplica por \(10^2\) cada hora, ¿cuántas bacterias habrá después de 2 horas?
- Solución: \(5^{3+2} = 5^5 = 3125\)
- Solución: \(10^{9-7} = 10^2 = 100\)
- Solución: \(2^{4 \times 3} = 2^{12} = 4096\)
- Solución: 1
- Solución: \(3^2 \times 5^2 = 9 \times 25 = 225\)
- Solución: \(x+5=8 \implies x=3\)
- Solución: \(7^{5-5} = 7^0 = 1\)
- Solución: \(a=4\) (porque \(4 \times 4 \times 4 = 64\))
- Solución: \((\frac{10}{2})^3 = 5^3 = 125\)
- Solución: 19
- Solución: \(b^{5 \times 4} = b^{20}\)
- Solución: \(y-2=3 \implies y=5\)
- Solución: \(2^{3+5+1} = 2^9 = 512\)
- Solución: 1 (cualquier base no nula elevada a 0 es 1)
- Solución: \((5^3)^x = 125 \implies 125^x = 125 \implies x=1\)
- Solución: \((2^2)^2 \times 3^2 = 2^4 \times 3^2 = 16 \times 9 = 144\)
- Solución: \(5^{6-4} = 5^2 = 25\)
- Solución: \(n \times 2 = 6 \implies n=3\)
- Solución: \(3x = 9 \implies x=3\)
- Solución: \((2^{5-2})^3 = (2^3)^3 = 2^9 = 512\)
- Solución: \(\frac{3^6}{3^4} = 3^2 = 9\)
- Solución: \(b=12\)
- Solución: \(x^8 \div x^2 = x^6\)
- Solución: \(4^{5+2} = 4^7 = 16384\)
- Solución: \(\frac{10^7}{10^5} = 10^2 = 100\)
- Solución: \(z \div 4 = 3 \implies z=12\)
- Solución: \(\frac{a^6 \times b^8}{a^6 \times b^5} = b^{8-5} = b^3\)
- Solución: \(\frac{6^5}{(2 \times 3)^5} = \frac{6^5}{6^5} = 6^0 = 1\)
- Solución: La base 25 se puede escribir como \(5^2\). Entonces \(5^{x-1} = 5^2\), lo que implica que \(x-1=2\), y por lo tanto \(x=3\).
- Solución: Inicial: \(10^2\). Después de 1h: \(10^2 \times 10^2 = 10^4\). Después de 2h: \(10^4 \times 10^2 = 10^6\). Hay \(1.000.000\) de bacterias.