CAPITULO 3 Productos notables
| Sitio: | PROFEARAUCO.CL |
| Curso: | Media 1 |
| Libro: | CAPITULO 3 Productos notables |
| Imprimido por: | Invitado |
| Día: | domingo, 8 de marzo de 2026, 02:57 |
Tabla de contenidos
- 1. Productos Notables
- 2. El Cuadrado de la Suma de Binomios
- 3. Aplicacion cuadrado de binomio
- 4. practica visual 1
- 5. El Cuadrado de la Diferencia de un Binomio
- 6. Multiplicando una Suma por una Diferencia de Binomios
- 7. Practica Integrada
- 8. Aplicando Productos Notables en Diversos Contextos
- 9. Complemento Avanzados: Estrategias Avanzadas con Productos Notables
- 10. Complemento Avanzados: Completando el Cuadrado: ¡Transformando Expresiones!
1. Productos Notables
Descubriendo los Productos Notables: ¡Multiplicar se vuelve más fácil!
Los productos notables son una herramienta muy útil en álgebra que nos permiten simplificar y agilizar la multiplicación de ciertas expresiones. En esta página, vamos a comenzar nuestro viaje explorando la base de todo: la propiedad distributiva.
Repaso de la Propiedad Distributiva
La propiedad distributiva establece que la multiplicación de un número por una suma es igual a la suma de las multiplicaciones de dicho número por cada uno de los sumandos.
- Sumar las frutas de una caja (2 manzanas + 4 naranjas = 6 frutas) y luego multiplicar por el número de cajas (6 frutas/caja × 3 cajas = 18 frutas).
- O bien, calcular cuántas manzanas tienes (3 cajas × 2 manzanas/caja = 6 manzanas) y cuántas naranjas tienes (3 cajas × 4 naranjas/caja = 12 naranjas), y luego sumar ambas cantidades (6 manzanas + 12 naranjas = 18 frutas).
Ambos métodos te dan el mismo resultado. ¡Eso es la propiedad distributiva en acción!
\( a \cdot (b + c) = (a \cdot b) + (a \cdot c) \)
En el ejemplo numérico \(5 \cdot (10 + 4)\), es fácil calcular \(5 \cdot 14 = 70\). Tienes razón. La verdadera magia de la propiedad distributiva aparece en el álgebra.
Si la expresion fuera \(5 \cdot (x + 4)\) no podriamos sumar primero \(x + 4\) porque no son "términos semejantes". ¡Es imposible simplificarlo más! La propiedad distributiva es la única herramienta que nos permite "romper" ese paréntesis en \(5 \cdot (x + 4)\) y seguir trabajando con la expresión. Por eso es fundamental.
Ahora, ¡a practicar con algunos ejercicios!
Ejercicios (Propiedad Distributiva)
✨ Ejemplo Guiado (Nivel 1): Vamos a resolver juntos \( 5 \cdot (10 + 4) \).
Aquí, \(a=5\), \(b=10\) y \(c=4\).
Aplicamos la fórmula \( a \cdot (b + c) = (a \cdot b) + (a \cdot c) \):
\( 5 \cdot (10 + 4) = (5 \cdot 10) + (5 \cdot 4) \)
Calculamos cada multiplicación:
\( = 50 + 20 \)
Y sumamos:
\( = 70 \)
Comprobación: Si sumamos primero dentro del paréntesis, obtenemos \( 5 \cdot (14) \), lo que también es 70. ¡Funciona perfecto!
Nivel 1: Ejercicios simples con números enteros.
Ejercicio 1: \( 3 \cdot (4 + 5) \)
Ejercicio 2: \( 7 \cdot (2 + 8) \)
Ejercicio 3: \( 5 \cdot (9 + 1) \)
Ejercicio 4: \( 2 \cdot (6 + 3) \)
Respuesta 1: \( 3 \cdot (4 + 5) = (3 \cdot 4) + (3 \cdot 5) = 12 + 15 = 27 \)
Respuesta 2: \( 7 \cdot (2 + 8) = (7 \cdot 2) + (7 \cdot 8) = 14 + 56 = 70 \)
Respuesta 3: \( 5 \cdot (9 + 1) = (5 \cdot 9) + (5 \cdot 1) = 45 + 5 = 50 \)
Respuesta 4: \( 2 \cdot (6 + 3) = (2 \cdot 6) + (2 \cdot 3) = 12 + 6 = 18 \)
✨ Ejemplo Guiado (Nivel 2): Resolvamos \( 6 \cdot (\frac{1}{2} + \frac{1}{3}) \).
Distribuimos el 6 a cada fracción dentro del paréntesis:
\( 6 \cdot (\frac{1}{2} + \frac{1}{3}) = (6 \cdot \frac{1}{2}) + (6 \cdot \frac{1}{3}) \)
Ahora, calculamos cada producto. Recuerda que multiplicar un entero por una fracción es multiplicar el entero por el numerador:
\( = \frac{6}{2} + \frac{6}{3} \)
Simplificamos las fracciones:
\( = 3 + 2 = 5 \)
Nivel 2: Ahora con números racionales (decimales y fracciones).
Ejercicio 1: \( 2 \cdot (0.5 + 1.5) \)
Ejercicio 2: \( 4 \cdot (\frac{1}{2} + \frac{3}{4}) \)
Ejercicio 3: \( 3 \cdot (1\frac{1}{2} + 2) \)
Ejercicio 4: \( 0.8 \cdot (5 + 2.5) \)
Respuesta 1: \( 2 \cdot (0.5 + 1.5) = (2 \cdot 0.5) + (2 \cdot 1.5) = 1 + 3 = 4 \)
Respuesta 2: \( 4 \cdot (\frac{1}{2} + \frac{3}{4}) = (4 \cdot \frac{1}{2}) + (4 \cdot \frac{3}{4}) = 2 + 3 = 5 \)
Respuesta 3: \( 3 \cdot (1\frac{1}{2} + 2) = 3 \cdot (\frac{3}{2} + 2) = (3 \cdot \frac{3}{2}) + (3 \cdot 2) = \frac{9}{2} + 6 = 4.5 + 6 = 10.5 \)
Respuesta 4: \( 0.8 \cdot (5 + 2.5) = (0.8 \cdot 5) + (0.8 \cdot 2.5) = 4 + 2 = 6 \)
✨ Ejemplo Guiado (Nivel 3): Expandamos la expresión \( 4x \cdot (2y + 3) \).
Multiplicamos el término de afuera (\(4x\)) por cada término de adentro (\(2y\) y \(3\)).
1. Primer término: \( (4x \cdot 2y) = 8xy \)
2. Segundo término: \( (4x \cdot 3) = 12x \)
Juntamos los resultados:
\( 4x \cdot (2y + 3) = 8xy + 12x \)
Nivel 3: Mezclando números y letras (álgebra).
1. \( 2 \cdot (3 + 4) \)
2. \( 5 \cdot (1.2 + 2.8) \)
3. \( \frac{1}{3} \cdot (6 + 9) \)
4. \( 2\frac{1}{4} \cdot (4 + 8) \)
5. \( 3 \cdot (x + 4) \)
6. \( a \cdot (2 + 7) \)
7. \( 0.5 \cdot (4a + 6) \)
8. \( \frac{2}{3} \cdot (6x + 9y) \)
9. \( 4 \cdot (2a + 3b) \)
10. \( x \cdot (y + z) \)
11. \( 1.2 \cdot (5m + 2.5n) \)
12. \( 2 \cdot (x + y + 3) \)
13. \( m \cdot (2 + n + p) \)
14. \( \frac{1}{2} \cdot (4x + 6y + 8z) \)
R1: \( 14 \)
R2: \( 20 \)
R3: \( 5 \)
R4: \( 27 \)
R5: \( 3x + 12 \)
R6: \( 9a \)
R7: \( 2a + 3 \)
R8: \( 4x + 6y \)
R9: \( 8a + 12b \)
R10: \( xy + xz \)
R11: \( 6m + 3n \)
R12: \( 2x + 2y + 6 \)
R13: \( 2m + mn + mp \)
R14: \( 2x + 3y + 4z \)
Yendo al revés: La Factorización
Por ejemplo: en \(3x + 12\), nos preguntamos: ¿qué número o letra se repite en ambos términos? Vemos que 12 es \(3 \cdot 4\), entonces el 3 es un factor común. Así, \(3x + 12 = 3(x + 4)\).
✨ Ejemplo Guiado (Nivel 4): Vamos a factorizar la expresión \( 12a^2b + 18ab^2 \).
Buscamos el Máximo Factor Común (MFC) pieza por pieza:
- Números (12 y 18): El número más grande que divide a ambos es el 6.
- Letra 'a' (\(a^2\) y \(a\)): Escogemos la de menor exponente, es decir, a.
- Letra 'b' (\(b\) y \(b^2\)): Escogemos la de menor exponente, es decir, b.
Nuestro MFC es \(6ab\). Ahora, lo ponemos fuera de un paréntesis y dividimos cada término original por él:
\( \frac{12a^2b}{6ab} = 2a \)
\( \frac{18ab^2}{6ab} = 3b \)
El resultado final es:
\( 12a^2b + 18ab^2 = 6ab(2a + 3b) \)
Nivel 4: Factoriza las siguientes expresiones algebraicas.
1. \( 6x + 9y \)
2. \( 10ab + 15ac \)
3. \( 4m + 12mn \)
4. \( 7xy + 14xz \)
5. \( 2a + 4b + 8c \)
6. \( 5x + 10x^2 \)
7. \( 18abc + 9ad \)
8. \( \frac{1}{2}x + \frac{3}{2}y \)
9. \( 2.5m + 5n \)
10. \( 3ab + 6ac + 9ad \)
11. \( 14x + 7y \)
12. \( 8mn + 4m \)
13. \( \frac{3}{4}a + \frac{1}{4}b \)
14. \( 9x + 6xy + 3xz \)
R1: \( 3(2x + 3y) \)
R2: \( 5a(2b + 3c) \)
R3: \( 4m(1 + 3n) \)
R4: \( 7x(y + 2z) \)
R5: \( 2(a + 2b + 4c) \)
R6: \( 5x(1 + 2x) \)
R7: \( 9a(2bc + d) \)
R8: \( \frac{1}{2}(x + 3y) \)
R9: \( 2.5(m + 2n) \)
R10: \( 3a(b + 2c + 3d) \)
R11: \( 7(2x + y) \)
R12: \( 4m(2n + 1) \)
R13: \( \frac{1}{4}(3a + b) \)
R14: \( 3x(3 + 2y + z) \)
Aplicaciones: Problemas de la vida real
✨ Ejemplo Guiado: Calculando una compra
Problema: Imagina que para una convivencia compras 4 bebidas a $1.200 cada una y 4 paquetes de galletas a $800 cada uno. ¿Cuánto gastas en total?
Podemos resolver esto de dos formas que demuestran la propiedad distributiva:
Método 1: Sumar los costos individuales.
Calculamos el total de las bebidas y el total de las galletas por separado y luego sumamos.
\( (4 \cdot 1200) + (4 \cdot 800) = 4800 + 3200 = \$8000 \)
Método 2: Usar la distributividad (factorizando).
Como compramos 4 unidades de cada cosa, podemos sumar el precio de "un combo" (bebida + galletas) y luego multiplicar por 4.
\( 4 \cdot (1200 + 800) = 4 \cdot (2000) = \$8000 \)
Conclusión: Ambos caminos llevan al mismo resultado. La propiedad distributiva nos permite pasar de una forma a la otra.
Problema 1: Tres amigos van a un complejo deportivo. Cada uno debe pagar una entrada de $5.000 y arrendar un casillero por $1.500. ¿Cuál es el costo total para el grupo? (Exprésalo usando la propiedad distributiva).
Respuesta: El costo por persona es \( (5000 + 1500) \). Como son 3 personas, el total es:
\( 3 \cdot (5000 + 1500) = (3 \cdot 5000) + (3 \cdot 1500) = 15000 + 4500 = \$19.500 \)
Problema 2: Un terreno rectangular se divide en dos para plantar. La primera sección tiene un largo de 10 metros y la segunda tiene un largo de 8 metros. Ambas secciones tienen el mismo ancho de \(x\) metros. Escribe una expresión simplificada para el área total del terreno.
Respuesta: El área total es el ancho por la suma de los largos: \( x \cdot (10 + 8) \).
Aplicando la propiedad distributiva: \( (x \cdot 10) + (x \cdot 8) = 10x + 8x = 18x \).
El área total es de \(18x\) metros cuadrados.
Problema 3: Una tienda de ropa tiene una oferta de "20% de descuento en el total de tu compra". Ana elige una polera de $12.000 y un pantalón de $25.000. ¿Cuánto pagará Ana en total?
(Pista: Pagar con un 20% de descuento es lo mismo que pagar el 80% del precio original).
Respuesta: El costo total sin descuento es \( (12000 + 25000) \). Se debe pagar el 80% (o 0.8) de ese total.
Total a pagar = \( 0.8 \cdot (12000 + 25000) \)
Total a pagar = \( 0.8 \cdot (37000) = \$29.600 \)
El Gran Salto: De la Distribución al Primer Producto Notable
Has dominado la propiedad distributiva. ¿Qué pasa si te pido calcular \( (x+3)^2 \)?
Recuerda que elevar al cuadrado es multiplicar por sí mismo: \( (x+3)^2 = (x+3)(x+3) \). Para resolverlo, distribuiremos cada parte del primer paréntesis sobre el segundo. ¡Vamos a usar colores para que quede más claro!
\( (\textcolor{blue}{x} \textcolor{red}{+3})(x+3) \)
Paso 1: Tomamos la primera parte (\(\textcolor{blue}{x}\)) y la multiplicamos por todo el segundo paréntesis.
\( \textcolor{blue}{x}(x+3) = (\textcolor{blue}{x} \cdot x) + (\textcolor{blue}{x} \cdot 3) = \textcolor{blue}{x^2 + 3x} \)
Paso 2: Ahora tomamos la segunda parte (\(\textcolor{red}{+3}\)) y hacemos exactamente lo mismo.
\( \textcolor{red}{+3}(x+3) = (\textcolor{red}{+3} \cdot x) + (\textcolor{red}{+3} \cdot 3) = \textcolor{red}{+3x + 9} \)
Paso 3: Finalmente, juntamos todos los resultados y sumamos los "términos semejantes".
\( \textcolor{blue}{x^2 + 3x} \textcolor{red}{+3x + 9} = x^2 + 6x + 9 \)
¡Así, hemos demostrado que \( (x+3)^2 = x^2 + 6x + 9 \) !
El patrón general para el Cuadrado de un Binomio es:
\( (a+b)^2 = a^2 + 2ab + b^2 \)
Que se lee: "El primer término al cuadrado, más el doble del primero por el segundo, más el segundo al cuadrado". ¡Esto es lo que exploraremos en la siguiente lección!
2. El Cuadrado de la Suma de Binomios
El Cuadrado de un Binomio: El Caso de la Suma
Ahora que hemos repasado la propiedad distributiva, estamos listos para explorar uno de los productos notables más importantes: el cuadrado de un binomio. En esta página, nos enfocaremos en el caso de la suma, es decir, expresiones de la forma \((a + b)^2\).
Desarrollo del Producto Notable (a + b)²
Elevar un binomio al cuadrado significa multiplicarlo por sí mismo. Entonces, \((a + b)^2\) es lo mismo que \((a + b) \cdot (a + b)\). Usando la propiedad distributiva que ya conocemos, podemos ver el desarrollo:
\( (a + b)^2 = (a + b) \cdot (a + b) \)
\( = a \cdot (a + b) + b \cdot (a + b) \)
\( = a^2 + ab + ba + b^2 \)
\( = a^2 + 2ab + b^2 \)
El desarrollo de un cuadrado de binomio siempre sigue este patrón:
\( (a + b)^2 = a^2 + 2ab + b^2 \)
Se puede leer como: "el primer término al cuadrado, más el doble del producto del primer por el segundo término, más el segundo término al cuadrado".
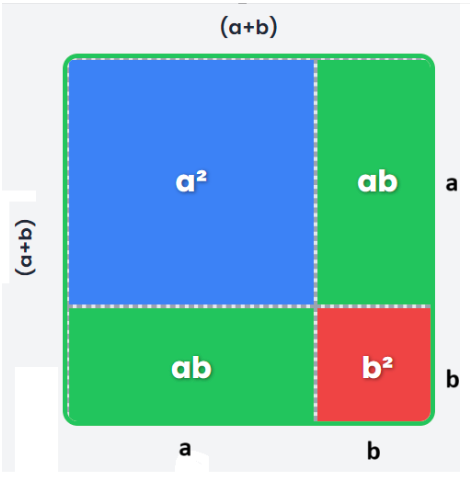
Ejercicios (Cuadrado de un Binomio - Suma)
✨ Ejemplo Guiado (Nivel 1): Resolvamos \( (4 + 2)^2 \) usando la fórmula.
Aplicamos la fórmula \( (a+b)^2 = a^2 + 2ab + b^2 \), donde \(a=4\) y \(b=2\).
Desarrollo: \( (4)^2 + 2 \cdot 4 \cdot 2 + (2)^2 \)
\( = 16 + 16 + 4 \)
\( = 36 \)
Comprobación: \( (4 + 2)^2 = (6)^2 = 36 \). ¡El resultado es el mismo!
Nivel 1: Expandir con valores enteros.
Ejercicio 1: \( (2 + 3)^2 \)
Ejercicio 2: \( (5 + 1)^2 \)
Ejercicio 3: \( (4 + 6)^2 \)
Ejercicio 4: \( (7 + 2)^2 \)
R1: \( (2 + 3)^2 = 2^2 + 2 \cdot 2 \cdot 3 + 3^2 = 4 + 12 + 9 = 25 \)
R2: \( (5 + 1)^2 = 5^2 + 2 \cdot 5 \cdot 1 + 1^2 = 25 + 10 + 1 = 36 \)
R3: \( (4 + 6)^2 = 4^2 + 2 \cdot 4 \cdot 6 + 6^2 = 16 + 48 + 36 = 100 \)
R4: \( (7 + 2)^2 = 7^2 + 2 \cdot 7 \cdot 2 + 2^2 = 49 + 28 + 4 = 81 \)
✨ Ejemplo Guiado (Nivel 2): Resolvamos \( (1.5 + 0.5)^2 \) usando la fórmula.
Aplicamos la fórmula, donde \(a=1.5\) y \(b=0.5\).
Desarrollo: \( (1.5)^2 + 2 \cdot (1.5) \cdot (0.5) + (0.5)^2 \)
\( = 2.25 + 1.5 + 0.25 \)
\( = 4 \)
Comprobación: \( (1.5 + 0.5)^2 = (2)^2 = 4 \). ¡Nuevamente funciona!
Nivel 2: Expandir con valores racionales.
Ejercicio 1: \( (0.5 + 1)^2 \)
Ejercicio 2: \( (\frac{1}{2} + \frac{1}{4})^2 \)
Ejercicio 3: \( (2 + 1\frac{1}{2})^2 \)
Ejercicio 4: \( (1.2 + 0.8)^2 \)
R1: \( (0.5 + 1)^2 = 0.5^2 + 2 \cdot 0.5 \cdot 1 + 1^2 = 0.25 + 1 + 1 = 2.25 \)
R2: \( (\frac{1}{2} + \frac{1}{4})^2 = (\frac{1}{2})^2 + 2 \cdot \frac{1}{2} \cdot \frac{1}{4} + (\frac{1}{4})^2 = \frac{1}{4} + \frac{1}{4} + \frac{1}{16} = \frac{9}{16} \)
R3: \( (2 + 1\frac{1}{2})^2 = (2 + \frac{3}{2})^2 = 2^2 + 2 \cdot 2 \cdot \frac{3}{2} + (\frac{3}{2})^2 = 4 + 6 + \frac{9}{4} = 12.25 \)
R4: \( (1.2 + 0.8)^2 = 1.2^2 + 2 \cdot 1.2 \cdot 0.8 + 0.8^2 = 1.44 + 1.92 + 0.64 = 4 \)
✨ Ejemplo Guiado (Nivel 3): Expandamos \( (3x + 2y)^2 \).
¡Ojo aquí! El primer término es \(a=3x\) y el segundo es \(b=2y\).
1. Primer término al cuadrado: \( (3x)^2 = 3^2 \cdot x^2 = 9x^2 \)
2. El doble del primero por el segundo: \( 2 \cdot (3x) \cdot (2y) = 12xy \)
3. Segundo término al cuadrado: \( (2y)^2 = 2^2 \cdot y^2 = 4y^2 \)
Resultado: \( 9x^2 + 12xy + 4y^2 \)
Nivel 3: Expandir con expresiones algebraicas.
1. \( (x + 2)^2 \)
2. \( (3 + a)^2 \)
3. \( (m + n)^2 \)
4. \( (2x + 1)^2 \)
5. \( (4 + 3y)^2 \)
6. \( (\frac{1}{2}a + 2)^2 \)
7. \( (0.5x + 1.5)^2 \)
8. \( (x + y)^2 \)
9. \( (2a + 3b)^2 \)
10. \( (m + \frac{1}{3})^2 \)
11. \( (2.5 + x)^2 \)
12. \( (3x + 4y)^2 \)
13. \( (\frac{2}{5}m + \frac{3}{5}n)^2 \)
14. \( (1 + 0.1x)^2 \)
R1: \( x^2 + 4x + 4 \)
R2: \( 9 + 6a + a^2 \)
R3: \( m^2 + 2mn + n^2 \)
R4: \( 4x^2 + 4x + 1 \)
R5: \( 16 + 24y + 9y^2 \)
R6: \( \frac{1}{4}a^2 + 2a + 4 \)
R7: \( 0.25x^2 + 1.5x + 2.25 \)
R8: \( x^2 + 2xy + y^2 \)
R9: \( 4a^2 + 12ab + 9b^2 \)
R10: \( m^2 + \frac{2}{3}m + \frac{1}{9} \)
R11: \( 6.25 + 5x + x^2 \)
R12: \( 9x^2 + 24xy + 16y^2 \)
R13: \( \frac{4}{25}m^2 + \frac{12}{25}mn + \frac{9}{25}n^2 \)
R14: \( 1 + 0.2x + 0.01x^2 \)
- Incorrecto: \( 2x^2 \)...
- Correcto: \( (2x)^2 = 4x^2 \)
Factorizando un Trinomio Cuadrado Perfecto
Ahora, haremos el proceso inverso. Si tenemos una expresión como \(a^2 + 2ab + b^2\), podemos "contraerla" a su forma original \((a+b)^2\). A esto se le llama factorizar.
Para factorizar \(x^2 + 6x + 9\), seguimos estos pasos:
- Identificar las raíces de los extremos: La raíz cuadrada de \(x^2\) es \(x\). La raíz cuadrada de \(9\) es \(3\).
- Verificar el término del medio: Multiplicamos las raíces que encontramos y luego por 2. ¿Coincide con el término del medio?
\(2 \cdot x \cdot 3 = 6x\). ¡Sí, coincide! - Escribir el resultado: Como se cumplen las condiciones, la factorización es el binomio formado por las raíces, al cuadrado.
\(x^2 + 6x + 9 = (x + 3)^2\)
✨ Ejemplo Guiado (Nivel 4): Factoricemos \( 4x^2 + 20x + 25 \).
Paso 1: ¿Tienen raíz cuadrada exacta los extremos?
- La raíz de \(4x^2\) es \(2x\).
- La raíz de \(25\) es \(5\).
Paso 2: ¿El término del medio es el doble producto de esas raíces?
Verificamos: \( 2 \cdot (2x) \cdot (5) = 20x \). ¡Sí, coincide!
Paso 3: Escribimos el resultado.
Como todo calza, la factorización es \( (2x + 5)^2 \).
Nivel 4: Factoriza los siguientes trinomios cuadrados perfectos.
1. \( x^2 + 4x + 4 \)
2. \( a^2 + 6a + 9 \)
3. \( m^2 + 10m + 25 \)
4. \( 4x^2 + 4x + 1 \)
5. \( 9y^2 + 24y + 16 \)
6. \( \frac{1}{4}a^2 + 2a + 4 \)
7. \( 0.25x^2 + 1.5x + 2.25 \)
8. \( x^2 + 2xy + y^2 \)
9. \( 4a^2 + 12ab + 9b^2 \)
10. \( m^2 + \frac{2}{3}m + \frac{1}{9} \)
11. \( 6.25 + 5x + x^2 \)
12. \( 9x^2 + 24xy + 16y^2 \)
13. \( \frac{4}{25}m^2 + \frac{12}{25}mn + \frac{9}{25}n^2 \)
14. \( 1 + 0.2x + 0.01x^2 \)
R1: \( (x + 2)^2 \)
R2: \( (a + 3)^2 \)
R3: \( (m + 5)^2 \)
R4: \( (2x + 1)^2 \)
R5: \( (3y + 4)^2 \)
R6: \( (\frac{1}{2}a + 2)^2 \)
R7: \( (0.5x + 1.5)^2 \)
R8: \( (x + y)^2 \)
R9: \( (2a + 3b)^2 \)
R10: \( (m + \frac{1}{3})^2 \)
R11: \( (2.5 + x)^2 \)
R12: \( (3x + 4y)^2 \)
R13: \( (\frac{2}{5}m + \frac{3}{5}n)^2 \)
R14: \( (1 + 0.1x)^2 \)
Problemas de Aplicación
✨ Ejemplo Guiado: Calculando un perímetro a partir del área
Problema: Una pequeña plaza cuadrada tiene un área de \(x^2 + 10x + 25\) metros cuadrados. Si un jardinero quiere poner una cinta decorativa por todo el borde, ¿cuántos metros de cinta necesita?
Paso 1: Entender el problema.
Nos dan el área y nos piden el perímetro (la longitud de la cinta). Sabemos que para un cuadrado:
- Área = \(lado^2\)
- Perímetro = \(4 \cdot lado\)
Para encontrar el perímetro, primero necesitamos conocer la medida del lado.
Paso 2: Encontrar el lado a partir del área.
Si el Área = \( (x^2 + 10x + 25) \), entonces el lado es la raíz cuadrada de esa expresión. ¡Para eso factorizamos el trinomio!
- La raíz de \(x^2\) es \(x\).
- La raíz de \(25\) es \(5\).
- Verificamos el término del medio: \(2 \cdot x \cdot 5 = 10x\). ¡Coincide!
Entonces, la factorización es \( (x+5)^2 \). Esto significa que el lado de la plaza mide \( (x+5) \) metros.
Paso 3: Calcular el perímetro.
Ahora multiplicamos el lado por 4:
Perímetro = \(4 \cdot (x+5)\)
Perímetro = \(4x + 20\)
Respuesta Final: El jardinero necesita \( (4x + 20) \) metros de cinta.
Problema 1: El área de un cuadrado es \(x^2 + 6x + 9\) unidades cuadradas. ¿Cuál es la longitud del lado del cuadrado en términos de \(x\)?
Respuesta: Factorizando la expresión \(x^2 + 6x + 9\), obtenemos \((x + 3)^2\). Por lo tanto, la longitud del lado del cuadrado es \( (x + 3) \) unidades.
Problema 2: Se quiere construir una piscina cuadrada rodeada por un borde de baldosas. El área total (piscina más borde) se puede expresar como \(4x^2 + 28x + 49\) metros cuadrados. ¿Cuál es la expresión que representa la longitud del lado del área total?
Respuesta: Factorizando la expresión \(4x^2 + 28x + 49\), obtenemos \((2x + 7)^2\). Esto representa el área total. Por lo tanto, la longitud del lado del área total (piscina más el borde) es \( (2x + 7) \) metros.
Problema 3: Un terreno cuadrado tiene un área de \(9x^2 + 30xy + 25y^2\) metros cuadrados. Si se quiere cercar el terreno con una valla, ¿cuántos metros de valla se necesitan?
Respuesta: Factorizando la expresión \(9x^2 + 30xy + 25y^2\), obtenemos \((3x + 5y)^2\). Esto significa que la longitud de un lado del terreno es \( (3x + 5y) \) metros. El perímetro de un cuadrado es 4 veces su lado, por lo tanto, se necesitan \(4 \cdot (3x + 5y) = 12x + 20y\) metros de valla.
3. Aplicacion cuadrado de binomio
Interactúa con la siguiente aplicación para comprender el cuadrado de un binomio.
4. practica visual 1
Interactúa con la siguiente aplicación para comprender el cuadrado de un binomio.
5. El Cuadrado de la Diferencia de un Binomio
El Cuadrado de un Binomio: El Caso de la Resta
En la página anterior, exploramos el cuadrado de un binomio cuando se trata de una suma \((a + b)^2\). Ahora, vamos a analizar el caso de la resta, es decir, expresiones de la forma \((a - b)^2\).
Desarrollo del Producto Notable (a - b)²
Al igual que con la suma, elevar un binomio al cuadrado significa multiplicarlo por sí mismo. Entonces, \((a - b)^2\) es lo mismo que \((a - b) \cdot (a - b)\). Usando la propiedad distributiva, desarrollamos esta expresión:
\( (a - b)^2 = (a - b) \cdot (a - b) \)
\( = a \cdot (a - b) - b \cdot (a - b) \)
\( = (a \cdot a) - (a \cdot b) - (b \cdot a) + (b \cdot b) \)
\( = a^2 - ab - ba + b^2 \)
\( = a^2 - 2ab + b^2 \)
El desarrollo siempre sigue este patrón, ¡fíjate bien en los signos!
\( (a - b)^2 = a^2 - 2ab + b^2 \)
Se puede leer como: "el primer término al cuadrado, menos el doble del producto del primer por el segundo término, más el segundo término al cuadrado".
Ejercicios (Cuadrado de un Binomio - Resta)
✨ Ejemplo Guiado (Nivel 1): Resolvamos \( (7 - 3)^2 \) usando la fórmula.
Aplicamos la fórmula \( (a-b)^2 = a^2 - 2ab + b^2 \), donde \(a=7\) y \(b=3\).
Desarrollo: \( (7)^2 - 2 \cdot 7 \cdot 3 + (3)^2 \)
\( = 49 - 42 + 9 \)
\( = 16 \)
Comprobación: \( (7 - 3)^2 = (4)^2 = 16 \). ¡El resultado es el mismo!
Nivel 1: Expandir con valores enteros.
Ejercicio 1: \( (5 - 2)^2 \)
Ejercicio 2: \( (8 - 3)^2 \)
Ejercicio 3: \( (4 - 1)^2 \)
Ejercicio 4: \( (9 - 5)^2 \)
R1: \( (5 - 2)^2 = 5^2 - 2 \cdot 5 \cdot 2 + 2^2 = 25 - 20 + 4 = 9 \)
R2: \( (8 - 3)^2 = 8^2 - 2 \cdot 8 \cdot 3 + 3^2 = 64 - 48 + 9 = 25 \)
R3: \( (4 - 1)^2 = 4^2 - 2 \cdot 4 \cdot 1 + 1^2 = 16 - 8 + 1 = 9 \)
R4: \( (9 - 5)^2 = 9^2 - 2 \cdot 9 \cdot 5 + 5^2 = 81 - 90 + 25 = 16 \)
✨ Ejemplo Guiado (Nivel 2): Resolvamos \( (2.5 - 1)^2 \) usando la fórmula.
Aplicamos la fórmula, donde \(a=2.5\) y \(b=1\).
Desarrollo: \( (2.5)^2 - 2 \cdot (2.5) \cdot (1) + (1)^2 \)
\( = 6.25 - 5 + 1 \)
\( = 2.25 \)
Comprobación: \( (2.5 - 1)^2 = (1.5)^2 = 2.25 \). ¡Perfecto!
Nivel 2: Expandir con valores racionales.
Ejercicio 1: \( (1 - 0.5)^2 \)
Ejercicio 2: \( (\frac{3}{4} - \frac{1}{2})^2 \)
Ejercicio 3: \( (3 - 1\frac{1}{2})^2 \)
Ejercicio 4: \( (2.5 - 0.5)^2 \)
R1: \( (1 - 0.5)^2 = 1^2 - 2 \cdot 1 \cdot 0.5 + 0.5^2 = 1 - 1 + 0.25 = 0.25 \)
R2: \( (\frac{3}{4} - \frac{1}{2})^2 = (\frac{3}{4})^2 - 2 \cdot \frac{3}{4} \cdot \frac{1}{2} + (\frac{1}{2})^2 = \frac{9}{16} - \frac{3}{4} + \frac{1}{4} = \frac{1}{16} \)
R3: \( (3 - 1\frac{1}{2})^2 = (3 - \frac{3}{2})^2 = 3^2 - 2 \cdot 3 \cdot \frac{3}{2} + (\frac{3}{2})^2 = 9 - 9 + \frac{9}{4} = 2.25 \)
R4: \( (2.5 - 0.5)^2 = 2.5^2 - 2 \cdot 2.5 \cdot 0.5 + 0.5^2 = 6.25 - 2.5 + 0.25 = 4 \)
✨ Ejemplo Guiado (Nivel 3): Expandamos \( (4x - y)^2 \).
Aquí, el primer término es \(a=4x\) y el segundo es \(b=y\).
1. Primer término al cuadrado: \( (4x)^2 = 16x^2 \)
2. Menos el doble del primero por el segundo: \( -2 \cdot (4x) \cdot (y) = -8xy \)
3. Más el segundo término al cuadrado: \( (y)^2 = y^2 \)
Resultado: \( 16x^2 - 8xy + y^2 \)
Nivel 3: Expandir con expresiones algebraicas.
1. \( (x - 3)^2 \)
2. \( (a - 5)^2 \)
3. \( (m - n)^2 \)
4. \( (3x - 2)^2 \)
5. \( (5 - 2y)^2 \)
6. \( (2a - \frac{1}{2})^2 \)
7. \( (1.5 - 0.5x)^2 \)
8. \( (x - y)^2 \)
9. \( (4a - 3b)^2 \)
10. \( (\frac{2}{3} - m)^2 \)
11. \( (x - 2.5)^2 \)
12. \( (5x - 2y)^2 \)
13. \( (\frac{1}{2}m - \frac{2}{3}n)^2 \)
14. \( (0.2x - 1)^2 \)
R1: \( x^2 - 6x + 9 \)
R2: \( a^2 - 10a + 25 \)
R3: \( m^2 - 2mn + n^2 \)
R4: \( 9x^2 - 12x + 4 \)
R5: \( 25 - 20y + 4y^2 \)
R6: \( 4a^2 - 2a + \frac{1}{4} \)
R7: \( 2.25 - 1.5x + 0.25x^2 \)
R8: \( x^2 - 2xy + y^2 \)
R9: \( 16a^2 - 24ab + 9b^2 \)
R10: \( \frac{4}{9} - \frac{4}{3}m + m^2 \)
R11: \( x^2 - 5x + 6.25 \)
R12: \( 25x^2 - 20xy + 4y^2 \)
R13: \( \frac{1}{4}m^2 - \frac{2}{3}mn + \frac{4}{9}n^2 \)
R14: \( 0.04x^2 - 0.4x + 1 \)
- El término del medio en la fórmula, \(2ab\), está precedido por un signo negativo.
- El último término, \(b^2\), siempre es POSITIVO. Esto se debe a que al desarrollar la multiplicación, el término proviene de \((-b) \cdot (-b)\), y la regla de los signos nos dice que 'menos por menos es más'.
Factorizando un Trinomio Cuadrado Perfecto (con Resta)
Para factorizar una expresión de la forma \(a^2 - 2ab + b^2\), buscamos el binomio \((a-b)^2\) que la originó.
✨ Ejemplo Guiado (Nivel 4): Factoricemos \( 9x^2 - 12x + 4 \).
Paso 1: ¿Tienen raíz cuadrada exacta los extremos?
- La raíz de \(9x^2\) es \(3x\).
- La raíz de \(4\) es \(2\).
Paso 2: ¿El término del medio es el doble producto (negativo) de esas raíces?
Verificamos: \( -2 \cdot (3x) \cdot (2) = -12x \). ¡Sí, coincide!
Paso 3: Escribimos el resultado.
Como el término del medio es negativo, la factorización es una resta: \( (3x - 2)^2 \).
Nivel 4: Factorizar los siguientes trinomios.
1. \( x^2 - 6x + 9 \)
2. \( a^2 - 10a + 25 \)
3. \( m^2 - 4m + 4 \)
4. \( 9x^2 - 6x + 1 \)
5. \( 4y^2 - 12y + 9 \)
6. \( a^2 - a + \frac{1}{4} \)
7. \( 4x^2 - 4x + 1 \)
8. \( x^2 - 2xy + y^2 \)
9. \( 16a^2 - 40ab + 25b^2 \)
10. \( m^2 - \frac{4}{3}m + \frac{4}{9} \)
11. \( x^2 - 5x + 6.25 \)
12. \( 4x^2 - 12xy + 9y^2 \)
13. \( \frac{9}{4}m^2 - 3mn + n^2 \)
14. \( 0.04x^2 - 0.4x + 1 \)
R1: \( (x - 3)^2 \)
R2: \( (a - 5)^2 \)
R3: \( (m - 2)^2 \)
R4: \( (3x - 1)^2 \)
R5: \( (2y - 3)^2 \)
R6: \( (a - \frac{1}{2})^2 \)
R7: \( (2x - 1)^2 \)
R8: \( (x - y)^2 \)
R9: \( (4a - 5b)^2 \)
R10: \( (m - \frac{2}{3})^2 \)
R11: \( (x - 2.5)^2 \)
R12: \( (2x - 3y)^2 \)
R13: \( (\frac{3}{2}m - n)^2 \)
R14: \( (0.2x - 1)^2 \)
Problemas de Aplicación
✨ Ejemplo Guiado (Nivel 5): Un artista tiene un lienzo cuadrado cuya área se representa por la expresión \(x^2 - 18x + 81\) cm². ¿Cuál es la longitud del lado del lienzo?
Paso 1: Entender el problema.
Nos dan el área de un cuadrado y nos piden la medida de su lado. Sabemos que Área = \(lado^2\), por lo tanto, el lado es la raíz cuadrada del área.
Paso 2: Encontrar el lado factorizando.
Debemos factorizar el trinomio \(x^2 - 18x + 81\).
- La raíz de \(x^2\) es \(x\).
- La raíz de \(81\) es \(9\).
- Verificamos el término del medio: \( -2 \cdot x \cdot 9 = -18x \). ¡Coincide!
Respuesta: Como la factorización es \( (x - 9)^2 \), la longitud del lado del lienzo es \( (x - 9) \) cm.
Problema 1: El área de un cuadrado es \(x^2 - 14x + 49\) unidades cuadradas. ¿Cuál es la longitud del lado del cuadrado en términos de \(x\)?
Respuesta: Factorizando la expresión \(x^2 - 14x + 49\), obtenemos \((x - 7)^2\). Por lo tanto, la longitud del lado del cuadrado es \( (x - 7) \) unidades.
Problema 2: Un escenario cuadrado tiene un área de \(9x^2 - 12x + 4\) metros cuadrados. Se quiere colocar una alfombra que cubra todo el escenario. ¿Cuáles son las dimensiones de la alfombra en términos de \(x\)?
Respuesta: Factorizando la expresión \(9x^2 - 12x + 4\), obtenemos \((3x - 2)^2\). Como el escenario es cuadrado, la alfombra también debe ser cuadrada. Por lo tanto, las dimensiones de la alfombra son \((3x - 2)\) metros por \((3x - 2)\) metros.
Problema 3: Se tiene un terreno cuadrado de lado "a" metros. Dentro de él se construye una piscina cuadrada de lado "b" metros. El área restante, que corresponde al pasto, se puede expresar como \(a^2 - 6ab + 9b^2\). ¿Cuál es la relación entre el lado del terreno y el lado de la piscina?
Respuesta: El problema está mal planteado. El área restante debería ser a² - b². La expresión \(a^2 - 6ab + 9b^2\) corresponde al producto notable \((a - 3b)^2\), lo que no se ajusta a la descripción geométrica de un área restante simple.
6. Multiplicando una Suma por una Diferencia de Binomios
Suma por Diferencia: Un Producto Notable Especial
Hemos visto cómo desarrollar el cuadrado de un binomio, tanto para la suma como para la resta. Ahora, vamos a explorar otro producto notable muy importante y útil: la suma por diferencia, que tiene la forma \((a + b)(a - b)\).
Desarrollo del Producto Notable (a + b)(a - b)
Para desarrollar la expresión \((a + b)(a - b)\), aplicamos la propiedad distributiva que ya conocemos. ¡Fíjate en lo que ocurre con los términos del medio!
\( (a + b)(a - b) = a \cdot (a - b) + b \cdot (a - b) \)
\( = a^2 - ab + ba - b^2 \)
Como \( -ab \) y \( +ba \) son términos iguales con signo opuesto, se anulan entre sí:
\( = a^2 - b^2 \)
El resultado es siempre la diferencia de los cuadrados de ambos términos:
\( (a + b)(a - b) = a^2 - b^2 \)
Se lee como: "el primer término al cuadrado, menos el segundo término al cuadrado".
Esta propiedad es excelente para calcular multiplicaciones difíciles mentalmente. Por ejemplo, para calcular \(28 \cdot 32\):
Podemos reescribirlo como \( (30 - 2)(30 + 2) \). Esto es una suma por diferencia.
El resultado es \( 30^2 - 2^2 = 900 - 4 = 896 \). ¡Mucho más fácil!
Ejercicios (Suma por Diferencia)
✨ Ejemplo Guiado (Nivel 1): Resolvamos \( (10 + 3)(10 - 3) \) usando la fórmula.
Aplicamos la fórmula \( (a+b)(a-b) = a^2 - b^2 \), donde \(a=10\) y \(b=3\).
Desarrollo: \( (10)^2 - (3)^2 \)
\( = 100 - 9 \)
\( = 91 \)
Comprobación: \( (10 + 3)(10 - 3) = (13) \cdot (7) = 91 \). ¡Funciona!
Nivel 1: Expandir con valores enteros.
Ejercicio 1: \( (3 + 2)(3 - 2) \)
Ejercicio 2: \( (5 + 1)(5 - 1) \)
Ejercicio 3: \( (7 + 4)(7 - 4) \)
Ejercicio 4: \( (6 + 3)(6 - 3) \)
R1: \( 3^2 - 2^2 = 9 - 4 = 5 \)
R2: \( 5^2 - 1^2 = 25 - 1 = 24 \)
R3: \( 7^2 - 4^2 = 49 - 16 = 33 \)
R4: \( 6^2 - 3^2 = 36 - 9 = 27 \)
✨ Ejemplo Guiado (Nivel 2): Resolvamos \( (2.5 + 0.5)(2.5 - 0.5) \) usando la fórmula.
Aplicamos la fórmula, donde \(a=2.5\) y \(b=0.5\).
Desarrollo: \( (2.5)^2 - (0.5)^2 \)
\( = 6.25 - 0.25 \)
\( = 6 \)
Comprobación: \( (2.5 + 0.5)(2.5 - 0.5) = (3) \cdot (2) = 6 \). ¡Correcto!
Nivel 2: Expandir con valores racionales.
Ejercicio 1: \( (1 + 0.5)(1 - 0.5) \)
Ejercicio 2: \( (\frac{3}{4} + \frac{1}{4})(\frac{3}{4} - \frac{1}{4}) \)
Ejercicio 3: \( (2\frac{1}{2} + 1)(2\frac{1}{2} - 1) \)
Ejercicio 4: \( (3.5 - 1.5)(3.5 + 1.5) \)
R1: \( 1^2 - 0.5^2 = 1 - 0.25 = 0.75 \)
R2: \( (\frac{3}{4})^2 - (\frac{1}{4})^2 = \frac{9}{16} - \frac{1}{16} = \frac{8}{16} = \frac{1}{2} \)
R3: \( (\frac{5}{2})^2 - 1^2 = \frac{25}{4} - 1 = \frac{21}{4} = 5.25 \)
R4: \( 3.5^2 - 1.5^2 = 12.25 - 2.25 = 10 \)
✨ Ejemplo Guiado (Nivel 3): Expandamos \( (5x + 2y)(5x - 2y) \).
Aquí, el primer término es \(a=5x\) y el segundo es \(b=2y\).
Aplicamos la fórmula: \( a^2 - b^2 \)
Desarrollo: \( (5x)^2 - (2y)^2 \)
Resultado: \( 25x^2 - 4y^2 \)
Nivel 3: Expandir con expresiones algebraicas.
1. \( (x + 2)(x - 2) \)
2. \( (a - 3)(a + 3) \)
3. \( (m + n)(m - n) \)
4. \( (2x + 1)(2x - 1) \)
5. \( (5 - 3y)(5 + 3y) \)
6. \( (\frac{1}{2}a + 2)(\frac{1}{2}a - 2) \)
7. \( (1.5 - 0.5x)(1.5 + 0.5x) \)
8. \( (x + y)(x - y) \)
9. \( (3a - 2b)(3a + 2b) \)
10. \( (m + \frac{1}{3})(m - \frac{1}{3}) \)
11. \( (2.5 - x)(2.5 + x) \)
12. \( (4x + 3y)(4x - 3y) \)
13. \( (\frac{2}{5}m - \frac{1}{2}n)(\frac{2}{5}m + \frac{1}{2}n) \)
14. \( (0.1x + 1)(0.1x - 1) \)
R1: \( x^2 - 4 \)
R2: \( a^2 - 9 \)
R3: \( m^2 - n^2 \)
R4: \( 4x^2 - 1 \)
R5: \( 25 - 9y^2 \)
R6: \( \frac{1}{4}a^2 - 4 \)
R7: \( 2.25 - 0.25x^2 \)
R8: \( x^2 - y^2 \)
R9: \( 9a^2 - 4b^2 \)
R10: \( m^2 - \frac{1}{9} \)
R11: \( 6.25 - x^2 \)
R12: \( 16x^2 - 9y^2 \)
R13: \( \frac{4}{25}m^2 - \frac{1}{4}n^2 \)
R14: \( 0.01x^2 - 1 \)
- En \((5x+...)(5x-...)\), el primer término al cuadrado es \((5x)^2 = 25x^2\), no \(5x^2\).
Factorizando una Diferencia de Cuadrados
Este es uno de los casos de factorización más importantes. Si identificas una expresión con dos términos que son cuadrados perfectos y que se están restando, puedes factorizarla como una suma por diferencia.
Para factorizar \(a^2 - b^2\), seguimos estos pasos:
- Verificar la forma: ¿Son solo dos términos? ¿Se están restando? ¿Ambos tienen raíz cuadrada exacta?
- Encontrar las raíces: Calcula la raíz cuadrada de cada término ( \(\sqrt{a^2}=a\) y \(\sqrt{b^2}=b\) ).
- Escribir el resultado: Escribe las dos raíces sumándose en un paréntesis y restándose en otro: \((a+b)(a-b)\).
✨ Ejemplo Guiado (Nivel 4): Factoricemos \( 36m^2 - 49n^2 \).
Paso 1: ¿Cumple la forma? Sí, son dos términos, se restan y ambos parecen tener raíz exacta.
Paso 2: Encontrar las raíces.
- La raíz de \(36m^2\) es \(6m\).
- La raíz de \(49n^2\) es \(7n\).
Paso 3: Escribir el resultado.
La factorización es \( (6m + 7n)(6m - 7n) \).
Nivel 4: Factorizar las siguientes diferencias de cuadrados.
1. \( x^2 - 4 \)
2. \( a^2 - 25 \)
3. \( m^2 - n^2 \)
4. \( 4x^2 - 1 \)
5. \( 16 - 9y^2 \)
6. \( \frac{1}{4}a^2 - 4 \)
7. \( 2.25 - 0.25x^2 \)
8. \( x^2 - y^2 \)
9. \( 9a^2 - 4b^2 \)
10. \( m^2 - \frac{1}{9} \)
11. \( 6.25 - x^2 \)
12. \( 16x^2 - 9y^2 \)
13. \( \frac{4}{25}m^2 - \frac{1}{4}n^2 \)
14. \( 0.01x^2 - 1 \)
R1: \( (x + 2)(x - 2) \)
R2: \( (a + 5)(a - 5) \)
R3: \( (m + n)(m - n) \)
R4: \( (2x + 1)(2x - 1) \)
R5: \( (4 + 3y)(4 - 3y) \)
R6: \( (\frac{1}{2}a + 2)(\frac{1}{2}a - 2) \)
R7: \( (1.5 + 0.5x)(1.5 - 0.5x) \)
R8: \( (x + y)(x - y) \)
R9: \( (3a + 2b)(3a - 2b) \)
R10: \( (m + \frac{1}{3})(m - \frac{1}{3}) \)
R11: \( (2.5 + x)(2.5 - x) \)
R12: \( (4x + 3y)(4x - 3y) \)
R13: \( (\frac{2}{5}m + \frac{1}{2}n)(\frac{2}{5}m - \frac{1}{2}n) \)
R14: \( (0.1x + 1)(0.1x - 1) \)
Problemas de Aplicación
✨ Ejemplo Guiado (Nivel 5): Un jardín rectangular tiene un área de \( (4x^2 - 25) \) metros cuadrados. Encuentra expresiones para su largo y su ancho.
Paso 1: Entender el problema.
Nos dan el área y nos piden las dimensiones (largo y ancho). Sabemos que Área = \(largo \cdot ancho\). La expresión del área es una resta de dos términos que parecen ser cuadrados perfectos.
Paso 2: Factorizar el área.
Debemos factorizar la diferencia de cuadrados \(4x^2 - 25\).
- La raíz de \(4x^2\) es \(2x\).
- La raíz de \(25\) es \(5\).
Respuesta: La factorización es \( (2x + 5)(2x - 5) \). Por lo tanto, el largo y el ancho del jardín pueden ser \( (2x + 5) \) metros y \( (2x - 5) \) metros.
Problema 1: El área de un rectángulo se puede expresar como \(x^2 - 16\) unidades cuadradas. Si la longitud y el ancho del rectángulo son de la forma \((x + k)\) y \((x - k)\), ¿cuáles son las expresiones para sus dimensiones?
Respuesta: Factorizando la expresión \(x^2 - 16\) como una diferencia de cuadrados, obtenemos \((x + 4)(x - 4)\). Por lo tanto, la longitud y el ancho del rectángulo pueden ser \((x + 4)\) y \((x - 4)\) unidades.
Problema 2 (Desafío): La diferencia entre el cuadrado de un número \((a)\) y el cuadrado de otro número \((b)\) es 100. Si la suma de ambos números \((a+b)\) es 20, ¿cuál es el valor de cada número?
Respuesta: Sabemos que \( a^2 - b^2 = 100 \). Factorizando, tenemos \( (a+b)(a-b) = 100 \). El problema nos dice que \(a+b = 20\). Reemplazamos en la ecuación: \( (20)(a-b) = 100 \). Despejando, \( a-b = 100/20 = 5 \). Ahora tenemos un sistema de ecuaciones:
1) a + b = 20
2) a - b = 5
Sumando ambas ecuaciones, obtenemos \(2a = 25\), por lo que \(a = 12.5\). Reemplazando en la primera ecuación, \(12.5 + b = 20\), por lo que \(b = 7.5\).
Problema 3: Se quiere diseñar una alfombra rectangular con un área que se puede expresar como \(9x^2 - 4y^2\) metros cuadrados. ¿Cuáles son las posibles expresiones para la longitud y el ancho de la alfombra en términos de 'x' e 'y'?
Respuesta: Factorizando la expresión \(9x^2 - 4y^2\) como una diferencia de cuadrados, obtenemos \((3x + 2y)(3x - 2y)\). Por lo tanto, las posibles expresiones para la longitud y el ancho de la alfombra son \((3x + 2y)\) metros y \((3x - 2y)\) metros.
7. Practica Integrada
Práctica Integrada: Productos Notables
¡Es hora de poner a prueba tus habilidades! En esta sección, encontrarás ejercicios que combinan todos los productos notables que hemos estudiado. El desafío es doble: primero, identificar qué caso tienes en frente y, segundo, resolverlo correctamente.
Para expandir:
- Cuadrado de Binomio (Suma): \( (a + b)^2 = a^2 + 2ab + b^2 \)
- Cuadrado de Binomio (Resta): \( (a - b)^2 = a^2 - 2ab + b^2 \)
- Suma por Diferencia: \( (a + b)(a - b) = a^2 - b^2 \)
Para factorizar:
- Trinomio Cuadrado Perfecto: \( a^2 \pm 2ab + b^2 = (a \pm b)^2 \)
- Diferencia de Cuadrados: \( a^2 - b^2 = (a + b)(a - b) \)
✨ Ejemplo Guiado (Nivel 1)
Parte A: Expandir \( (3x - 1)^2 \)
1. Identificar: Es un Cuadrado de Binomio (Resta), con \(a=3x\) y \(b=1\).
2. Aplicar fórmula \(a^2 - 2ab + b^2\):
\((3x)^2 - 2 \cdot (3x) \cdot 1 + (1)^2 \)
3. Resolver:
\(9x^2 - 6x + 1\)
Parte B: Factorizar \( y^2 - 100 \)
1. Identificar: Es una Diferencia de Cuadrados, con \(a^2=y^2\) y \(b^2=100\).
2. Encontrar raíces: La raíz de \(y^2\) es \(y\). La raíz de \(100\) es \(10\).
3. Aplicar fórmula \((a+b)(a-b)\):
\((y + 10)(y - 10)\)
Nivel 1: Identifica el producto notable y resuélvelo.
1. \((x + 3)^2\)
2. \((2a - 5)^2\)
3. \((m + n)(m - n)\)
4. \(9x^{2} - 4\)
5. \((3y + 7)^2\)
6. \((4p - q)^2\)
7. \((t + 9)(t - 9)\)
8. \(16 - y^{2}\)
9. \((0.5x + 1)^2\)
10. \((5 - 2y)^2\)
R1 – Cuadrado de Binomio (Suma):
\( (x + 3)^2 = x^2 + 2 \cdot x \cdot 3 + 3^2 = \boxed{x^2 + 6x + 9} \)
R2 – Cuadrado de Binomio (Resta):
\( (2a - 5)^2 = (2a)^2 - 2 \cdot 2a \cdot 5 + 5^2 = \boxed{4a^2 - 20a + 25} \)
R3 – Suma por Diferencia:
\( (m + n)(m - n) = \boxed{m^2 - n^2} \)
R4 – Diferencia de Cuadrados:
\( 9x^{2} - 4 = (3x)^2 - 2^2 = \boxed{(3x + 2)(3x - 2)} \)
R5 – Cuadrado de Binomio (Suma):
\( (3y + 7)^2 = (3y)^2 + 2 \cdot 3y \cdot 7 + 7^2 = \boxed{9y^2 + 42y + 49} \)
R6 – Cuadrado de Binomio (Resta):
\( (4p - q)^2 = (4p)^2 - 2 \cdot 4p \cdot q + q^2 = \boxed{16p^2 - 8pq + q^2} \)
R7 – Suma por Diferencia:
\( (t + 9)(t - 9) = t^2 - 9^2 = \boxed{t^2 - 81} \)
R8 – Diferencia de Cuadrados:
\( 16 - y^{2} = 4^2 - y^2 = \boxed{(4 + y)(4 - y)} \)
R9 – Cuadrado de Binomio (Suma):
\( (0.5x + 1)^2 = (0.5x)^2 + 2 \cdot 0.5x \cdot 1 + 1^2 = \boxed{0.25x^2 + x + 1} \)
R10 – Cuadrado de Binomio (Resta):
\( (5 - 2y)^2 = 5^2 - 2 \cdot 5 \cdot 2y + (2y)^2 = \boxed{4y^2 - 20y + 25} \)
✨ Ejemplo Guiado (Nivel 2): Resolvamos \( (x + 5)(x - 5) - (x + 2)^2 \).
Paso 1: Desarrollar cada producto notable por separado.
\( = (x^2 - 25) - (x^2 + 4x + 4) \)
Paso 2: Eliminar paréntesis (¡cuidado con el signo negativo!).
\( = x^2 - 25 - x^2 - 4x - 4 \)
Paso 3: Agrupar términos semejantes y simplificar.
\( = (x^2 - x^2) - 4x + (-25 - 4) \)
\( = \boxed{-4x - 29} \)
Nivel 2: Suma o resta y simplifica.
1. \((x + 2)^2 + (x - 2)^2\)
2. \((a + b)^2 - (a - b)^2\)
3. \((3y - 5)^2 + (3y + 5)^2\)
4. \((2m + n)(2m - n) + (m + n)^2\)
5. \((p + 4)^2 + (p - 4)^2\)
6. \((2q - 1)^2 - (2q + 1)^2\)
7. \((k + 3)(k - 3) + (k - 3)^2\)
8. \((5 - y)^2 + (5 + y)^2\)
9. \((x + 1)(x - 1) - (x - 1)^2\)
10. \((3a + 2b)^2 - (3a - 2b)^2\)
R1: \((x^2 + 4x + 4) + (x^2 - 4x + 4) = \boxed{2x^2 + 8}\)
R2: \((a^2 + 2ab + b^2) - (a^2 - 2ab + b^2) = \boxed{4ab}\)
R3: \((9y^2 - 30y + 25) + (9y^2 + 30y + 25) = \boxed{18y^2 + 50}\)
R4: \((4m^2 - n^2) + (m^2 + 2mn + n^2) = \boxed{5m^2 + 2mn}\)
R5: \((p^2 + 8p + 16) + (p^2 - 8p + 16) = \boxed{2p^2 + 32}\)
R6: \((4q^2 - 4q + 1) - (4q^2 + 4q + 1) = \boxed{-8q}\)
R7: \((k^2 - 9) + (k^2 - 6k + 9) = \boxed{2k^2 - 6k}\)
R8: \((25 - 10y + y^2) + (25 + 10y + y^2) = \boxed{2y^2 + 50}\)
R9: \((x^2 - 1) - (x^2 - 2x + 1) = \boxed{2x - 2}\)
R10: \((9a^2 + 12ab + 4b^2) - (9a^2 - 12ab + 4b^2) = \boxed{24ab}\)
✨ Ejemplo Guiado (Nivel 3): Resolvamos \( 2(a + 3)^2 - 3(a + 1)(a - 1) \).
Paso 1: Desarrollar los productos notables (aún dentro de paréntesis).
\( = 2(a^2 + 6a + 9) - 3(a^2 - 1) \)
Paso 2: Aplicar la propiedad distributiva con los coeficientes.
\( = (2a^2 + 12a + 18) - (3a^2 - 3) \)
Paso 3: Eliminar paréntesis y simplificar.
\( = 2a^2 + 12a + 18 - 3a^2 + 3 \)
\( = \boxed{-a^2 + 12a + 21} \)
Nivel 3: Desarrolla y simplifica cada expresión.
1. \(3(x - 2)^2 - 2(x + 1)^2\)
2. \(4(a + b)(a - b) - (a - b)^2\)
3. \(5(2y - 3)^2 + (2y + 3)(2y - 3)\)
4. \(2(x - y)^2 - (x + y)^2\)
5. \((x + 4)(x - 4) + 2(x + 4)^2\)
6. \(3(a - 2)^2 - 4(a + 2)(a - 2)\)
7. \(4(2m + 1)^2 + (2m - 1)^2 - 8m^2\)
8. \(6(y - 1)^2 - 3(y + 1)^2\)
9. \((p + q)^2 - 2(p - q)^2\)
10. \(4(0.5x - 1)^2 + (0.5x + 1)^2\)
R1: \(3(x^2 - 4x + 4) - 2(x^2 + 2x + 1) = \boxed{x^2 - 16x + 10}\)
R2: \(4(a^2 - b^2) - (a^2 - 2ab + b^2) = \boxed{3a^2 + 2ab - 5b^2}\)
R3: \(5(4y^2 - 12y + 9) + (4y^2 - 9) = \boxed{24y^2 - 60y + 36}\)
R4: \(2(x^2 - 2xy + y^2) - (x^2 + 2xy + y^2) = \boxed{x^2 - 6xy + y^2}\)
R5: \((x^2 - 16) + 2(x^2 + 8x + 16) = \boxed{3x^2 + 16x + 16}\)
R6: \(3(a^2 - 4a + 4) - 4(a^2 - 4) = \boxed{-a^2 - 12a + 28}\)
R7: \(4(4m^2 + 4m + 1) + (4m^2 - 4m + 1) - 8m^2 = \boxed{12m^2 + 12m + 5}\)
R8: \(6(y^2 - 2y + 1) - 3(y^2 + 2y + 1) = \boxed{3y^2 - 18y + 3}\)
R9: \((p^2 + 2pq + q^2) - 2(p^2 - 2pq + q^2) = \boxed{-p^2 + 6pq - q^2}\)
R10: \(4(0.25x^2 - x + 1) + (0.25x^2 + x + 1) = \boxed{1.25x^2 - 3x + 5}\)
✨ Ejemplo Guiado (Nivel 4): Factoricemos \( 3x^2 - 12 \).
Paso 1: Buscar siempre un factor común primero.
\( = 3(x^2 - 4) \)
Paso 2: Identificar el producto notable dentro del paréntesis.
\( (x^2 - 4) \) es una Diferencia de Cuadrados.
Paso 3: Factorizar y mantener el factor común.
\( = 3(x + 2)(x - 2) \)
\( = \boxed{3(x + 2)(x - 2)} \)
Nivel 4: Reconoce el tipo de factorización y factoriza.
1. \(x^{2} + 12x + 36\)
2. \(4x^{2} - 25\)
3. \(9a^{2} - 6ab + b^{2}\)
4. \(16m^{2} - 8m + 1\)
5. \(y^{2} - 49\)
6. \(25p^{2} + 20p + 4\)
7. \(36z^{2} - 64\)
8. \(a^{2} - 2a + 1\)
9. \(49k^{2} - 36\)
10. \(0.04x^{2} - 0.08x + 0.04\)
R1 - TCP Suma:
\(x^2 + 12x + 36 = \boxed{(x+6)^2}\)
R2 - Diferencia de Cuadrados:
\(4x^2 - 25 = \boxed{(2x+5)(2x-5)}\)
R3 - TCP Resta:
\(9a^2 - 6ab + b^2 = \boxed{(3a-b)^2}\)
R4 - TCP Resta:
\(16m^2 - 8m + 1 = \boxed{(4m-1)^2}\)
R5 - Diferencia de Cuadrados:
\(y^2 - 49 = \boxed{(y+7)(y-7)}\)
R6 - TCP Suma:
\(25p^2 + 20p + 4 = \boxed{(5p+2)^2}\)
R7 - Factor Común + Dif. de Cuadrados:
\(36z^2 - 64 = 4(9z^2 - 16) = \boxed{4(3z+4)(3z-4)}\)
R8 - TCP Resta:
\(a^2 - 2a + 1 = \boxed{(a-1)^2}\)
R9 - Diferencia de Cuadrados:
\(49k^2 - 36 = \boxed{(7k+6)(7k-6)}\)
R10 - Factor Común + TCP Resta:
\(0.04x^2 - 0.08x + 0.04 = 0.04(x^2-2x+1) = \boxed{0.04(x-1)^2}\)
8. Aplicando Productos Notables en Diversos Contextos
Aplicando los Productos Notables a Situaciones Concretas
Ahora que ya hemos estudiado y practicado los tres productos notables principales, vamos a aplicarlos en la resolución de problemas. Estas situaciones nos ayudarán a comprender la verdadera utilidad de estas herramientas en diferentes contextos, especialmente en la geometría y el cálculo.
Para expandir:
- Cuadrado de Binomio (Suma): \( (a + b)^2 = a^2 + 2ab + b^2 \)
- Cuadrado de Binomio (Resta): \( (a - b)^2 = a^2 - 2ab + b^2 \)
- Suma por Diferencia: \( (a + b)(a - b) = a^2 - b^2 \)
Para factorizar:
- Trinomio Cuadrado Perfecto: \( a^2 \pm 2ab + b^2 = (a \pm b)^2 \)
- Diferencia de Cuadrados: \( a^2 - b^2 = (a + b)(a - b) \)
Enfrenta cada problema con este plan de 4 pasos:
- Leer y Visualizar: Entiende qué te piden. Si es un problema geométrico, haz un dibujo simple.
- Traducir al Álgebra: Convierte los datos del problema en una expresión matemática.
- Identificar el Producto Notable: Observa la expresión. ¿A cuál de las fórmulas se parece?
- Resolver y Simplificar: Aplica la fórmula del producto notable y simplifica el resultado final.
Ejercicios
Nivel 1: Problemas de geometría que involucren el cálculo de áreas.
✨ Ejemplo Guiado (Nivel 1): Un jardín cuadrado tiene un lado que mide \( (2x - 1) \) metros. ¿Cuál es la expresión que representa su área?
1. Visualizar: Imaginamos un cuadrado con lado \( (2x-1) \).
2. Traducir al Álgebra: El área de un cuadrado es \(lado^2\). La expresión es \( (2x - 1)^2 \).
3. Identificar: La expresión es un Cuadrado de Binomio (Resta), con \(a=2x\) y \(b=1\).
4. Resolver: Aplicamos la fórmula \(a^2 - 2ab + b^2\):
\( (2x)^2 - 2 \cdot (2x) \cdot 1 + (1)^2 \)
\( = 4x^2 - 4x + 1 \)
Respuesta: El área del jardín es \( (4x^2 - 4x + 1) \) metros cuadrados.
Problema 1: Calcula el área de un cuadrado cuyo lado mide \( (x + 5) \) unidades.
Respuesta: El área es \( (x + 5)^2 \). Aplicando el cuadrado de un binomio (suma), obtenemos: \( x^2 + 2 \cdot x \cdot 5 + 5^2 = \boxed{x^2 + 10x + 25} \) unidades cuadradas.
Problema 2: Un rectángulo tiene una base que mide \( (2x - 3) \) unidades y una altura que mide \( (2x + 3) \) unidades. Calcula el área del rectángulo.
Respuesta: El área es \( (2x - 3)(2x + 3) \). Aplicando la suma por diferencia, obtenemos: \( (2x)^2 - 3^2 = \boxed{4x^2 - 9} \) unidades cuadradas.
Problema 3: Encuentra la expresión para el área de un cuadrado cuyo lado mide \( (3x - 2y) \) unidades.
Respuesta: El área es \( (3x - 2y)^2 \). Aplicando el cuadrado de un binomio (resta), obtenemos: \( (3x)^2 - 2 \cdot 3x \cdot 2y + (2y)^2 = \boxed{9x^2 - 12xy + 4y^2} \) unidades cuadradas.
Problema 4: Un rectángulo tiene una base que mide \( (x + 4) \) unidades y una altura que mide \( (x - 4) \) unidades. Calcula el área del rectángulo.
Respuesta: El área es \( (x + 4)(x - 4) \). Aplicando la suma por diferencia, obtenemos: \( x^2 - 4^2 = \boxed{x^2 - 16} \) unidades cuadradas.
Nivel 2: Problemas que combinen el cálculo de áreas con la suma o resta de otras áreas.
✨ Ejemplo Guiado (Nivel 2): Un salón de eventos cuadrado tiene un lado de \( (x+10) \) metros. En el centro, se instala una pista de baile cuadrada de lado \( (x-10) \) metros. ¿Qué área del salón queda disponible para las mesas?
1. Visualizar: Un cuadrado grande con un cuadrado más pequeño en su interior.
2. Traducir al Álgebra: Nos piden el área restante, que es (Área Salón) - (Área Pista).
La expresión es \( (x+10)^2 - (x-10)^2 \).
3. Identificar y Resolver: Desarrollamos cada cuadrado de binomio.
Área Salón: \( (x+10)^2 = x^2 + 20x + 100 \)
Área Pista: \( (x-10)^2 = x^2 - 20x + 100 \)
4. Simplificar: Restamos las expresiones (¡cuidado con los paréntesis!).
\( (x^2 + 20x + 100) - (x^2 - 20x + 100) \)
\( = x^2 + 20x + 100 - x^2 + 20x - 100 \)
\( = \boxed{40x} \)
Respuesta: El área disponible para las mesas es de \( 40x \) metros cuadrados.
Problema 1: Se tiene un cuadrado de lado \( (x + 2) \) metros. En el centro, se construye una fuente cuadrada de lado 'x' metros. Calcula el área restante del cuadrado que no está ocupada por la fuente.
Respuesta: Área grande: \( (x + 2)^2 = x^2 + 4x + 4 \). Área fuente: \( x^2 \).
Área restante: \( (x^2 + 4x + 4) - x^2 = \boxed{4x + 4} \) metros cuadrados.
Problema 2: Se quiere pintar una pared rectangular de \( (3x + 1) \) metros de largo y \( (3x - 1) \) metros de ancho. En la pared hay una ventana cuadrada de lado 'x' metros que no se pintará. Calcula el área de la pared que se pintará.
Respuesta: Área pared: \( (3x + 1)(3x - 1) = 9x^2 - 1 \). Área ventana: \( x^2 \).
Área a pintar: \( (9x^2 - 1) - x^2 = \boxed{8x^2 - 1} \) metros cuadrados.
Problema 3: Un marco de fotos cuadrado tiene un lado exterior que mide \( (2x + 3) \) cm. El marco tiene un ancho uniforme de 2 cm. Calcula el área visible de la foto (el área interior del marco).
Respuesta: El lado interior se calcula restando dos veces el ancho del marco al lado exterior: \( (2x + 3) - 2 - 2 = (2x - 1) \) cm. El área visible es el área del cuadrado interior: \( (2x - 1)^2 = \boxed{4x^2 - 4x + 1} \) cm².
Problema 4: Se tiene un terreno cuadrado de lado \( (4x + 5) \) metros. Se quiere construir una casa cuadrada en el centro, dejando un jardín alrededor. Si el lado de la casa mide \( (2x + 1) \) metros, ¿cuál es el área del jardín?
Respuesta: Área terreno: \( (4x + 5)^2 = 16x^2 + 40x + 25 \). Área casa: \( (2x + 1)^2 = 4x^2 + 4x + 1 \).
Área jardín: \( (16x^2 + 40x + 25) - (4x^2 + 4x + 1) = \boxed{12x^2 + 36x + 24} \) metros cuadrados.
Nivel 3: Problemas de aplicación a situaciones cotidianas.
✨ Ejemplo Guiado (Nivel 3): Una artesana fabrica cajas de madera cuadradas. El costo de los materiales por caja es de \( (x-2)^2 \) pesos. El precio de venta de cada caja es de \( (x+2)(x-2) \) pesos. ¿Qué expresión representa su ganancia por caja?
1. Visualizar: Necesitamos calcular Ganancia = Venta - Costo.
2. Traducir y Resolver:
Precio Venta: \( (x+2)(x-2) = x^2 - 4 \)
Costo Materiales: \( (x-2)^2 = x^2 - 4x + 4 \)
3. Simplificar la Ganancia:
Ganancia = \( (x^2 - 4) - (x^2 - 4x + 4) \)
\( = x^2 - 4 - x^2 + 4x - 4 \)
\( = \boxed{4x - 8} \)
Respuesta: La ganancia por cada caja es de \( (4x - 8) \) pesos.
Problema 1: Una empresa produce baldosas cuadradas. El costo de producción de cada baldosa, según la longitud de su lado 'x', es de \( (x + 3)^2 \) pesos. Si la empresa vende cada baldosa a \( (x + 5)^2 \) pesos, ¿cuál es la expresión que representa la ganancia por baldosa?
Respuesta: Ganancia = Venta - Costo = \( (x + 5)^2 - (x + 3)^2 \).
Esto es una diferencia de cuadrados: \( ((x+5)+(x+3))((x+5)-(x+3)) \)
\( = (2x+8)(2) = \boxed{4x + 16} \) pesos.
Problema 2: Se quiere cercar un jardín rectangular con una valla. El largo del jardín es \( (x + 7) \) metros y el ancho es \( (x - 7) \) metros. Si el costo de la valla es de $10.000 por metro, ¿cuál es la expresión para el costo total de cercar el jardín?
Respuesta: El perímetro es \( 2 \cdot (\text{largo} + \text{ancho}) = 2 \cdot ((x + 7) + (x - 7)) = 2 \cdot (2x) = 4x \) metros. El costo total es \( 4x \cdot 10000 = \boxed{40000x} \) pesos.
Problema 3: Un capital de \( (x + 100) \) pesos se invierte a un interés compuesto anual del 10%. ¿Cuál es la expresión que representa el monto total después de 2 años?
Respuesta: Después de 2 años, el monto es \( (x + 100) \cdot (1.10)^2 \).
Desarrollando: \( (x + 100) \cdot (1.21) = \boxed{1.21x + 121} \) pesos.
Problema 4 (Análisis Crítico): Se realiza una encuesta a \( (2x - 5) \) personas. La cantidad de personas que responden "sí" es \( (x + 5) \) y las que responden "no" es \( (x - 10) \). ¿Es esta situación siempre posible?
Respuesta: La suma de los que dicen "sí" y "no" debe ser igual al total de encuestados: \( (x+5) + (x-10) = 2x - 5 \).
Simplificando el lado izquierdo: \( 2x - 5 = 2x - 5 \).
La igualdad se cumple, pero para que la situación sea posible, la cantidad de personas en cada grupo no puede ser negativa. El grupo "no", \( (x - 10) \), sería negativo si \(x < 10\). Por lo tanto, la situación solo es posible si \(x \ge 10\).
9. Complemento Avanzados: Estrategias Avanzadas con Productos Notables
Estrategias Avanzadas con Productos Notables
En esta página final, aplicaremos todo lo aprendido para resolver expresiones complejas. La clave ya no es solo aplicar una fórmula, sino desarrollar una visión algebraica: aprender a reconocer patrones familiares dentro de problemas más grandes y de varios pasos.
Para expandir:
- \( (a + b)^2 = a^2 + 2ab + b^2 \)
- \( (a - b)^2 = a^2 - 2ab + b^2 \)
- \( (a + b)(a - b) = a^2 - b^2 \)
Para factorizar:
- \( a^2 \pm 2ab + b^2 = (a \pm b)^2 \)
- \( a^2 - b^2 = (a + b)(a - b) \)
El secreto en los ejercicios avanzados es tratar a los productos notables como "bloques". A veces, un binomio entero como \((x+5)\) puede ser el término 'a' de una fórmula más grande. ¡Busca siempre la estructura general primero!
Ejercicios
✨ Ejemplo Guiado (Nivel 1): Resolvamos \( (a + 2)(a - 2) - (a - 3)^2 \)
1. Identificar y desarrollar cada producto notable por separado:
Suma por diferencia: \( (a+2)(a-2) = a^2 - 4 \)
Cuadrado de binomio: \( (a-3)^2 = a^2 - 6a + 9 \)
2. Reemplazar en la expresión original (¡usando paréntesis!):
\( (a^2 - 4) - (a^2 - 6a + 9) \)
3. Eliminar paréntesis y simplificar:
\( = a^2 - 4 - a^2 + 6a - 9 \)
\( = \boxed{6a - 13} \)
Nivel 1: Desarrollo de expresiones algebraicas.
Ejercicio 1: \( (x + 2)^2 + (x - 2)^2 \)
Ejercicio 2: \( (a + 3)(a - 3) - (a + 1)^2 \)
Ejercicio 3: \( 2(m + 4)^2 - 3(m + 1)(m - 1) \)
Ejercicio 4: \( (2x + y)^2 - (2x - y)^2 \)
R1: \( (x^2 + 4x + 4) + (x^2 - 4x + 4) = \boxed{2x^2 + 8} \)
R2: \( (a^2 - 9) - (a^2 + 2a + 1) = a^2 - 9 - a^2 - 2a - 1 = \boxed{-2a - 10} \)
R3: \( 2(m^2 + 8m + 16) - 3(m^2 - 1) = 2m^2 + 16m + 32 - 3m^2 + 3 = \boxed{-m^2 + 16m + 35} \)
R4: \( (4x^2 + 4xy + y^2) - (4x^2 - 4xy + y^2) = \boxed{8xy} \)
✨ Ejemplo Guiado (Nivel 2): Factoricemos \( a^2 + 2ab + b^2 - c^2 \).
1. Agrupar para reconocer un patrón: Los primeros tres términos parecen un Trinomio Cuadrado Perfecto.
\( (a^2 + 2ab + b^2) - c^2 \)
2. Factorizar el patrón conocido:
\( = (a + b)^2 - c^2 \)
3. Reconocer el NUEVO patrón: ¡Ahora tenemos una Diferencia de Cuadrados! Donde el primer término es \((a+b)\) y el segundo es \(c\).
4. Aplicar la segunda factorización \((A^2 - B^2) = (A+B)(A-B)\):
\( = [(a+b) + c][(a+b) - c] \)
\( = \boxed{(a+b+c)(a+b-c)} \)
Nivel 2: Factorización de expresiones compuestas.
Ejercicio 1: \( x^2 + 10x + 25 - y^2 \)
Ejercicio 2: \( 4a^2 - 12a + 9 - b^2 \)
Ejercicio 3: \( m^2 - n^2 + 2n - 1 \)
Ejercicio 4: \( 9x^2 - 16y^2 + 8y - 1 \)
R1: \( (x^2 + 10x + 25) - y^2 = (x + 5)^2 - y^2 = \boxed{(x + 5 + y)(x + 5 - y)} \)
R2: \( (4a^2 - 12a + 9) - b^2 = (2a - 3)^2 - b^2 = \boxed{(2a - 3 + b)(2a - 3 - b)} \)
R3: \( m^2 - (n^2 - 2n + 1) = m^2 - (n - 1)^2 = \boxed{(m + n - 1)(m - n + 1)} \)
R4: \( 9x^2 - (16y^2 - 8y + 1) = (3x)^2 - (4y - 1)^2 = \boxed{(3x + 4y - 1)(3x - 4y + 1)} \)
✨ Ejemplo Guiado (Nivel 3): Dos Caminos hacia la Solución
Problema: \( (x + 1)^2 + 2(x + 1)(x - 1) + (x - 1)^2 \)
Método 1: Fuerza Bruta (El Camino Seguro)
Desarrollamos cada producto notable por separado y luego simplificamos.
Paso 1: \( \underbrace{(x^2 + 2x + 1)}_{(x+1)^2} + \underbrace{2(x^2 - 1)}_{2(x+1)(x-1)} + \underbrace{(x^2 - 2x + 1)}_{(x-1)^2} \)
Paso 2: \( = x^2 + 2x + 1 + 2x^2 - 2 + x^2 - 2x + 1 \)
Paso 3: \( = (x^2+2x^2+x^2) + (2x-2x) + (1-2+1) \)
Resultado: \( = \boxed{4x^2} \)
Método 2: Visión Algebraica (El Camino Elegante)
Paso 1: Reconocer el patrón general. La expresión tiene la forma \(A^2 + 2AB + B^2\).
Donde: \( A = (x+1) \) y \( B = (x-1) \)
Paso 2: Factorizar usando el patrón. Sabemos que \(A^2 + 2AB + B^2 = (A+B)^2\).
Paso 3: Reemplazar A y B de vuelta y simplificar.
\( = ((x+1) + (x-1))^2 \)
\( = (x+1+x-1)^2 \)
\( = (2x)^2 \)
Resultado: \( = \boxed{4x^2} \)
Nivel 3: Desarrolla y simplifica. Para cada ejercicio, la solución mostrará dos métodos: el tradicional ("Fuerza Bruta") y uno más rápido usando visión algebraica ("Técnica Avanzada"). ¡Compara ambos caminos!
1. \( (x + 1)^2 + 2(x + 1)(x - 1) + (x - 1)^2 \)
2. \( (a + b)^2 - 2(a + b)(a - b) + (a - b)^2 \)
3. \( 3(x - 2)^2 + 2(x + 1)(x - 1) - (x + 3)^2 \)
4. \( (a + b + c)^2 - (a + b - c)^2 \)
5. \( (x + y + 2)(x + y - 2) - (x + y)^2 \)
6. \( (2a - b)^2 + 2(2a - b)(a + b) + (a + b)^2 \)
Respuesta 1:
Método 1 (Fuerza Bruta):
\( = (x^2 + 2x + 1) + 2(x^2 - 1) + (x^2 - 2x + 1) \)
\( = x^2 + 2x + 1 + 2x^2 - 2 + x^2 - 2x + 1 \)
\( = \boxed{4x^2} \)
Método 2 (Técnica Avanzada):
Reconocemos la forma \(A^2 + 2AB + B^2 = (A+B)^2\), donde \(A=(x+1)\) y \(B=(x-1)\).
\( = ((x+1) + (x-1))^2 = (x+1+x-1)^2 = (2x)^2 = \boxed{4x^2} \)
Respuesta 2:
Método 1 (Fuerza Bruta):
\( = (a^2 + 2ab + b^2) - 2(a^2 - b^2) + (a^2 - 2ab + b^2) \)
\( = a^2 + 2ab + b^2 - 2a^2 + 2b^2 + a^2 - 2ab + b^2 \)
\( = \boxed{4b^2} \)
Método 2 (Técnica Avanzada):
Reconocemos la forma \(A^2 - 2AB + B^2 = (A-B)^2\), donde \(A=(a+b)\) y \(B=(a-b)\).
\( = ((a+b) - (a-b))^2 = (a+b-a+b)^2 = (2b)^2 = \boxed{4b^2} \)
Respuesta 3:
Método 1 (Fuerza Bruta):
\( = 3(x^2 - 4x + 4) + 2(x^2 - 1) - (x^2 + 6x + 9) \)
\( = 3x^2 - 12x + 12 + 2x^2 - 2 - x^2 - 6x - 9 \)
\( = \boxed{4x^2 - 18x + 1} \)
Método 2 (Técnica Avanzada):
En este caso, no hay un atajo claro que simplifique toda la expresión. El método de fuerza bruta es el más directo y apropiado.
Respuesta 4:
Método 1 (Fuerza Bruta):
\( = (a^2+b^2+c^2+2ab+2ac+2bc) - (a^2+b^2+c^2+2ab-2ac-2bc) \)
\( = a^2+b^2+c^2+2ab+2ac+2bc - a^2-b^2-c^2-2ab+2ac+2bc \)
\( = \boxed{4ac + 4bc} \)
Método 2 (Técnica Avanzada):
Reconocemos la forma \(A^2 - B^2 = (A+B)(A-B)\), donde \(A=(a+b+c)\) y \(B=(a+b-c)\).
\( = ((a+b+c) + (a+b-c)) \cdot ((a+b+c) - (a+b-c)) \)
\( = (2a+2b) \cdot (2c) = \boxed{4c(a+b)} \)
Respuesta 5:
Método 1 (Fuerza Bruta):
\( = (x(x+y-2)+y(x+y-2)+2(x+y-2)) - (x^2+2xy+y^2) \)
\( = (x^2+xy-2x+xy+y^2-2y+2x+2y-4) - (x^2+2xy+y^2) \)
\( = (x^2+2xy+y^2-4) - x^2-2xy-y^2 = \boxed{-4} \)
Método 2 (Técnica Avanzada):
Reconocemos \( (x+y+2)(x+y-2) \) como una Suma por Diferencia \((A+B)(A-B)\), donde \(A=(x+y)\) y \(B=2\).
\( = ((x+y)^2 - 2^2) - (x+y)^2 \)
\( = (x+y)^2 - 4 - (x+y)^2 = \boxed{-4} \)
Respuesta 6:
Método 1 (Fuerza Bruta):
\( = (4a^2-4ab+b^2) + 2(2a^2+2ab-ab-b^2) + (a^2+2ab+b^2) \)
\( = (4a^2-4ab+b^2) + 2(2a^2+ab-b^2) + (a^2+2ab+b^2) \)
\( = 4a^2-4ab+b^2 + 4a^2+2ab-2b^2 + a^2+2ab+b^2 = \boxed{9a^2} \)
Método 2 (Técnica Avanzada):
Reconocemos la forma \(A^2 + 2AB + B^2 = (A+B)^2\), donde \(A=(2a-b)\) y \(B=(a+b)\).
\( = ((2a-b) + (a+b))^2 = (2a-b+a+b)^2 = (3a)^2 = \boxed{9a^2} \)
✨ Ejemplo Guiado (Nivel 4): Simplifiquemos \( \frac{(a+b)^2 - (a-b)^2}{4ab} \)
1. Enfocarse en el numerador y desarrollarlo:
\( (a+b)^2 - (a-b)^2 = (a^2+2ab+b^2) - (a^2-2ab+b^2) \)
2. Simplificar el numerador:
\( = a^2+2ab+b^2 - a^2+2ab-b^2 = 4ab \)
3. Reemplazar y simplificar la fracción:
\( = \frac{4ab}{4ab} = \boxed{1} \)
Nivel 4: Simplificación de expresiones racionales.
1. \( \frac{(x + 2)^2 - (x - 2)^2}{4x} \)
2. \( \frac{(a + b)^2 - (a - b)^2}{ab} \)
3. \( \frac{(2m + 1)^2 - (2m - 1)^2}{2m} \)
4. \( \frac{(x+y)^2-(x-y)^2}{(x-y)^2-(x+y)^2} \)
R1: \( \frac{8x}{4x} = \boxed{2} \)
R2: \( \frac{4ab}{ab} = \boxed{4} \)
R3: \( \frac{8m}{2m} = \boxed{4} \)
R4: \( \frac{4xy}{-4xy} = \boxed{-1} \)
Problemas de Aplicación Avanzada
✨ Ejemplo Guiado (Nivel 5): Un cuadrado tiene un lado de \( (x+3) \) cm. Se construye un nuevo cuadrado aumentando el lado en 2 cm. ¿Cuál es la expresión que representa el aumento de área?
1. Área Original: \( A_1 = (x+3)^2 = x^2+6x+9 \)
2. Lado Nuevo: \( L_2 = (x+3)+2 = x+5 \)
3. Área Nueva: \( A_2 = (x+5)^2 = x^2+10x+25 \)
4. Aumento de Área (Área Nueva - Área Original):
\( (x^2+10x+25) - (x^2+6x+9) \)
\( = x^2+10x+25 - x^2-6x-9 \)
\( = \boxed{4x+16} \)
Respuesta: El área aumentó en \( (4x+16) \) cm².
Nivel 5: Situaciones problemáticas de varios pasos.
Problema 1: Un terreno rectangular tiene un largo de \( (x+5) \) metros y un ancho de \( (x-5) \) metros. Si se aumenta el largo en 3 metros y se disminuye el ancho en 3 metros, ¿cuál es la diferencia entre el área original y el área nueva?
Respuesta: Área original: \( (x+5)(x-5) = x^2 - 25 \).
Nuevas dimensiones: largo \(x+8\), ancho \(x-8\).
Área nueva: \( (x+8)(x-8) = x^2 - 64 \).
Diferencia: \( (x^2-25) - (x^2-64) = \boxed{39} \) metros cuadrados.
Problema 2: Se tiene un cuadrado de lado \( (2x + 1) \) cm. Si se aumenta cada lado en 2 cm, ¿cuál es la expresión que representa el aumento en el área del cuadrado?
Respuesta: Área original: \( (2x+1)^2 = 4x^2+4x+1 \).
Nuevo lado: \( (2x+1)+2 = 2x+3 \).
Área nueva: \( (2x+3)^2 = 4x^2+12x+9 \).
Aumento: \( (4x^2+12x+9) - (4x^2+4x+1) = \boxed{8x+8} \) cm².
Problema 3: Un depósito de agua cúbico tiene una arista de \( (x+1) \) metros. El costo de construcción es de $10.000 por metro cuadrado de superficie. ¿Cuál es la expresión que representa el costo total?
Respuesta: El área de una cara del cubo es \( (x+1)^2 \). Un cubo tiene 6 caras, así que el área total es \( 6(x+1)^2 = 6(x^2+2x+1) = 6x^2+12x+6 \).
Costo total: \( 10000 \cdot (6x^2+12x+6) = \boxed{60000x^2 + 120000x + 60000} \) pesos.
10. Complemento Avanzados: Completando el Cuadrado: ¡Transformando Expresiones!
Completando el Cuadrado: ¡Transformando Expresiones!
En las páginas anteriores, hemos trabajado con trinomios cuadrados perfectos, que son el resultado de elevar un binomio al cuadrado. Ahora, vamos a aprender una técnica llamada "completar el cuadrado" que nos permite forzar a casi cualquier expresión cuadrática a adoptar esta forma tan útil.
Para transformar una expresión de la forma \(x^2 + bx\), sigue estos pasos:
- Identificar 'b': Es el coeficiente que acompaña a la 'x'.
- Calcular el "término mágico": Divide 'b' entre 2 y elévalo al cuadrado. El término es \( (\frac{b}{2})^2 \).
- Sumar y Restar: Suma y resta este término a la expresión. Al sumar cero (ej. "+9 - 9"), no alteramos su valor.
- Factorizar y Simplificar: Agrupa los tres primeros términos para formar el trinomio cuadrado perfecto y simplifica el resto.
La principal utilidad de esta técnica es reescribir una función cuadrática \(ax^2+bx+c\) en su forma vértice: \(a(x-h)^2 + k\).
En esta forma, el punto \((h, k)\) es el vértice de la parábola, lo que nos dice inmediatamente el valor máximo o mínimo de la expresión. ¡Es una herramienta fundamental para problemas de optimización!
Ejercicios (Completando el Cuadrado)
✨ Ejemplo Guiado (Nivel 1): Completemos el cuadrado para \(x^2 - 2x\).
1. Identificar 'b': Aquí, \(b = -2\).
2. Calcular término mágico: \( (\frac{-2}{2})^2 = (-1)^2 = 1 \).
3. Sumar y Restar: \( = x^2 - 2x + 1 - 1 \)
4. Factorizar y Simplificar: El trinomio \(x^2 - 2x + 1\) se factoriza como \((x-1)^2\).
\( = \boxed{(x - 1)^2 - 1} \)
Nivel 1: Completar el cuadrado en expresiones de la forma \(x^2 + bx\).
1. \( x^2 + 4x \)
2. \( x^2 + 10x \)
3. \( x^2 - 8x \)
4. \( x^2 - 3x \)
R1: \( x^2 + 4x + 4 - 4 = \boxed{(x + 2)^2 - 4} \)
R2: \( x^2 + 10x + 25 - 25 = \boxed{(x + 5)^2 - 25} \)
R3: \( x^2 - 8x + 16 - 16 = \boxed{(x - 4)^2 - 16} \)
R4: \( x^2 - 3x + \frac{9}{4} - \frac{9}{4} = \boxed{(x - \frac{3}{2})^2 - \frac{9}{4}} \)
✨ Ejemplo Guiado (Nivel 2): Completemos el cuadrado para \(x^2 + 4x - 5\).
1. Identificar 'b': \(b = 4\).
2. Calcular término mágico: \( (\frac{4}{2})^2 = 2^2 = 4 \).
3. Sumar y Restar (y agrupar el término 'c' al final):
\( = (x^2 + 4x + 4) - 4 - 5 \)
4. Factorizar y Simplificar:
\( = \boxed{(x + 2)^2 - 9} \)
Nivel 2: Completar el cuadrado en expresiones de la forma \(x^2 + bx + c\).
1. \( x^2 + 8x + 10 \)
2. \( x^2 - 6x + 5 \)
3. \( x^2 + 5x + 2 \)
4. \( x^2 - 2x - 3 \)
R1: \( (x^2 + 8x + 16) - 16 + 10 = \boxed{(x + 4)^2 - 6} \)
R2: \( (x^2 - 6x + 9) - 9 + 5 = \boxed{(x - 3)^2 - 4} \)
R3: \( (x^2 + 5x + \frac{25}{4}) - \frac{25}{4} + 2 = \boxed{(x + \frac{5}{2})^2 - \frac{17}{4}} \)
R4: \( (x^2 - 2x + 1) - 1 - 3 = \boxed{(x - 1)^2 - 4} \)
✨ Ejemplo Guiado (Nivel 3): Completemos el cuadrado para \(2x^2 + 12x + 10\).
1. Factorizar el coeficiente principal (2) de los términos con x:
\( = 2(x^2 + 6x) + 10 \)
2. Completar el cuadrado DENTRO del paréntesis (\(b=6 \rightarrow (\frac{6}{2})^2=9\)):
\( = 2(x^2 + 6x + 9 - 9) + 10 \)
3. Sacar el término sobrante (-9) del paréntesis, multiplicándolo por el 2 de afuera:
\( = 2(x^2 + 6x + 9) - 18 + 10 \)
4. Factorizar y simplificar:
\( = \boxed{2(x + 3)^2 - 8} \)
Nivel 3: Completar el cuadrado cuando el coeficiente principal es distinto de 1.
1. \( 2x^2 + 4x + 5 \)
2. \( 3x^2 - 9x + 6 \)
3. \( -x^2 - 6x + 2 \)
4. \( 4x^2 - 8x - 1 \)
5. \( \frac{1}{2}x^2 + x + 2 \)
6. \( -2x^2 + 10x - 7 \)
R1: \( 2(x^2+2x) + 5 = 2(x+1)^2-2+5 = \boxed{2(x+1)^2+3} \)
R2: \( 3(x^2-3x) + 6 = 3(x-\frac{3}{2})^2-\frac{27}{4}+6 = \boxed{3(x-\frac{3}{2})^2-\frac{3}{4}} \)
R3: \( -(x^2+6x) + 2 = -(x+3)^2+9+2 = \boxed{-(x+3)^2+11} \)
R4: \( 4(x^2-2x) - 1 = 4(x-1)^2-4-1 = \boxed{4(x-1)^2-5} \)
R5: \( \frac{1}{2}(x^2+2x) + 2 = \frac{1}{2}(x+1)^2-\frac{1}{2}+2 = \boxed{\frac{1}{2}(x+1)^2+\frac{3}{2}} \)
R6: \( -2(x^2-5x) - 7 = -2(x-\frac{5}{2})^2+\frac{25}{2}-7 = \boxed{-2(x-\frac{5}{2})^2+\frac{11}{2}} \)
Problemas de Aplicación (Máximos y Mínimos)
✨ Ejemplo Guiado (Nivel 5): Los ingresos \(I\), en miles de pesos, de una tienda están dados por la función \(I(x) = -x^2 + 10x + 50\), donde \(x\) es el número de productos vendidos. Encuentra el número de productos que maximiza el ingreso y cuál es ese ingreso máximo.
1. Reescribir completando el cuadrado:
\( I(x) = -(x^2 - 10x) + 50 \)
\( = -(x^2 - 10x + 25 - 25) + 50 \)
\( = -( (x-5)^2 - 25 ) + 50 \)
\( = -(x-5)^2 + 25 + 50 \)
\( = -(x-5)^2 + 75 \)
2. Analizar la forma vértice: La expresión tiene la forma \(a(x-h)^2+k\). Como el término \(-(x-5)^2\) siempre será negativo o cero, el valor máximo de \(I(x)\) se alcanza cuando \((x-5)^2\) es cero.
3. Concluir:
Esto ocurre cuando \(x=5\).
El ingreso máximo es el valor que queda, es decir, \(75\).
Respuesta: Se deben vender 5 productos para obtener un ingreso máximo de $75.000 pesos.
Nivel 5: Situaciones problemáticas que involucren completar el cuadrado.
Problema 1: La altura 'h' (en metros) de un proyectil en función del tiempo 't' (en segundos) está dada por \(h(t) = -5t^2 + 20t + 10\). ¿Cuál es la altura máxima que alcanza y en qué segundo ocurre?
Respuesta: Completando el cuadrado: \(h(t) = -5(t^2 - 4t) + 10 = -5(t-2)^2 + 20 + 10 = \boxed{-5(t - 2)^2 + 30}\). La altura máxima es de 30 metros y ocurre a los 2 segundos.
Problema 2: Una empresa determina que la ganancia 'G' (en miles de pesos) por vender 'x' unidades está modelada por \(G(x) = -2x^2 + 12x - 8\). ¿Cuántas unidades deben venderse para maximizar la ganancia y cuál es esa ganancia máxima?
Respuesta: Completando el cuadrado: \(G(x) = -2(x^2 - 6x) - 8 = -2(x-3)^2 + 18 - 8 = \boxed{-2(x-3)^2 + 10}\). Se deben vender 3 unidades para una ganancia máxima de $10.000 pesos.
Problema 3: El costo 'C' (en pesos) de producir 'x' artículos está dado por \(C(x) = x^2 - 8x + 20\). ¿Cuántos artículos se deben producir para minimizar el costo y cuál es ese costo mínimo?
Respuesta: Completando el cuadrado: \(C(x) = (x^2 - 8x + 16) - 16 + 20 = \boxed{(x - 4)^2 + 4}\). Se deben producir 4 artículos para un costo mínimo de $4 pesos.