Homotecia - Página 1: Introducción y Proporcionalidad

Introducción

Imagina que tienes una linterna y proyectas la sombra de un objeto en la pared. Si acercas o alejas el objeto de la linterna, la sombra cambia de tamaño, ¿verdad? Eso es, en esencia, una homotecia. Es una transformación geométrica que "amplía" o "reduce" figuras, pero manteniendo su forma original. Piensa en ella como un "zoom" geométrico. La homotecia se define por un centro (como la linterna en nuestro ejemplo) y un factor (que nos dice cuánto agrandamos o achicamos), y está muy relacionada con la idea de proporcionalidad, que ya conoces.

Definición

Formalmente, decimos que una homotecia \(H_{O,k}\) es una transformación que, a partir de un punto fijo llamado centro (que llamaremos \(O\)), y un número llamado factor de homotecia (que llamaremos \(k\)), transforma cualquier punto \(P\) en otro punto \(P'\) que cumple dos condiciones:

1. \(O\), \(P\), y \(P'\) están en la misma línea recta. Es decir, si dibujas una línea que pasa por \(O\) y \(P\), el punto \(P'\) también estará en esa línea.
2. La distancia entre \(O\) y \(P'\) (que escribimos como \(OP'\)) es igual a la distancia entre \(O\) y \(P\) (que escribimos como \(OP\)) multiplicada por el valor absoluto de \(k\) (que escribimos como \(|k|\)). En símbolos: \(OP' = |k| \cdot OP\).

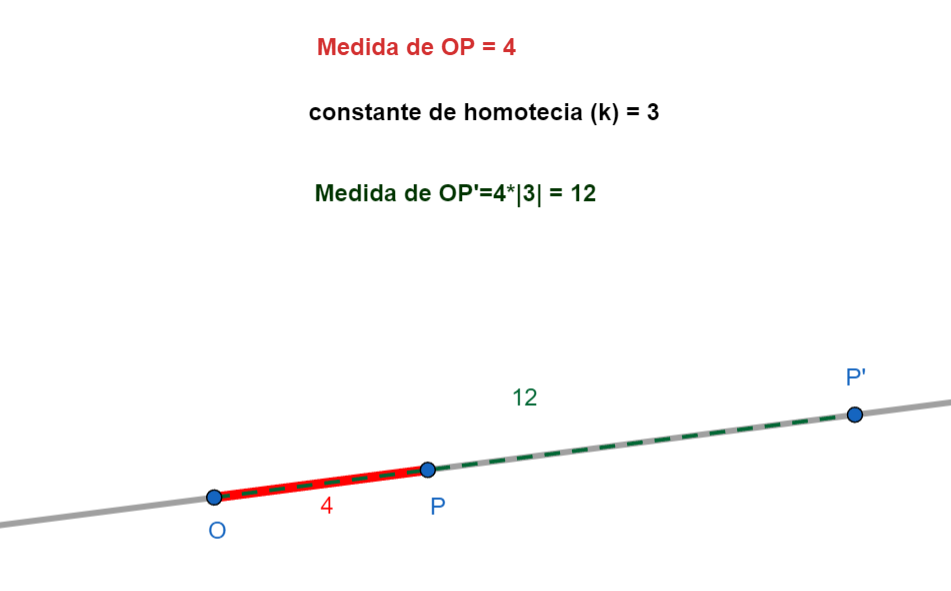
Importante: Si \(k\) es positivo, \(P'\) está en la misma dirección que \(P\) respecto a \(O\). Si \(k\) es negativo, \(P'\) está en la dirección *opuesta* a \(P\) respecto a \(O\). Imagina que la figura se "da vuelta" a través del centro.

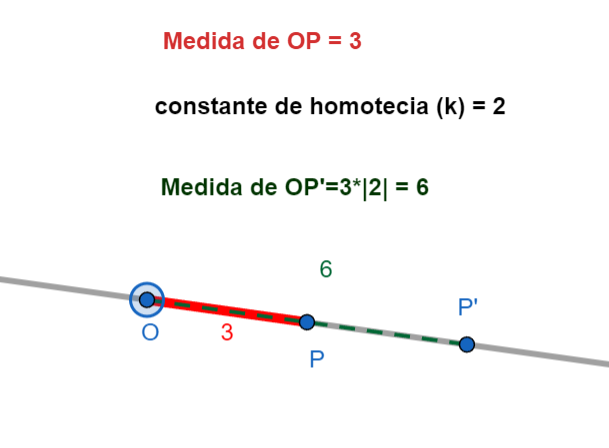
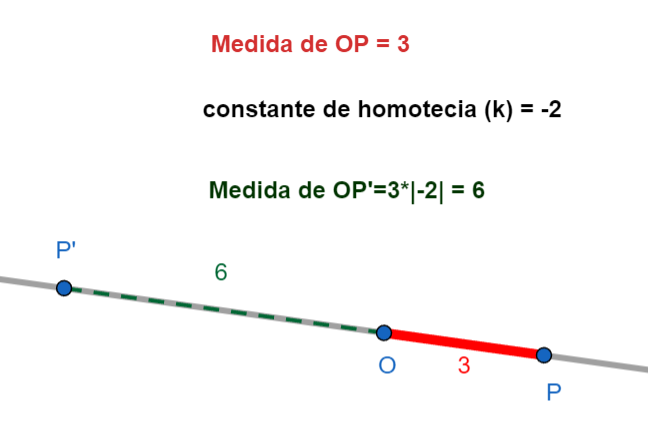
Elementos Clave

Para entender bien la homotecia, hay tres conceptos fundamentales:

• Centro \(O\): Es como el punto de origen de la transformación, el punto desde donde "estiramos" o "encogemos" la figura. Es el único punto que no se mueve en la homotecia.
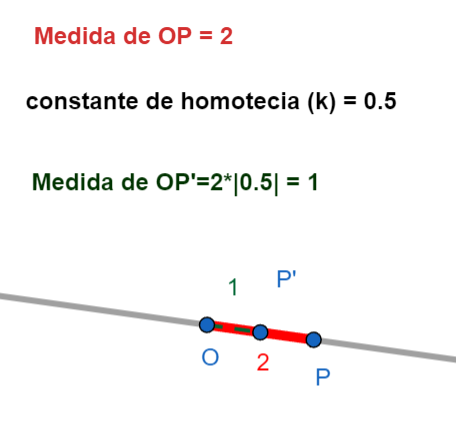
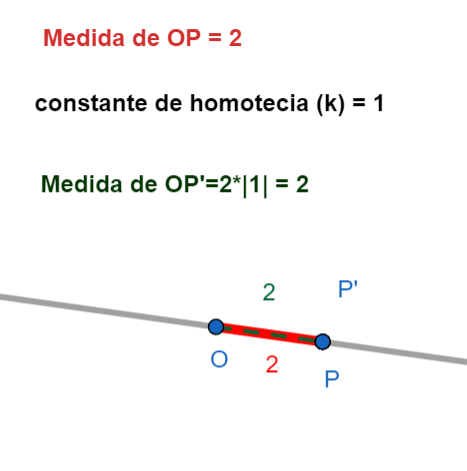
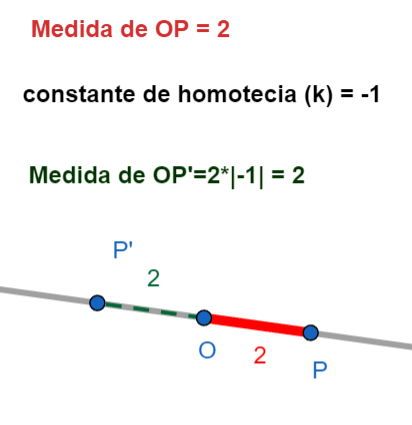
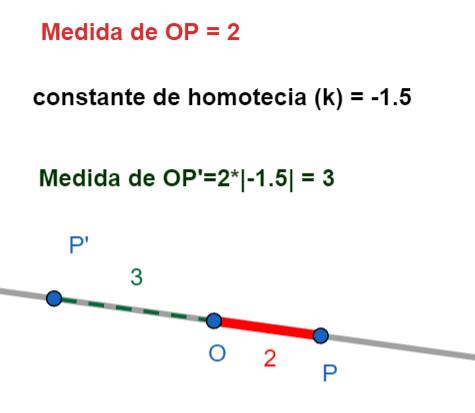
• Factor \(k\): Es un número que nos dice cuánto se agranda o se achica la figura.

	Si \(|k| > 1\), la figura se *agranda*. Por ejemplo, si \(k = 2\), la figura resultante será el doble de grande que la original.
	Si \(0 < |k| < 1\), la figura se *reduce*. Por ejemplo, si \(k = 0.5\) (o \(k = \frac{1}{2}\)), la figura resultante será la mitad de la original.
	Si \(k = 1\), la figura no cambia de tamaño. \(P\) y \(P'\) son el mismo punto.
	Si \(k = -1\), la figura se refleja con respecto al punto \(O\), y se mantiene del mismo tamaño.
	Si \(k\) es negativo, además de agrandar o achicar, la figura se *invierte* respecto al centro \(O\).

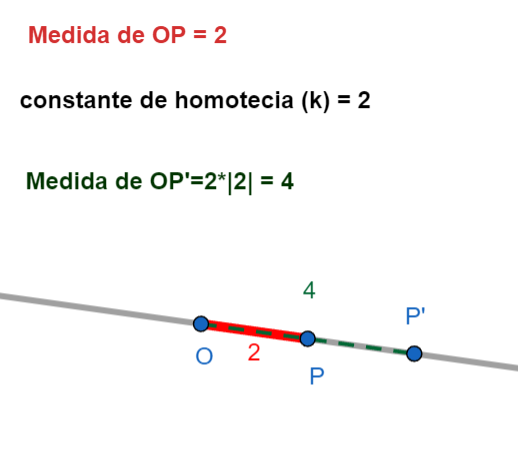• Conservación de Ángulos y Proporcionalidad: La homotecia es especial porque:
  • Los ángulos de la figura *no cambian*. Si tenías un triángulo rectángulo, seguirá siendo rectángulo después de la homotecia.
  • Las longitudes de los lados *sí cambian*, pero lo hacen de forma proporcional. Todos los lados se multiplican por el mismo factor \(|k|\). Esto significa que la razón entre dos lados de la figura original es la misma que la razón entre los lados correspondientes en la figura transformada.
  • 
    

Ejemplos

Ejemplo 1: Ampliación

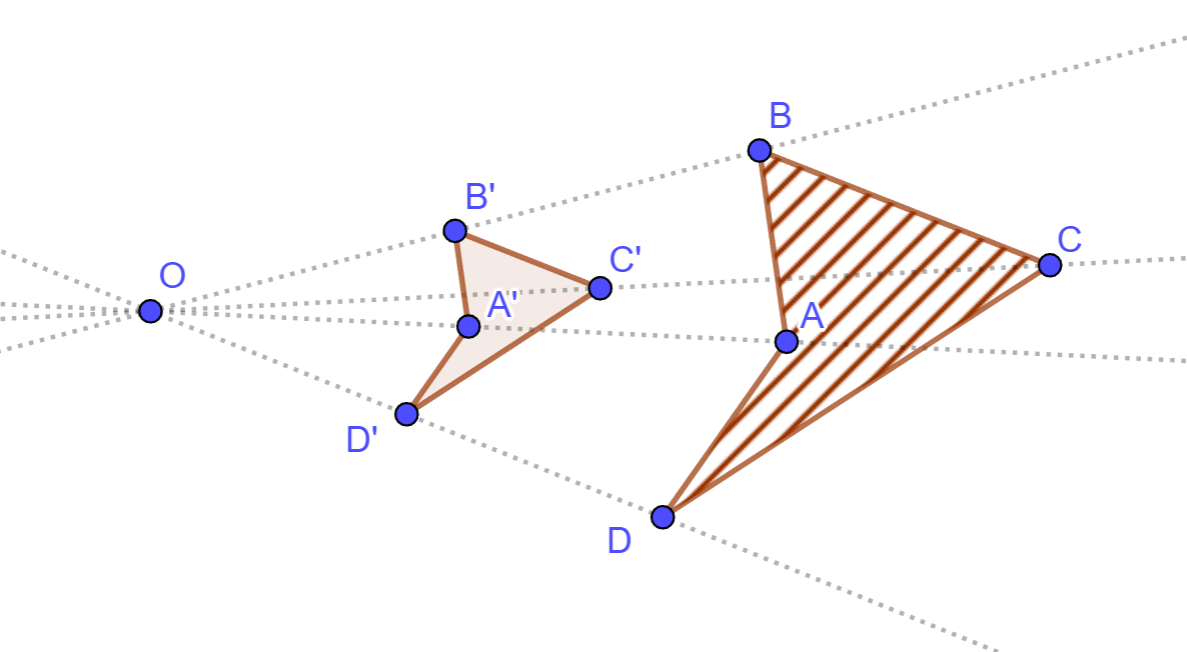
Tenemos un triángulo \(ABC\). Elegimos un punto \(O\) como centro de homotecia y un factor \(k = 2\). Para encontrar la imagen de cada vértice (los puntos \(A\), \(B\), y \(C\)), hacemos lo siguiente:

1. Dibujamos una línea recta desde \(O\) hasta \(A\).
2. Medimos la distancia \(OA\).
3. Multiplicamos esa distancia por 2 (porque \(k = 2\)).
4. Marcamos un punto \(A'\) sobre la línea \(OA\), pero a una distancia \(2 \cdot OA\) de \(O\).
5. Repetimos los pasos para los puntos \(B\) y \(C\), obteniendo \(B'\) y \(C'\).
6. Unimos \(A'\), \(B'\) y \(C'\) para obtener el triángulo \(A'B'C'\), que es el doble de grande que \(ABC\).

Ejemplo 2: Reducción e Inversión

Ahora, supongamos que tenemos un cuadrado y aplicamos una homotecia con centro \(O\) y factor \(k = -\frac{1}{2}\). Esto significa dos cosas:

• La figura se va a reducir a la mitad (porque \(|k| = \frac{1}{2}\)).
• La figura se va a invertir respecto a \(O\) (porque \(k\) es negativo).

Para construir la imagen, seguimos los mismos pasos que antes, pero al medir la distancia desde \(O\) a cada vértice, la dividimos entre 2 y marcamos el nuevo punto *al otro lado* de \(O\).

Ejemplo 3 (cotidiano): Una lupa. Cuando usas una lupa, estás aplicando una homotecia. El centro de la homotecia está aproximadamente en el centro de la lupa, y el factor de homotecia es mayor que 1 (por eso ves las cosas más grandes).

Práctica

Ahora vamos a practicar con algunos ejercicios. Los primeros tres son para que pienses en los conceptos, y los siguientes siete son para que apliques lo aprendido con dibujos y cálculos. Al final, hay cuatro problemas más desafiantes. ¡No te preocupes si al principio te cuesta, la práctica hace al maestro!

Ejercicios

1. (Conceptual) ¿Qué significa el factor de homotecia? Explica con tus propias palabras qué pasa si el factor es mayor que 1, y qué pasa si está entre 0 y 1. ¿Qué pasa si es negativo?

   Solución: El factor de homotecia, \(k\), es como el "control de zoom" de la transformación. Nos dice cuánto más grande o más pequeña será la figura transformada en comparación con la original.

   • Si \(|k| > 1\), la figura se agranda. Es como usar una lupa.
   • Si \(0 < |k| < 1\), la figura se reduce. Es como alejar un objeto: lo vemos más pequeño.
   • Si \(k\) es negativo, la figura se invierte respecto al centro \(O\), además de agrandarse o achicarse. Imagina que la figura "cruza" el centro y se da vuelta.
2. (Conceptual) La homotecia hace que las figuras cambien de tamaño, pero *no* cambia su forma. ¿Por qué?

   Solución: La forma de una figura está determinada por sus ángulos y por las *proporciones* entre sus lados. La homotecia conserva los ángulos (los deja iguales) y, aunque cambia el tamaño de los lados, los cambia a todos *en la misma proporción* (todos se multiplican por el mismo número, \(|k|\)). Como las proporciones se mantienen, la forma general no cambia.

3. (Conceptual) En la definición de homotecia, se dice que los puntos \(O\), \(P\), y \(P'\) están *alineados*. ¿Qué significa esto, y por qué es importante?

   Solución: Que estén alineados significa que los tres puntos están sobre la misma línea recta. Esto es importante porque nos dice que la transformación se hace "directamente hacia afuera" o "directamente hacia adentro" desde el centro \(O\). Cada punto y su imagen están conectados por una línea que pasa por el centro.

4. (Práctica) Dibuja un cuadrado de lado 2 cm en tu cuaderno. Luego, elige un punto fuera del cuadrado (ese será tu centro \(O\)). Aplica una homotecia con factor \(k = 3\). ¿Cuánto mide el lado del nuevo cuadrado?

   Solución:

   1. Desde el centro \(O\), traza líneas rectas que pasen por cada uno de los vértices del cuadrado original.
   2. Mide la distancia desde \(O\) a cada vértice.
   3. Multiplica cada una de esas distancias por 3 (porque \(k = 3\)).
   4. Marca los nuevos vértices (las imágenes) a esas distancias *triplicadas*, sobre las líneas que ya dibujaste.
   5. Une los nuevos vértices para formar el cuadrado ampliado.

   El lado del nuevo cuadrado medirá \(2 \text{ cm} \times 3 = 6 \text{ cm}\).

5. (Práctica) Piensa en objetos tecnologicos de la vida real. ¿Puedes nombrar uno que porduzca un  resultados similares a crear una homotecia con \(k > 1\)? Explica por qué.

   Solución: Un proyector de diapositivas o de cine es un buen ejemplo. La imagen pequeña en la diapositiva (o en el archivo digital) se agranda mucho al proyectarse en la pantalla. La lámpara del proyector actúa como el centro de homotecia, y la distancia entre la lámpara y la pantalla determina el factor de ampliación. Otro ejemplo es una lupa: la lupa (centro de la homotecia) agranda la imagen del objeto que estás observando.

6. (Práctica) Tienes un triángulo. Quieres construir su imagen con una homotecia de factor \(k = \frac{1}{2}\), usando regla y compás. Describe paso a paso cómo lo harías.

   Solución:

   1. Elige un punto cualquiera como centro \(O\).
   2. Dibuja líneas rectas desde \(O\) hasta cada uno de los vértices del triángulo (llamémoslos \(A\), \(B\), y \(C\)).
   3. Mide la distancia \(OA\).
   4. Divide esa distancia entre 2 (porque \(k = \frac{1}{2}\)).
   5. Marca un punto \(A'\) sobre la línea \(OA\), a la distancia \(OA/2\) de \(O\).
   6. Repite los pasos 3, 4 y 5 para los puntos \(B\) y \(C\), obteniendo \(B'\) y \(C'\).
   7. Une \(A'\), \(B'\), y \(C'\) para formar el triángulo reducido. Este triángulo será exactamente la mitad del tamaño del original, y estará en la misma orientación.
7. (Práctica) Un punto \(P\) está a 5 cm de un punto \(O\). Aplicamos una homotecia con centro \(O\) y factor \(k = 2\). ¿A qué distancia de \(O\) quedará el punto imagen \(P'\)?

   Solución: La distancia \(OP'\) será igual a la distancia \(OP\) multiplicada por \(|k|\). En este caso, \(OP' = 5 \text{ cm} \times 2 = 10 \text{ cm}\). El punto \(P'\) quedará a 10 cm de \(O\).

8. (Práctica) Imagina que aplicas una homotecia a una figura usando un factor \(k = 0\). ¿Qué le pasa a la figura? Explica y da un ejemplo sencillo.

   Solución: Si \(k = 0\), *todos* los puntos de la figura se transforman en el centro \(O\). La figura "desaparece" o, más precisamente, se colapsa en un solo punto. Por ejemplo, si tienes un triángulo \(ABC\) y aplicas una homotecia con centro \(O\) y \(k = 0\), los puntos \(A'\), \(B'\), y \(C'\) *todos* coincidirán con \(O\). El triángulo se convierte en un punto.

9. (Práctica) Dibuja dos líneas rectas que se crucen en un punto \(O\). Marca un punto \(P\) en una de las líneas. Ahora, aplica una homotecia con centro \(O\) y factor \(k = -2\). Describe cómo encontrarías la posición del punto imagen \(P'\).

   Solución:

   1. Mide la distancia \(OP\).
   2. Multiplica esa distancia por 2 (porque \(|k| = 2\)).
   3. Como \(k\) es negativo, \(P'\) estará en la *dirección opuesta* a \(P\) respecto a \(O\). Es decir, \(P'\) estará en la misma línea que \(O\) y \(P\), pero *al otro lado* de \(O\).
   4. Marca el punto \(P'\) a una distancia \(2 \cdot OP\) de \(O\), pero en el lado opuesto a \(P\).
10. (Práctica) Piensa en un experimento donde usas una linterna para proyectar la sombra de un objeto (por ejemplo, un bloque de madera) sobre una pared. ¿De qué manera determinarías en este experimento el factor de homotecia de la sombra?

    Solución: En este experimento, la linterna es el centro de homotecia. El factor de homotecia está determinado por la *relación entre las distancias*. Específicamente:

    • Distancia de la linterna al objeto (bloque).
    • Distancia de la linterna a la pared.

    Si llamamos \(d_1\) a la distancia de la linterna al objeto, y \(d_2\) a la distancia de la linterna a la pared, entonces el valor absoluto del factor de homotecia es \(|k| = \frac{d_2}{d_1}\). Si la pared está más lejos de la linterna que el objeto (\(d_2 > d_1\)), entonces \(|k| > 1\) y la sombra será más grande que el objeto. Si acercas el objeto a la linterna (disminuyendo \(d_1\)), la sombra también se agranda.

Problemas

Estos problemas son un poco más difíciles. ¡Intenta resolverlos usando todo lo que has aprendido!

1. Un triángulo \(ABC\) tiene sus vértices a las siguientes distancias del centro de homotecia \(O\): \(OA = 3\) cm, \(OB = 4\) cm, y \(OC = 5\) cm. Si aplicamos una homotecia con centro \(O\) y factor \(k = 2\), ¿a qué distancias de \(O\) quedarán los vértices del triángulo transformado (\(A'\), \(B'\), y \(C'\))?

   Solución: Como el factor de homotecia es 2, todas las distancias desde el centro se duplican. Por lo tanto:

   • \(OA' = 2 \cdot OA = 2 \cdot 3 \text{ cm} = 6 \text{ cm}\)
   • \(OB' = 2 \cdot OB = 2 \cdot 4 \text{ cm} = 8 \text{ cm}\)
   • \(OC' = 2 \cdot OC = 2 \cdot 5 \text{ cm} = 10 \text{ cm}\)

   Los vértices del triángulo transformado quedarán a 6 cm, 8 cm y 10 cm de \(O\), respectivamente.

2. Dibuja un ejemplo de una homotecia con factor \(k = -3\). Elige una figura sencilla (como un triángulo o un cuadrado) y un centro de homotecia \(O\). Muestra claramente cómo la figura se agranda y se invierte.

   Solución (Guía):

   1. Dibuja un triángulo (o cuadrado) en tu cuaderno.
   2. Elige un punto \(O\) como centro de homotecia. Puede estar dentro o fuera de la figura, pero para que la inversión se vea más clara, es mejor elegirlo fuera.
   3. Dibuja líneas rectas desde \(O\) hasta cada uno de los vértices de la figura original.
   4. Mide la distancia desde \(O\) a cada vértice.
   5. Multiplica cada una de esas distancias por 3 (porque \(|k| = 3\)).
   6. Como \(k\) es negativo, marca los nuevos vértices (las imágenes) a esas distancias *triplicadas*, pero *al otro lado* de \(O\), sobre las líneas que ya dibujaste.
   7. Une los nuevos vértices para formar la figura transformada. Verás que la figura es tres veces más grande que la original y está "dada vuelta" con respecto a \(O\).
3. Un compañero de clase dice que "la homotecia cambia la forma de un rectángulo". ¿Cómo le demostrarías, con medidas y un ejemplo, que está equivocado?

   Solución: Para demostrar que la homotecia *no* cambia la forma, necesitamos mostrar que los ángulos se mantienen iguales y que las proporciones entre los lados también se mantienen. Podemos hacer lo siguiente:

   1. Dibuja un rectángulo. Mide sus ángulos (todos deben ser de 90 grados). Mide la longitud de sus lados (largo y ancho).
   2. Calcula la *razón* entre el largo y el ancho del rectángulo original (divide el largo entre el ancho).
   3. Aplica una homotecia al rectángulo (elige un centro \(O\) y un factor \(k\), por ejemplo, \(k = 2\)).
   4. Mide los ángulos del rectángulo transformado (deberían seguir siendo de 90 grados).
   5. Mide los lados del rectángulo transformado.
   6. Calcula la razón entre el largo y el ancho del rectángulo transformado. Esta razón debe ser *igual* a la razón que calculaste en el paso 2.

   Si los ángulos se mantienen y la razón entre los lados se mantiene, entonces la forma no ha cambiado; solo el tamaño.

4. En un plano, un punto \(P\) está a 2.5 cm de un punto \(O\). Primero, aplicamos una homotecia con centro \(O\) y factor \(k = 4\). Luego, al resultado de *esa* homotecia, le aplicamos *otra* homotecia, también con centro \(O\), pero con factor \(k = \frac{1}{4}\). ¿Dónde termina el punto \(P\) después de estas dos transformaciones?

   Solución:

   *Primera homotecia:* Después de la primera homotecia, el punto \(P\) se transforma en un punto \(P'\) que está a una distancia \(OP' = 2.5 \text{ cm} \times 4 = 10 \text{ cm}\) de \(O\).

   *Segunda homotecia:* Ahora, aplicamos una homotecia a \(P'\) con factor \(\frac{1}{4}\). El punto resultante, llamémoslo \(P''\), estará a una distancia \(OP'' = 10 \text{ cm} \times \frac{1}{4} = 2.5 \text{ cm}\) de \(O\).

   ¡El punto \(P''\) está en la misma posición que el punto original \(P\)! Esto sucede porque las dos homotecias "se cancelan" entre sí. Multiplicar por 4 y luego por \(\frac{1}{4}\) es lo mismo que multiplicar por 1.

Homotecia - Página 2: Homotecia en la Vida Diaria

Introducción

La homotecia no es solo algo que vemos en los libros de matemáticas. ¡Está a nuestro alrededor! Desde cómo funciona una lupa hasta cómo se forman las sombras, la homotecia está presente en muchas situaciones cotidianas. En esta página, exploraremos algunos ejemplos para que veas cómo este concepto matemático se aplica al mundo real.

Observaciones sobre Homotecia en lo Cotidiano

La homotecia aparece en muchos fenómenos que involucran luz y visión:

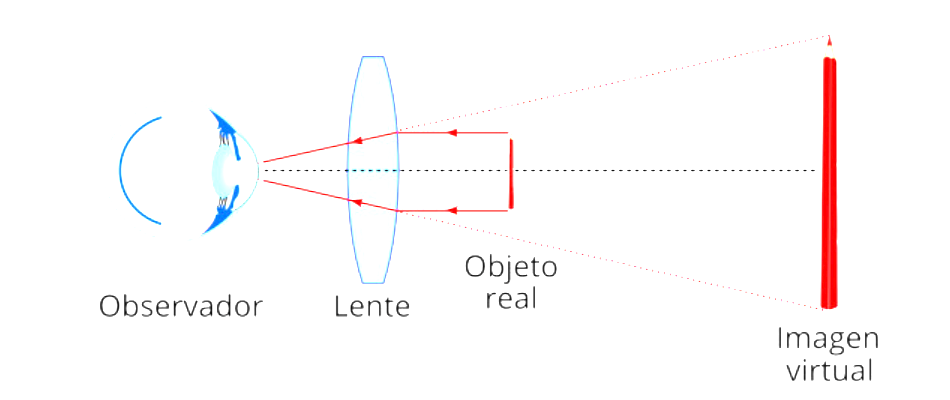
• Lupas: Cuando usas una lupa, estás aplicando una homotecia. La lupa actúa como el centro de la homotecia, y el factor de homotecia es mayor que 1 (por eso ves las cosas más grandes). La imagen que ves es una versión *ampliada* del objeto real.

• Sin la lupa, ves la hormiga con su tamaño normal.
• Al usar la lupa, la imagen que se forma es una homotecia del objeto original, con un factor de escala $k$ que depende de la distancia a la lente y la curvatura de esta.
• La hormiga sigue manteniendo sus proporciones (ángulos y forma), pero su tamaño aparente es mayor.

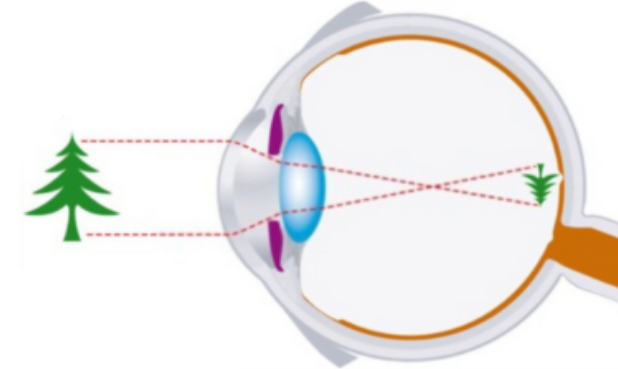
• El ojo humano: ¡Tu propio ojo es un sistema homotético! La luz entra por la pupila y el cristalino (que actúa como una lente) la enfoca en la retina, en la parte posterior del ojo. La imagen que se forma en la retina es una versión *reducida* e *invertida* del objeto que estás mirando. En términos de homotecia, el cristalino es el centro, y el factor de homotecia es menor que 1 (y negativo, porque la imagen está invertida).

• Sombras: Cuando la luz de una lámpara (o del sol) incide sobre un objeto, se crea una sombra. Esta sombra es, en esencia, una homotecia. La fuente de luz es el centro de homotecia, y el tamaño de la sombra depende de la distancia entre la fuente de luz, el objeto y la superficie donde se proyecta la sombra (como una pared o el suelo), 

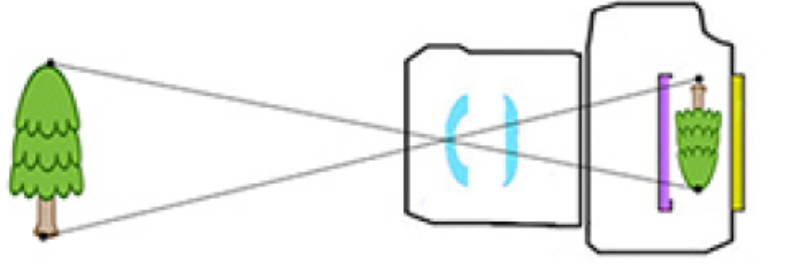
• Cámaras Fotográficas Una cámara fotográfica funciona de manera muy similar al ojo humano. La lente de la cámara (objetivo) actúa como centro de homotecia, enfocando la luz en el sensor (o la película, en cámaras antiguas). La imagen capturada es una versión reducida de la escena real.

• Proyectores: Un proyector de diapositivas, de cine o un proyector digital funcionan de manera opuesta a una cámara. La fuente de luz dentro del proyector es el centro de homotecia, y la imagen en la diapositiva (o en el chip digital) se *amplía* al proyectarse en la pantalla.

Elementos Clave en las Aplicaciones

En estos ejemplos, podemos identificar los elementos clave de la homotecia:

• Centro de homotecia: Generalmente es la fuente de luz (como una lámpara o el sol), una lente (como la de una lupa, el cristalino del ojo o la lente de una cámara), o un punto de convergencia (como el punto de fuga en un dibujo en perspectiva).
• Factor de homotecia (\(k\)): Está determinado por las distancias relativas entre la fuente de luz (o lente), el objeto y la superficie donde se forma la imagen (retina, pared, pantalla, etc.).
  • Si la imagen es más grande que el objeto, \(|k| > 1\).
  • Si la imagen es más pequeña que el objeto, \(0 < |k| < 1\).
  • Si la imagen está invertida con respecto al objeto, \(k\) es negativo.
• Aplicaciones: Cualquier situación donde veas rayos de luz que parecen emanar de un punto, o donde una imagen se forma a través de una lente, puede ser analizada (al menos aproximadamente) usando la idea de homotecia.

Ejemplos Visuales

Ejemplo 1: La lupa (Ampliación)

(Nota: La imagen "lupa_homotecia.png" debería mostrar un diagrama simple de una lupa, un objeto pequeño y una imagen virtual más grande).

Cuando acercas un objeto a una lupa, la imagen que ves a través de ella es más grande. El centro de homotecia está aproximadamente en el centro de la lupa. El factor de homotecia depende de la distancia entre el objeto y la lupa, y también de la distancia entre la lupa y tu ojo.

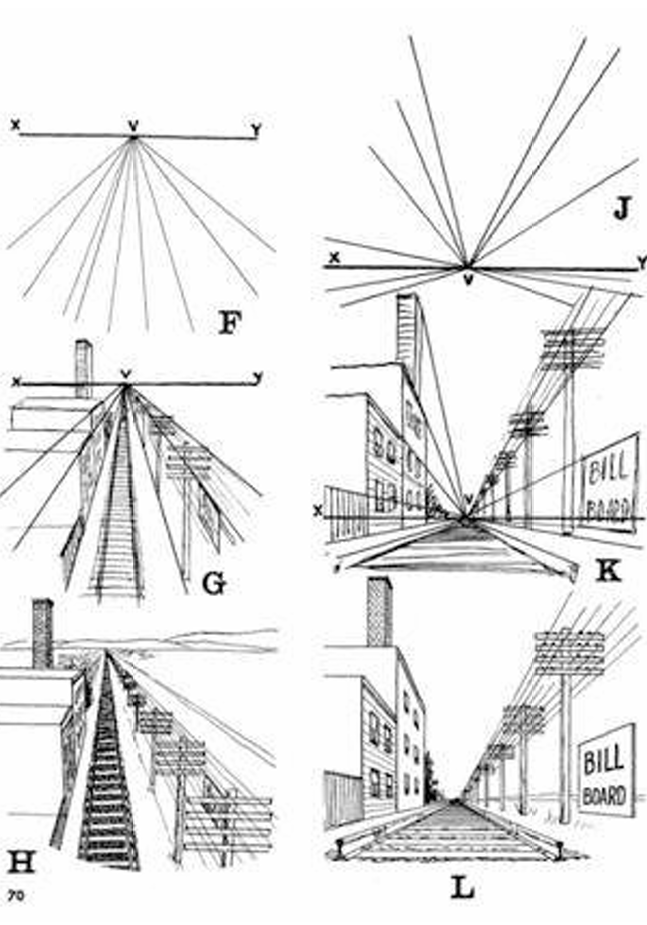
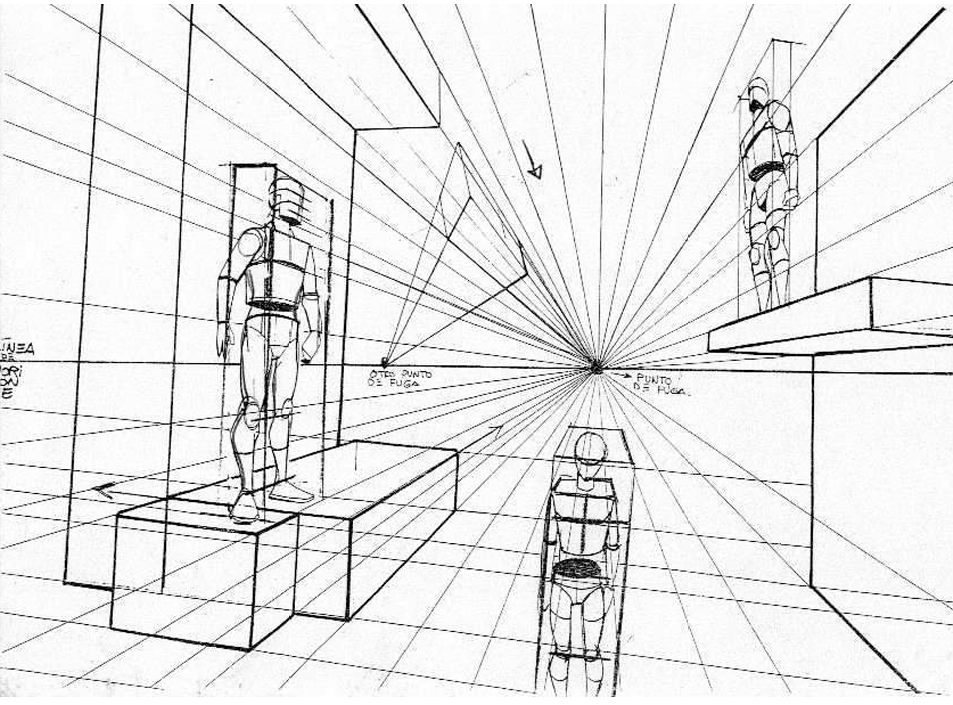
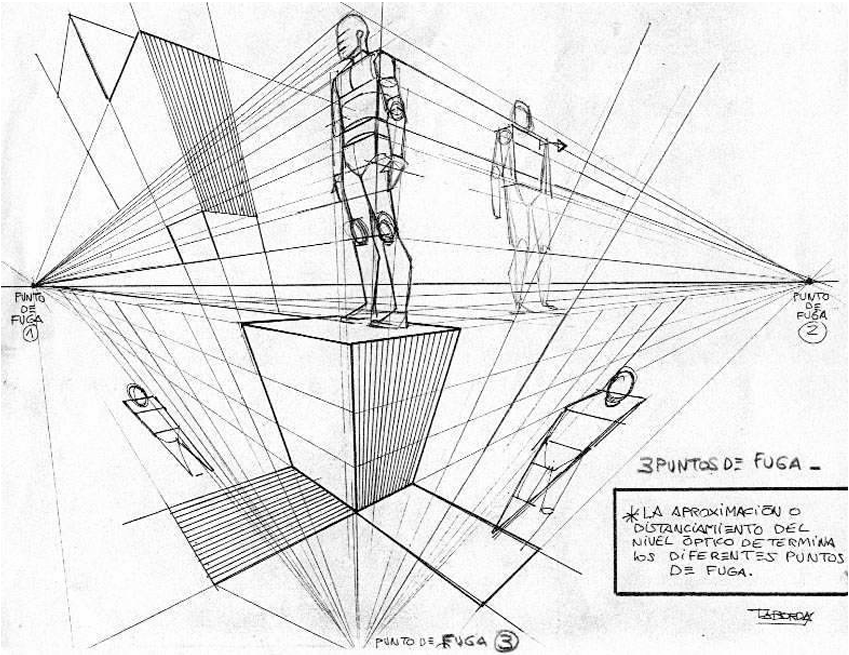
Ejemplo 2: Perspectiva en un dibujo (Convergencia en un punto)

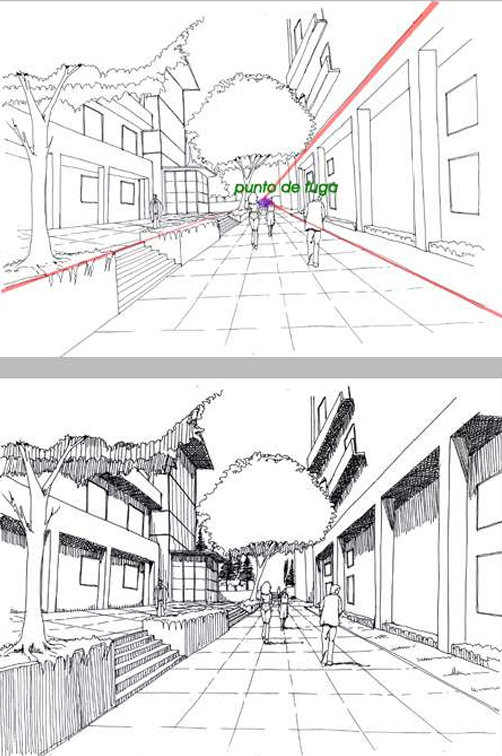
En un dibujo en perspectiva, las líneas paralelas (como los bordes de un camino o de un edificio) parecen converger en un punto lejano llamado *punto de fuga*. Este punto de fuga puede interpretarse como el "centro" de una especie de homotecia. Aunque la perspectiva no es *exactamente* una homotecia en el sentido matemático estricto (porque las distancias no se escalan de manera perfectamente uniforme), la idea básica de "proyección desde un punto" está presente.

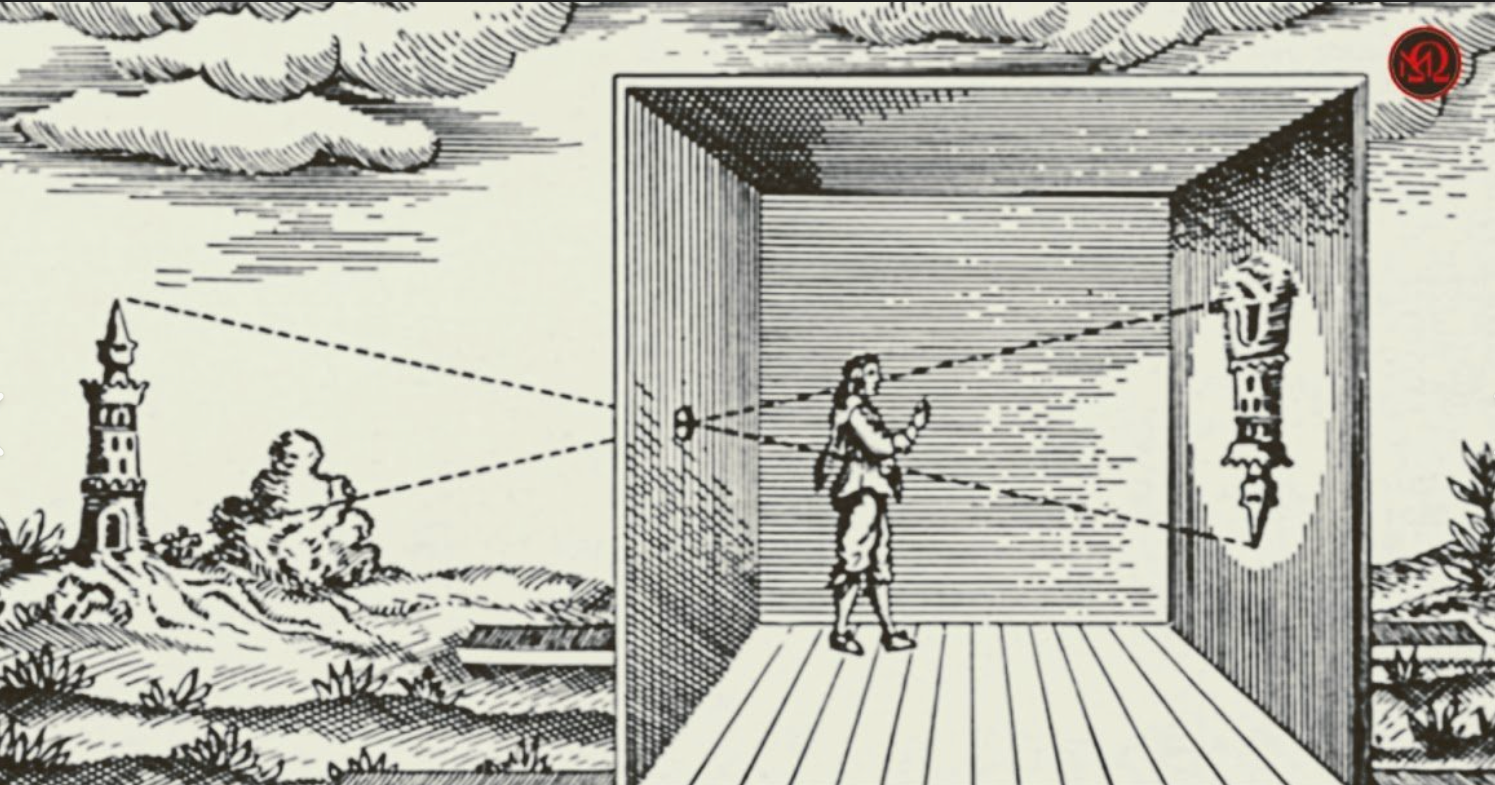
Ejemplo 3. Cámara oscura (Inversión y reducción)

Una caja con un pequeño agujero en uno de sus lados. La luz que entra por ese orificio proyecta una imagen invertida de la escena exterior en la pared opuesta de la caja. El agujero funciona como el centro de la homotecia, la imagen es reducida (|k| < 1) e invertida (k < 0).

Práctica

Ahora, ¡a practicar! Aquí tienes 10 ejercicios (3 conceptuales y 7 prácticos) y 4 problemas para aplicar lo que has aprendido.

Ejercicios

1. (Conceptual) Explica, con tus propias palabras, por qué la imagen que se forma en la retina de tu ojo se puede considerar como el resultado de una homotecia. ¿Cuál es el centro de homotecia en este caso? ¿Qué puedes decir sobre el factor de homotecia?

   Solución: Los rayos de luz que provienen de un objeto entran en el ojo y son enfocados por el cristalino (que actúa como una lente convergente). Estos rayos convergen en la retina, formando una imagen. El cristalino actúa como el centro de homotecia. La imagen en la retina es más *pequeña* que el objeto real (por lo que \(0 < |k| < 1\)) y está *invertida* (por lo que \(k\) es negativo).

2. (Conceptual) Cuando proyectas la sombra de un objeto usando una linterna, ¿qué representa la linterna en términos de homotecia?

   Solución: La linterna (más precisamente, la fuente de luz dentro de la linterna) actúa como el centro de homotecia. Los rayos de luz emanan de este punto, "golpean" el objeto y proyectan su sombra en la superficie (pared, suelo, etc.).

3. (Conceptual) ¿Por qué las líneas paralelas en el mundo real pueden seguir viéndose paralelas en algunas imágenes, mientras que en otras parecen converger en un punto de fuga, como ocurre en fotografías, proyecciones o la visión humana?

   Solución: La percepción del paralelismo en una imagen depende del tipo de proyección utilizada. En una proyección ortogonal (como en planos técnicos o ciertos gráficos), las líneas paralelas en la realidad siguen siendo paralelas en la imagen. Esto ocurre porque los rayos de luz o las líneas de proyección son perpendiculares al plano de la imagen, lo que evita la convergencia. Sin embargo, en una proyección en perspectiva, como la que realiza una cámara o el ojo humano, las líneas paralelas parecen converger en un punto de fuga. Esto sucede porque los rayos de luz que provienen de objetos distantes entran al ojo o a la cámara desde un mismo punto de observación, generando el efecto de profundidad. Aunque en la realidad las líneas siguen siendo paralelas, la imagen proyectada en la retina o en un sensor digital las muestra convergiendo, lo que da la ilusión de tridimensionalidad. Este fenómeno explica por qué, por ejemplo, las vías del tren parecen juntarse en el horizonte, aunque sabemos que en la realidad son siempre paralelas.

4. (Práctica) Describe un experimento sencillo que podrías hacer en casa para demostrar cómo cambia el tamaño de una sombra al modificar la distancia entre el objeto y la fuente de luz (por ejemplo, una lámpara).

   Solución: Necesitas una lámpara de escritorio (o una linterna) y un objeto pequeño (como un lápiz, una figura de juguete, etc.).

   1. Coloca la lámpara en un extremo de una mesa y una pared (o una hoja grande de papel) en el otro extremo.
   2. Apaga las otras luces de la habitación para que la sombra sea más nítida.
   3. Sostén el objeto entre la lámpara y la pared.
   4. Acerca el objeto a la lámpara. Observa cómo la sombra se hace *más grande*.
   5. Aleja el objeto de la lámpara (acercándolo a la pared). Observa cómo la sombra se hace *más pequeña*.

   Esto demuestra que el factor de homotecia (y, por lo tanto, el tamaño de la sombra) depende de la distancia entre la fuente de luz y el objeto.

5. (Práctica) Si tienes un proyector de diapositivas (o un proyector digital), ¿qué parte del proyector actúa como el centro de homotecia?

   Solución: La fuente de luz dentro del proyector (la lámpara o el LED) actúa como el centro de homotecia. La imagen pequeña en la diapositiva (o en el chip digital) se amplía y se proyecta en la pantalla.

6. (Práctica) ¿Por qué la imagen que ves a través de una lupa cambia de tamaño dependiendo de qué tan cerca o lejos esté el objeto de la lupa? Explícalo en términos de homotecia.

   Solución: La lupa es el centro de homotecia. El factor de homotecia depende de la distancia entre el objeto y la lupa, y también de la distancia entre la lupa y tu ojo. Al cambiar estas distancias, cambias el factor de homotecia y, por lo tanto, el tamaño de la imagen que ves.

7. (Práctica) Da un ejemplo de la vida diaria donde la homotecia resulte en una *reducción* del tamaño, en lugar de una ampliación.

   Solución: Una cámara fotográfica es un excelente ejemplo. La lente de la cámara toma una escena grande del mundo real y la reduce a una imagen pequeña que cabe en el sensor (o en la película, en las cámaras antiguas). El ojo humano funciona de la misma manera, reduciendo la imagen del mundo exterior a la retina.

8. (Práctica) Quieres que la sombra de un objeto sea el doble de grande que el objeto mismo. ¿Cómo deberías colocar el objeto, la fuente de luz y la superficie donde se proyecta la sombra? (No necesitas dar medidas exactas, solo describe la relación entre las distancias).

   Solución: Para que la sombra sea el doble de grande que el objeto, la distancia entre la fuente de luz y la superficie de proyección (por ejemplo, la pared) debe ser el *doble* de la distancia entre la fuente de luz y el objeto. Es decir la distancia entre el objeto y la pared/superficie debe ser igual a la distancia entre la fuente de luz y el objeto.

9. (Práctica) ¿En qué se diferencian las sombras que produce el sol (en un día soleado) de las sombras que produce una linterna en una habitación oscura? Relaciona tu respuesta con la idea de homotecia.

   Solución:

   • Sombras del sol: El sol está tan lejos de la Tierra que sus rayos llegan a nosotros prácticamente *paralelos*. Esto significa que la sombra de un objeto tiene casi el mismo tamaño y forma que el objeto mismo (no hay una ampliación o reducción significativa). No hay un centro de homotecia cercano y definido.
   • Sombras de una linterna: La linterna es una fuente de luz *puntual* y *cercana*. Los rayos de luz divergen desde la linterna, creando una homotecia con la linterna como centro. El tamaño de la sombra depende mucho de las distancias entre la linterna, el objeto y la superficie donde se proyecta la sombra.
10. (Práctica) En una camara fotografica, ¿Que elemento define el factor de homotecia?

    Solución: El factor de reducción, en este caso, está determinado principalmente por la distancia focal de la lente (objetivo) de la cámara y la distancia entre la lente y el sensor (o película).

Problemas

1. Un proyector está a 2 metros de una pared, y la imagen proyectada en la pared mide 1 metro de ancho. Si queremos que la imagen proyectada mida 2 metros de ancho, ¿a qué distancia de la pared deberíamos colocar el proyector? (Asume que la relación entre la distancia y el tamaño de la imagen es lineal).

   Solución: Si queremos *duplicar* el tamaño de la imagen, necesitamos *duplicar* la distancia entre el proyector y la pared. Por lo tanto, deberíamos colocar el proyector a 4 metros de la pared.

2. Observa tu propia sombra en el suelo en un día soleado. Luego, en una habitación oscura, usa una linterna para proyectar la sombra de tu mano sobre una pared. Compara y contrasta las dos situaciones. ¿En qué se parecen y en qué se diferencian las sombras? ¿Cómo se relaciona esto con la homotecia?

   Solución:

   • Sombra del sol: Tu sombra en el suelo en un día soleado tendrá aproximadamente tu mismo tamaño y forma. Los rayos del sol son casi paralelos, por lo que no hay una ampliación o reducción significativa.
   • Sombra de la linterna: La sombra de tu mano proyectada por la linterna será mucho más grande que tu mano, y su tamaño cambiará drásticamente si mueves tu mano o la linterna. La linterna es una fuente de luz puntual que actúa como centro de homotecia.

   La principal diferencia es que, en el caso del sol, no hay un centro de homotecia cercano y definido, mientras que en el caso de la linterna, sí lo hay (la propia linterna).

3. Imagina que quieres diseñar un experimento sencillo para que los estudiantes puedan comprobar, de forma visual y práctica, que una lupa produce una homotecia con un factor de ampliación mayor que 1 (\(|k| > 1\)). Describe los materiales que necesitarías y los pasos que seguirían los estudiantes.

   Solución:

   Materiales:

   • Una lupa
   • Una regla (con marcas de milímetros bien visibles)
   • Una hoja de papel con un texto impreso pequeño (o una cuadrícula dibujada)

   Pasos:

   1. Coloca la hoja de papel con el texto (o la cuadrícula) sobre una mesa.
   2. Sostén la lupa a una cierta distancia por encima de la hoja.
   3. Mira a través de la lupa el texto (o la cuadrícula).
   4. Observa que las letras (o los cuadrados de la cuadrícula) se ven más grandes a través de la lupa que a simple vista.
   5. Usa la regla para medir *aproximadamente* el tamaño de una letra (o de un cuadrado de la cuadrícula) *sin* la lupa, y luego mide el tamaño de la *misma* letra (o cuadrado) *a través* de la lupa. (Las medidas no serán perfectas, pero servirán para tener una idea de la ampliación).
   6. Compara las dos medidas. La medida a través de la lupa debería ser mayor que la medida sin la lupa. Esto demuestra que la lupa está produciendo una ampliación (\(|k| > 1\)).
   7. (Opcional) Varía la distancia entre la lupa y la hoja, y observa cómo cambia el tamaño de la imagen.
4. Una cámara oscura es una caja cerrada con un pequeño orificio en una de sus caras. La luz que entra por el orificio proyecta una imagen invertida de la escena exterior en la cara opuesta de la caja. Explica cómo funciona la cámara oscura utilizando el concepto de homotecia. ¿Cuál es el centro de homotecia? ¿Qué puedes decir sobre el factor de homotecia?

   Solución: La cámara oscura es un ejemplo clásico de homotecia.

   • Centro de homotecia: El pequeño orificio por donde entra la luz actúa como el centro de homotecia.
   • Factor de homotecia: La imagen que se forma en la pared opuesta de la caja es una versión *reducida* de la escena exterior (por lo que \(0 < |k| < 1\)). Además, la imagen está *invertida* (por lo que \(k\) es negativo).

   Los rayos de luz viajan en línea recta desde los objetos de la escena exterior, pasan por el orificio (centro de homotecia) y se proyectan en la pared opuesta, formando la imagen invertida y reducida.

Homotecia - Página 3: Construcción y Modelos Concretos

Introducción

En esta página, vamos a aprender a construir homotecias a mano, usando regla y compás. También veremos cómo algunos objetos y experimentos de la vida real, como la proyección de sombras, nos pueden ayudar a entender mejor este concepto. ¡Manos a la obra!

Modelos Concretos de Homotecia

Hay varios experimentos y objetos que nos ayudan a visualizar la homotecia, si todavia no logras comprender este fenomeno te invito a realizar alguno de estos experimentos:

• Proyección de sombras: Una lámpara o linterna actúa como el centro de homotecia. Un objeto (como un lápiz o un bloque) se coloca entre la lámpara y una pared (la "pantalla"). La sombra que se proyecta en la pared es una figura homotética del objeto. Si acercas el objeto a la lámpara, la sombra se agranda (el factor de homotecia aumenta). Si alejas el objeto de la lámpara, la sombra se reduce.
• Varillas y bloques (o cartón): Puedes usar varillas delgadas (como palillos de brocheta) para representar los "rayos" que salen del centro de homotecia (una linterna o un punto marcado en un papel). Coloca un bloque (o un trozo de cartón con una forma recortada) entre la fuente de luz y una superficie. Las varillas te ayudarán a visualizar cómo se proyectan los vértices del objeto y cómo se forma la sombra homotética.
• Cámara oscura: Una caja con un pequeño agujero. La luz entra por el orificio, y la imagen del exterior, invertida, se proyecta en la pared contraria.

Construcción Manual de una Homotecia (con Regla y Compás)

Para construir la imagen de una figura \(F\) después de aplicarle una homotecia con centro \(O\) y factor \(k\), sigue estos pasos:

1. Elige un punto como centro \(O\). Puede estar dentro, fuera o sobre la figura.
2. Traza líneas rectas. Desde el centro \(O\), traza una línea recta que pase por cada uno de los vértices (esquinas) de la figura \(F\). Estas líneas son como "rayos" que salen de \(O\).
3. Mide y multiplica. Para cada vértice \(P\) de la figura original:
   • Mide la distancia entre el centro \(O\) y el vértice \(P\) (la distancia \(OP\)).
   • Multiplica esa distancia por el valor absoluto de \(k\) (\(|k|\)). Esto te dará la distancia a la que estará el nuevo punto \(P'\).
   • ¿Dónde colocar \(P'\)?
     • Si \(k\) es positivo, el nuevo punto \(P'\) estará en la *misma dirección* que \(P\) respecto a \(O\), sobre la línea que ya dibujaste.
     • Si \(k\) es negativo, el nuevo punto \(P'\) estará en la *dirección opuesta* a \(P\) respecto a \(O\). Es decir, estará al otro lado de \(O\), pero sobre la misma línea.
   • Marca el nuevo punto \(P'\) a la distancia calculada.
4. Repite. Haz lo mismo con todos los demás vértices de la figura original.
5. Une los puntos. Une los nuevos puntos (\(P'\), etc.) en el mismo orden en que estaban unidos los puntos originales. Así obtendrás la figura transformada \(F'\).

Consejo: Si usas un compás, puedes medir la distancia \(OP\) y luego "transportarla" a lo largo de la línea la cantidad de veces que indique \(|k|\). Si \(k\) es una fracción, como \(\frac{1}{2}\), divide la distancia \(OP\) en el número de partes que indica el denominador (en este caso, 2) y toma la cantidad de partes que indica el numerador (en este caso, 1).

Ejemplos

Ejemplo de Construcción:

Queremos construir la imagen de un triángulo \(ABC\) después de aplicarle una homotecia con centro \(O\) (un punto fuera del triángulo) y factor \(k = 1.5\).

1. Dibujamos el triángulo \(ABC\) y el punto \(O\).
2. Dibujamos líneas rectas desde \(O\) hasta cada uno de los vértices \(A\), \(B\) y \(C\).
3. Medimos la distancia \(OA\). La multiplicamos por 1.5. Marcamos el punto \(A'\) sobre la línea \(OA\), a esa nueva distancia de \(O\).
4. Repetimos el paso 3 para los puntos \(B\) y \(C\), obteniendo \(B'\) y \(C'\).
5. Unimos los puntos \(A'\), \(B'\) y \(C'\) para formar el triángulo \(A'B'C'\), que es la imagen homotética de \(ABC\).

Práctica

¡A practicar!

Ejercicios Prácticos de Homotecia

Instrucciones: Utiliza regla y compás para realizar las construcciones. Describe los pasos y la figura resultante.

Ejercicios

1. Triángulo simple, *k* > 1:

   Dibuja un triángulo ABC con vértices en A, B y C. Elige un punto O fuera del triángulo. Construye la imagen homotética del triángulo ABC con centro O y factor de homotecia k = 2. Describe detalladamente los pasos, y describe como es la figura resultante en relacion a la original.

   Solución (Pasos detallados):

   1. Dibujo el triángulo ABC y elijo un punto O fuera de él.
   2. Trazo una línea recta desde O hasta el vértice A.
   3. Con el compás, tomo la distancia OA.
   4. Manteniendo la abertura del compás, coloco la punta metálica en A y trazo un arco que corte la prolongación de la línea OA . El punto de intersección es A', que está a una distancia 2 * OA de O.
   5. Repito los pasos 2, 3 y 4 para los vértices B y C, obteniendo los puntos B' y C'.
   6. Uno los puntos A', B' y C' en el mismo orden en que estaban unidos los vértices originales (A, B, C). Así obtengo el cuadrilátero A'B'C', que es la imagen homotética de ABC.

   La figura resultante A'B'C' es un triangulo, con la misma forma que el triangulo original, sus lados paralelos correspondientes son paralelos, y cada lado del nuevo triangulo mide el doble que el lado correspondiente del triangulo original. Ademas A'B'C' se encuentra en la misma direccion con respecto al centro O que el triangulo original.

2. Cuadrilátero, *k* < -1:

   Dibuja un cuadrilátero irregular ABCD. Elige un punto O fuera del cuadrilátero. Construye la imagen homotética de ABCD con centro O y factor k = -1.5. Describe como es la figura resultante en relacion a la original

   Solución (Pasos):

   1. Dibujo el cuadrilatero ABCD y elijo un punto O fuera de él.
   2. Trazo una línea recta desde O hasta el punto A.
   3. Mido la distancia OA.
   4. Multiplico esa distancia por 1.5 (porque |k| = 1.5).
   5. Como k es negativo, marco el punto A' a la distancia 1.5 * OA de O, pero en el lado opuesto de O respecto a A, sobre la línea que ya tracé.
   6. Repito los pasos 2, 3, 4 y 5 para el punto B, C y D obteniendo el punto B',C' y D'.
   7. Uno los puntos A' , B', C' y D' para obtener el cuadrilatero A'B'C'D', que es la imagen homotética de ABCD.

   La figura resultante es un cuadrilatero con la misma forma que ABCD, sus lados correspondientes son paralelos y, ademas sus lados miden 1.5 veces el tamaño de los lados del cuadrilatero original. Con respecto a la ubicacion relativa al centro de homotecia, la figura resultante esta al otro lado del centro de homotecia O.

3. Triángulo, 0 < *k* < 1:

   Dibuja un triángulo PQR. Elige un punto O dentro del triángulo. Construye la imagen homotética de PQR con centro O y factor k = 1/2. Describe como es la figura resultante en relacion a la original.

   Solución (Pasos):

   1. Dibujo el triángulo PQR y elijo un punto O *dentro* del triángulo.
   2. Trazo líneas rectas desde O hasta cada uno de los vértices P, Q y R.
   3. Para cada vértice X:
      • Mido la distancia OX con la regla.
      • Divido esa distancia entre 2 (porque k = 1/2).
      • Marco un punto X' sobre la línea OX, a la distancia OX/2 de O. Como O está dentro del triángulo, X' también estará dentro del triángulo, más cerca de O que de X.
   4. Uno los puntos P', Q' y R' para formar el triángulo P'Q'R', que es la imagen homotética de PQR.

   El triangulo resultante es semejante al original, es decir, sus angulos correspondientes son iguales y sus lados correspondientes son proporcionales (paralelos) , en este caso cada lado del nuevo triangulo mide la mitad del original. Con respecto al centro de homotecia, ambos se encuentra del mismo lado, y la imagen homotetica se encuentra al interior del triangulo original.

4. Pentágono, *k* = 1 (Caso especial):

   Dibuja un pentágono irregular ABCDE. Elige un punto O cualquiera. Construye la imagen homotética con centro O y factor k = 1. ¿Qué observas?

   Solución:

   Si sigues los pasos de la construcción, notarás que cada punto imagen P' coincide exactamente con el punto original P. Esto se debe a que multiplicar cualquier distancia por 1 da como resultado la misma distancia. La figura homotética es *idéntica* a la original y está *superpuesta* a ella.

   Observacion: Al aplicar una homotecia con k=1 la figura resultante es congruente con la original, y se encuentra superpuesta.

5. Segmento, *k* negativo, centro en el segmento:

   Dibuja un segmento de recta AB. Elige un punto O que esté sobre el segmento AB (entre A y B). Construye la imagen homotética del segmento AB con centro O y factor k = -2. Describe como es la figura resultante en relacion a la original.

   Solución (Pasos):

   1. Dibujo el segmento AB y elijo un punto O sobre él.
   2. Trazo una línea recta que contiene al segmento desde O hasta el punto A. Como O esta sobre AB, extiendo la recta.
   3. Mido la distancia OA.
   4. Multiplico esa distancia por 2 (porque |k| = 2).
   5. Como k es negativo, marco el punto A' a la distancia 2 * OA de O, pero en el lado opuesto de O respecto a A, sobre la línea que ya tracé.
   6. Repito los pasos 2, 3, 4 y 5 para el punto B, obteniendo el punto B'.
   7. El segmento A'B', es la imagen homotética de AB.

   La figura resultante es un segmento, colineal con el segmento original, pero de tamaño doble. Ademas, el punto O divide tambien al segmento resultante A'B' de la misma forma que divide al segmento AB.

6. Triangulo Rectangulo con k fraccionario

   Dibuja un triangulo rectangulo ABC, donde A es el vertice del angulo recto. Elije un punto O fuera del triangulo. Construye la imagen homotetica de ABC con centro O y factor k=2/3. Describe como es la figura resultante en relacion a la original.

   Solución (Pasos):

   1. Dibujo el triangulo ABC y elijo un punto O fuera de él.
   2. Trazo una línea recta desde O hasta el vértice A.
   3. Con el compás, tomo la distancia OA.
   4. Manteniendo la abertura del compás, coloco la punta metálica en O y trazo un arco que corte la prolongación de la línea OA . El punto de intersección lo llamaremos P.
   5. Manteniendo la abertura del compás, coloco la punta metálica en P y trazo un arco que corte la prolongación de la línea OA . El punto de intersección lo llamaremos Q.
   6. Ahora, con el compas tomo la distancia de O hasta Q. Con esta abertura, corto la linea OA desde el punto O, obteniendo el punto A'.
   7. Repito los pasos 2 a 6 para los vertices B y C
   8. Uno los puntos A',B' y C'.

   La figura resultante es un triangulo rectangulo, donde el vertice del angulo recto es A'. Sus lados son paralelos a los del triangulo original, y cada lado mide 2/3 del lado correspondiente del triangulo original.

Problemas

1. Determinación del Centro (Triángulo):

   Imagen: Dos triángulos, ABC y A'B'C', que son homotéticos. Las líneas AA', BB' y CC' deben ser claramente *no* paralelas, y deben concurrir en un punto O (que el estudiante debe encontrar). Los triángulos no deben ser congruentes.

   Se te dan dos triángulos, ABC y A'B'C', que se sabe que son homotéticos. Describe detalladamente cómo encontrarías el centro de homotecia O usando solo regla y compás. Además, explica cómo determinarías si el factor de homotecia k es positivo o negativo, y cómo estimarías su valor (sin necesidad de una medición precisa, solo una estimación razonable).

   Solución:

   Encontrar el centro de homotecia (O):

   1. Traza una línea recta que conecte un par de puntos correspondientes, por ejemplo, A y A'.
   2. Traza otra línea recta que conecte otro par de puntos correspondientes, por ejemplo, B y B'.
   3. El punto donde se intersecan estas dos líneas es el centro de homotecia, O.
   4. (Verificación) Traza la línea que conecta C y C'. Esta línea *debe* pasar también por O. Si no pasa por O, hay un error en la construcción o las figuras no son realmente homotéticas.

   Determinar el signo y estimar el valor de k:

   • Signo: Si A y A' están del *mismo lado* de O, entonces k es positivo. Si están en *lados opuestos* de O, entonces k es negativo.
   • Valor (estimación):
     • Si k es positivo: Compara visualmente la longitud de OA' con la longitud de OA. Si OA' parece ser el doble de largo que OA, entonces k es aproximadamente 2. Si OA' parece ser la mitad de OA, entonces k es aproximadamente 1/2. Usa esta comparación visual para estimar k.
     • Si k es negativo: Haz lo mismo que en el caso positivo, pero compara las *magnitudes* de las distancias (ignorando la dirección). El valor de k será el negativo de tu estimación. Por ejemplo, si OA' parece ser tres veces OA, pero en dirección opuesta, entonces k es aproximadamente -3.
2. Determinación del Centro (Cuadrilátero, *k* negativo):

   Imagen: Dos cuadriláteros, ABCD y A'B'C'D', homotéticos. El centro O debe estar *entre* las dos figuras. Las líneas AA', BB', CC' y DD' deben concurrir en O.

   Se te dan dos cuadriláteros, ABCD y A'B'C'D', que son homotéticos, y se sabe que el factor de homotecia k es negativo. Describe cómo encontrarías el centro de homotecia O usando regla y compás.

   Solución:

   El procedimiento es el mismo que en el problema anterior, a pesar de que k sea negativo. La clave es que las líneas que conectan puntos correspondientes *siempre* concurren en el centro de homotecia, sin importar el signo de k.

   1. Traza una línea recta que conecte un par de puntos correspondientes, por ejemplo, A y A'.
   2. Traza otra línea recta que conecte otro par de puntos correspondientes, por ejemplo, B y B'.
   3. El punto donde se intersecan estas dos líneas es el centro de homotecia, O.
   4. (Verificación) Traza las lineas que unen los vertices correspondientes restantes. Todas deben pasar por O.

   Como k es negativo, el centro O estará *entre* las dos figuras.

3. Construccion y descripcion

   Dibuja un hexagono irregular ABCDEF. Elije un punto O dentro del hexagono. Realiza 3 homotecias con centro en O, con factores k=1/3, k=1 y k=-2. Describe cada figura resultante en relacion a la original.

   Solución:

   Se debe aplicar el procedimiento de homotecia a cada vertice del hexagono, para cada uno de los factores k dados.

   k = 1/3:

   • La figura resultante será un hexágono semejante al original (mismos ángulos, lados proporcionales).
   • Cada lado del nuevo hexágono medirá 1/3 del lado correspondiente del hexágono original.
   • El nuevo hexágono estará ubicado entre el centro O y el hexágono original.
   • Todos los puntos correspondientes (vértices y cualquier punto dentro del hexágono) estarán alineados con el centro O.

   k = 1:

   • La figura resultante es identica al hexagono original, superpuesta a él.

   k = -2:

   • La figura resultante será un hexágono semejante al original.
   • Cada lado del nuevo hexágono medirá el doble del lado correspondiente del hexágono original.
   • El nuevo hexágono estará ubicado al otro lado del centro O, con respecto al hexágono original. Estará "invertido" con respecto a O.
   • Todos los puntos correspondientes estarán alineados con el centro O, pero en direcciones opuestas desde O.