semejanzas y escalas
| Sitio: | PROFEARAUCO.CL |
| Curso: | Media 1 |
| Libro: | semejanzas y escalas |
| Imprimido por: | Invitado |
| Día: | domingo, 8 de marzo de 2026, 02:58 |
1. Diferencia geométrica entre congruencia, equivalencia y semejanza
Preguntas y Respuestas - Semejanza y CongruenciaDiferencia geométrica entre congruencia, equivalencia y semejanza
En geometría, es fundamental comprender las relaciones entre las figuras. Aquí te presento las diferencias entre tres conceptos clave:
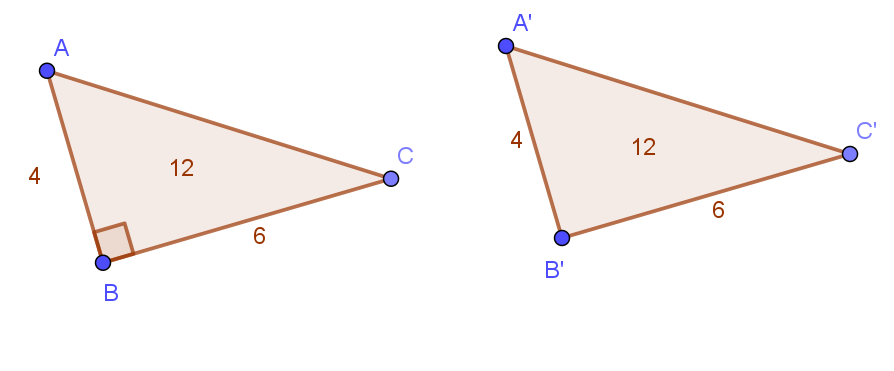
Congruencia
Dos figuras son congruentes si tienen la misma forma y tamaño. Imagina dos monedas idénticas: son congruentes.
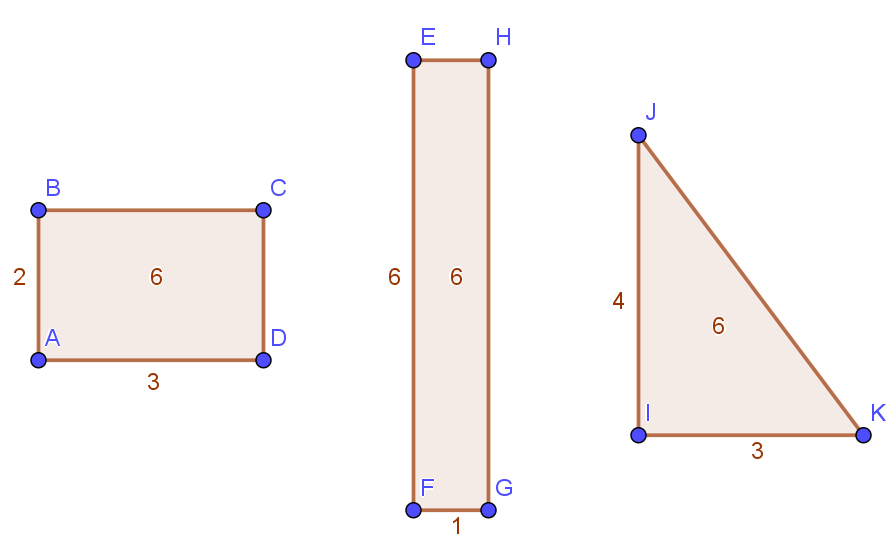
Equivalencia
Dos figuras son equivalentes si tienen la misma área, pero no necesariamente la misma forma. Un triángulo y un rectángulo pueden ser equivalentes si ambos encierran la misma superficie.
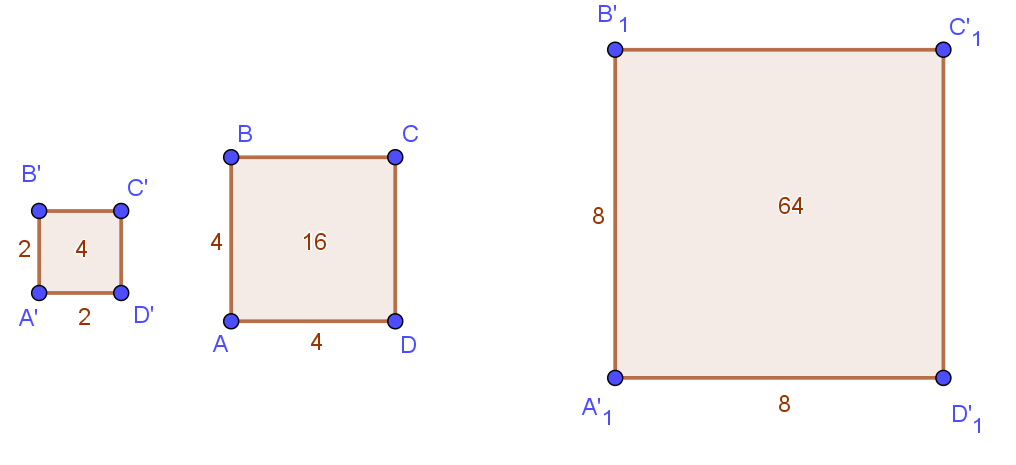
Semejanza
Dos figuras son semejantes si tienen la misma forma, pero pueden tener diferente tamaño. Una fotografía y su versión en miniatura son semejantes.
En resumen:
- Congruencia: Igual forma y tamaño.
- Equivalencia: Igual área (misma superficie), forma puede variar.
- Semejanza: Igual forma, tamaño puede variar (escalado).
Explorando la congruencia, semejanza y equivalencia de figuras
En la siguiente actividad, interactuarás con un applet de GeoGebra donde podrás visualizar cómo se relacionan las figuras bajo diferentes transformaciones geométricas. Al mover los puntos en las figuras, observarás cómo cambian las longitudes y posiciones de los lados, y cómo las líneas que unen los vértices correspondientes se comportan en los casos de congruencia, semejanza y equivalencia.
1. ¿Cómo son las líneas que unen los vértices correspondientes en figuras congruentes?
2. ¿En qué se parecen y en qué se diferencian las figuras congruentes y las figuras semejantes?
3. En el caso de figuras equivalentes, ¿qué sucede si modifico la medida de uno de sus lados?
4. ¿Es posible que dos figuras sean semejantes pero no equivalentes? ¿Y al revés? Explica con ejemplos.
5. Si una figura es semejante a otra, ¿cómo se relacionan sus perímetros y áreas?
6. Si dos figuras son semejantes, ¿podrían ser también congruentes? Explica en qué condiciones sucede esto.
7. En figuras equivalentes, ¿qué propiedades geométricas se conservan y cuáles cambian?
8. ¿Es correcto afirmar que una figura congruente es una combinación de semejanza y equivalencia? Justifica tu respuesta.
2. Semejanza de Figuras Geométricas
Semejanza de Figuras Geométricas
Definición:
Recordemos que dos figuras geométricas son semejantes si tienen la misma forma, pero no necesariamente el mismo tamaño. Una figura puede ser una versión a escala de la otra (más grande o más pequeña). La congruencia es un caso especial de semejanza, donde la razón de semejanza es exactamente 1. Es decir, dos figuras congruentes son semejantes, pero dos figuras semejantes no son necesariamente congruentes.
Características Clave de Figuras Semejantes:
Semejanza de Polígonos:
Para que dos polígonos sean semejantes, deben cumplirse todas las siguientes condiciones:
- Mismo Número de Lados: Deben tener la misma cantidad de lados.
- Ángulos Correspondientes Congruentes: Todos los pares de ángulos correspondientes deben medir lo mismo.
- Lados Correspondientes Proporcionales: La razón entre las longitudes de los lados correspondientes debe ser la misma para todos los pares de lados.
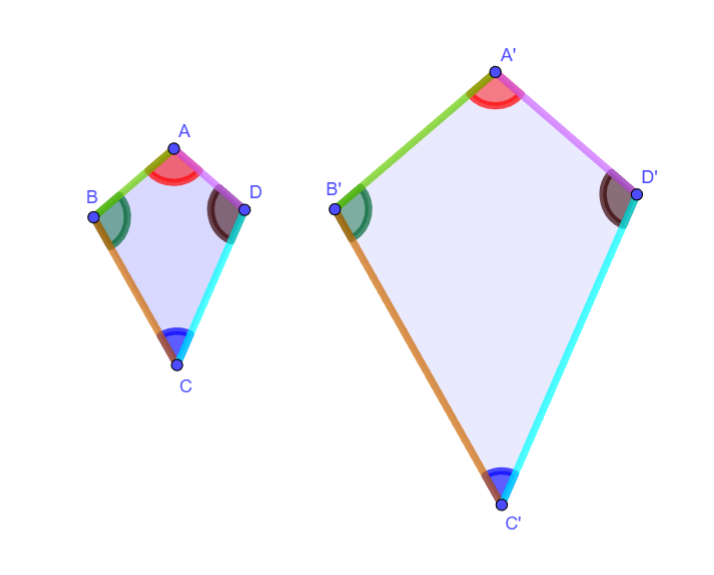
Ejemplo y contraejemplo:
- Todos los cuadrados son semejantes entre sí. Siempre tienen ángulos de 90 grados, y la razón de semejanza es simplemente la proporción entre las longitudes de sus lados.
- Un rectángulo y un cuadrado no son semejantes en general, a menos que el rectángulo también sea un cuadrado. Aunque pueden tener ángulos correspondientes iguales (todos rectos), sus lados no serán proporcionales a menos que sea un caso especial.
Semejanza de Triángulos (Caso Especial Importante):
Los triángulos son un caso especial, y existen criterios específicos que simplifican la determinación de la semejanza. No es necesario verificar todas las condiciones; basta con cumplir uno de estos criterios:
-
Criterio Ángulo-Ángulo (AA): Si dos triángulos tienen dos ángulos correspondientes congruentes, entonces son semejantes. (Si dos ángulos son iguales, el tercero también lo es).
-
Criterio Lado-Lado-Lado (LLL): Si los tres lados de un triángulo son proporcionales a los tres lados correspondientes de otro triángulo, entonces son semejantes.
-
Criterio Lado-Ángulo-Lado (LAL): Si dos triángulos tienen un ángulo correspondiente congruente, y los lados que forman ese ángulo son proporcionales, entonces son semejantes.
Una Definición Alternativa de Semejanza de Polígonos:
Dos polígonos son semejantes si se pueden descomponer en el mismo número de triángulos semejantes, dispuestos de la misma manera. Es decir, si podemos trazar diagonales en ambos polígonos de tal forma que obtengamos triángulos, y cada triángulo en un polígono es semejante a su triángulo correspondiente en el otro polígono.
Por ejemplo si deseamos saber si el siguiente par de poligonos son semejantes....
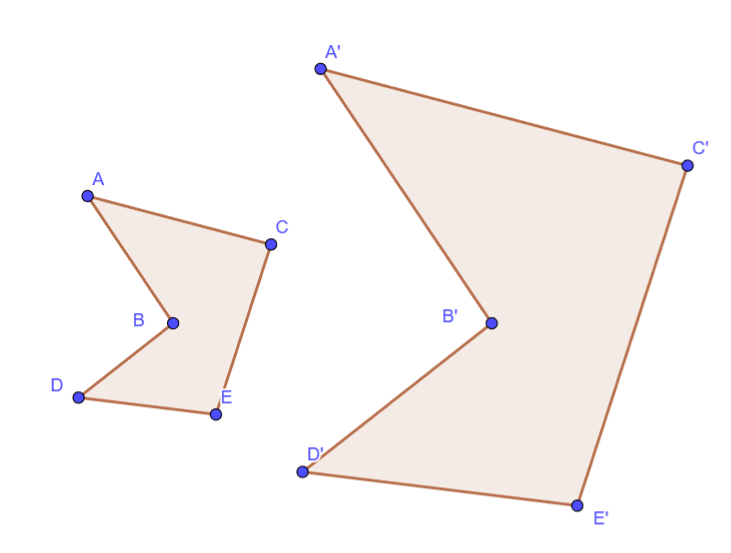
podemos estudiar si los triangulos que respectivamente lo componen son semejantes y estan puestos en el mismo orden.
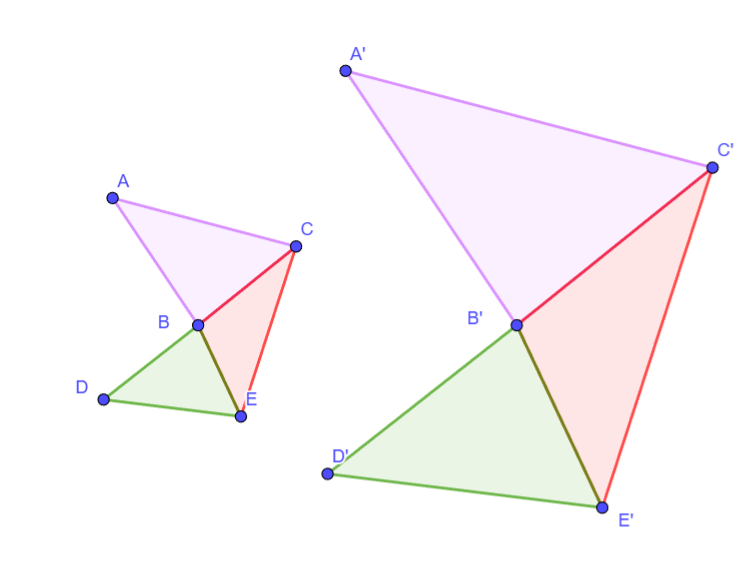
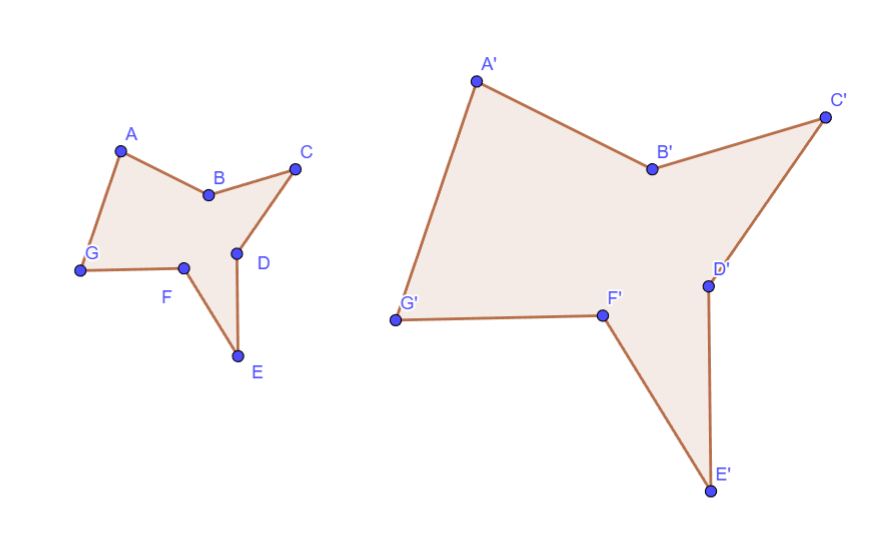
Semejanza de Figuras Irregulares (Planas):
Dos figuras planas irregulares son semejantes si una es una versión a escala de la otra. Como en estas figuras no siempre tenemos ángulos definidos para comparar, la condición de semejanza se basa en la proporcionalidad de las distancias. Para cualquier par de puntos correspondientes en las dos figuras, la razón entre sus distancias debe ser constante e igual a la razón de semejanza. Esta condición generaliza la idea de lados proporcionales en polígonos. Es necesario establecer una correspondencia clara entre los puntos de ambas figuras. Visualmente, deben tener la "misma forma", pero una puede ser más grande o más pequeña. Es importante destacar que todas las distancias correspondientes deben mantener la misma proporción para que la semejanza se cumpla.
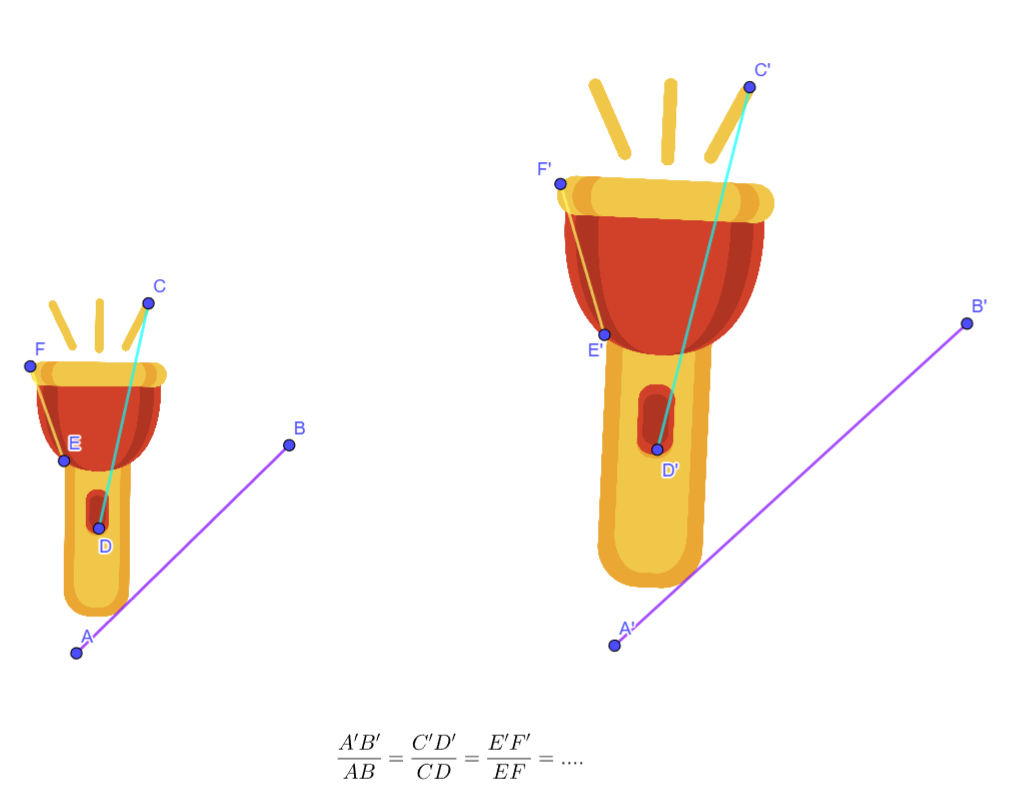
Aplicaciones:
La semejanza tiene numerosas aplicaciones prácticas, incluyendo:
- Cartografía: Mapas y planos a escala.
- Arquitectura y Diseño: Maquetas y modelos.
- Fotografía y Video: Ampliación y reducción de imágenes.
- Ingeniería: Construcción de modelos.
- Arte: Perspectiva.
- Diseño Gráfico
Conexión con Homotecias:
Recordemos que una transformación geométrica que produce figuras semejantes es la homotecia. La razón de semejanza entre dos figuras homotéticas es igual a la razón de la homotecia en el caso que dicha homotecia sea positiva.
Teorema de Tales:
Recordemos el Teorema de Tales, que establece que si tres o más rectas paralelas son intersectadas por dos transversales, entonces los segmentos determinados sobre las transversales son proporcionales. Aunque ya hemos demostrado este teorema, es importante destacar que también se puede demostrar utilizando el concepto de homotecia. Esta es una muestra más de la estrecha relación entre la semejanza y las homotecias.
3. Razon de semejanza y razon de homotecia
Razón de Semejanza y Razón de Homotecia
Razón de Semejanza:
La razón de semejanza es la proporción constante entre las longitudes correspondientes de dos figuras semejantes. Es fundamental el orden en que se comparan las figuras:
- "Razón de semejanza de la figura S a la figura T":
- Significa que la figura T es la imagen (la figura transformada , ya sea ampliación o reduccion)
- La figura S es la preimagen (la figura original).
- La razón se calcula dividiendo una longitud en T (imagen) entre la longitud correspondiente en S (preimagen).
\[ \frac{imagen(T)}{preimagen(S)} \]
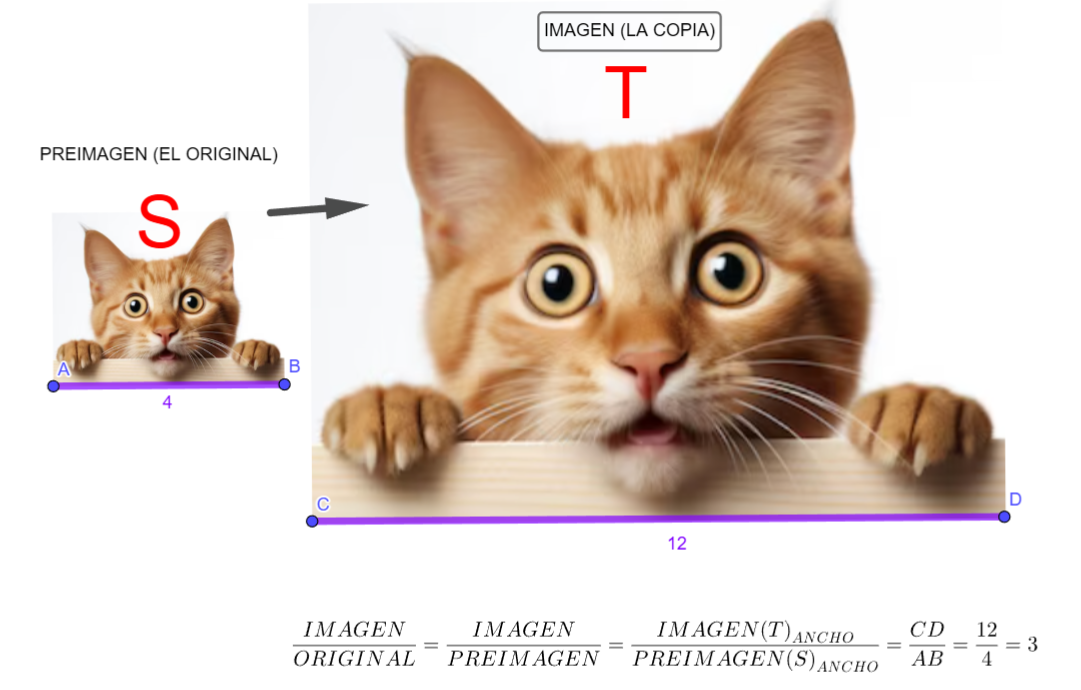
"Las medidas de la imagen son tres veces mas grande que las del original".
- "Razón de semejanza de la figura T a la figura S":
-
- Significa que la figura S es la imagen
- La figura T es la preimagen.
- La razón se calcula dividiendo una longitud en S (imagen) entre la longitud correspondiente en T (preimagen).
\[ \frac{imagen(S)}{original(T)} \]
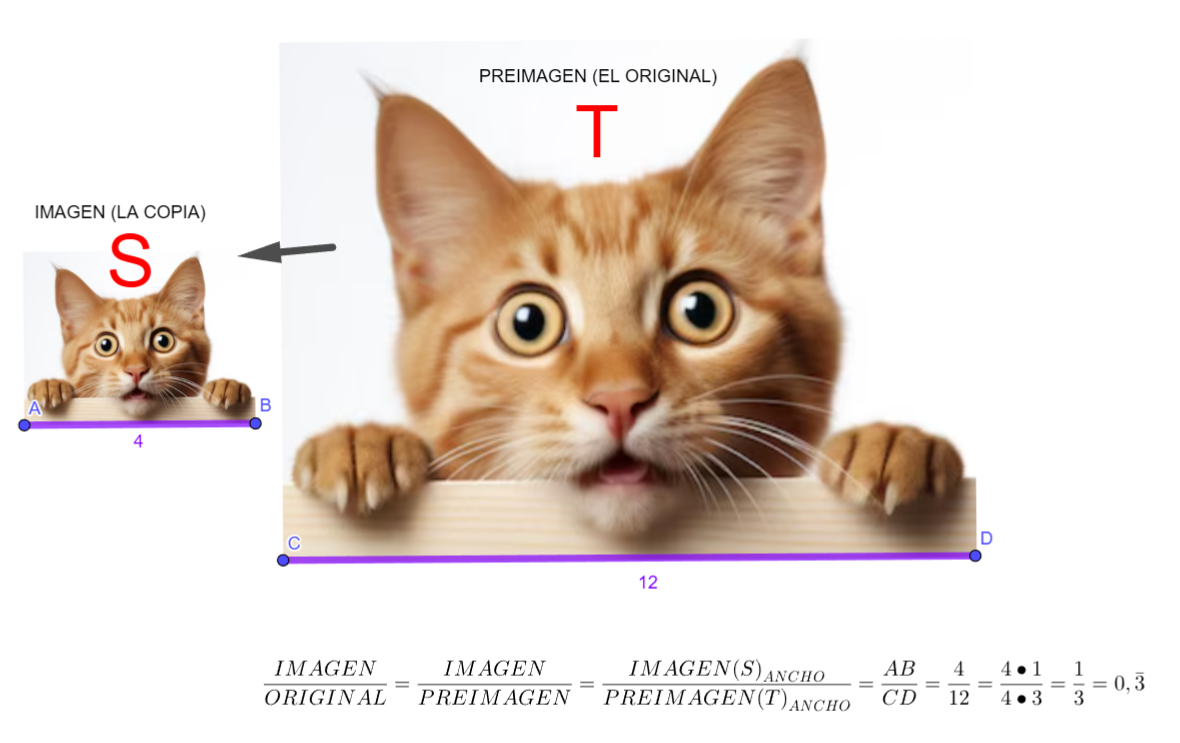
"Las medidas de la imagen son tres veces mas pequenas que las del original"
La razón de semejanza es siempre un número positivo, ya que representa una proporción entre longitudes. Si cambiamos el orden de la preimagen y la imagen, la razón de semejanza se invierte.
Ejemplo:
Sean dos triangulos ABC y A'B'C'
- El triángulo A'B'C' es semejante al triángulo ABC
- A'B' = 2 * AB,
Entonces:
- La razón de semejanza de ABC a A'B'C' es 2 (A'B'C' es el doble de grande).
- La razón de semejanza de A'B'C' a ABC es 1/2 (ABC es la mitad de grande).
Razón de Homotecia (k):
La razón de homotecia es el factor por el cual se multiplican las distancias desde un punto fijo (el centro de homotecia) para obtener una figura homotética. Indica:
- Magnitud del Escalamiento: El valor absoluto de k (|k|) determina el factor de escala.
- |k| > 1: Ampliación.
- 0 < |k| < 1: Reducción.
- |k| = 1: Congruencia.
- Dirección (Inversión): El signo de k:
- k > 0: La imagen está del mismo lado del centro de homotecia que la preimagen.
- k < 0: La imagen está del lado opuesto del centro (inversión).
Relación entre Razón de Semejanza y Razón de Homotecia:
Cuando dos figuras son homotéticas, la razón de semejanza entre ellas es igual al valor absoluto de la razón de homotecia (|k|). La homotecia garantiza la semejanza, y la razón de homotecia nos da, directamente (con su valor absoluto), la razón de semejanza.
Si dos figuras son simplemente semejantes, pero no sabemos si existe una homotecia que las relacione, solo podemos hablar de la razón de semejanza.
Ejemplos (Homotecia):
- k = 3: La figura homotética es tres veces más grande y está del mismo lado del centro. Razón de semejanza = 3.
- k = -1/2: La figura homotética es la mitad de grande y está invertida. Razón de semejanza = 1/2.
- k = -1: La figura homotética es una reflexión de la original. Razón de semejanza = 1.
En resumen: La razón de homotecia (k) describe completamente la transformación (escalamiento e inversión/dirección). La razón de semejanza, siempre positiva, solo indica la proporción entre los tamaños de las figuras, y es igual a |k| cuando las figuras son homotéticas. El orden en que se consideran la preimagen y la imagen es crucial para interpretar correctamente la razón de semejanza.
Ejercicios Conceptuales
- Verdadero o Falso (Justifica): "Si dos figuras son semejantes, entonces siempre son congruentes".
- Completar la frase: "La razón de semejanza de la figura A a la figura B es 3/4. Esto significa que la figura ________ es más grande, y cada longitud en la figura ___________ es _________ veces la longitud correspondiente en la figura ____________."
- Explicación: Dos amigos discuten. Uno dice que si dos rectángulos tienen todos sus ángulos iguales, entonces son semejantes. El otro dice que eso no es suficiente. ¿Quién tiene razón y por qué?
- Relación con Homotecia: Explica con tus propias palabras cómo se relacionan la razón de semejanza y la razón de homotecia cuando dos figuras son homotéticas. ¿Qué ocurre si la razón de homotecia es negativa?
Ejercicios Prácticos
- Dos triángulos, ABC y DEF, son semejantes. Se sabe que la razón de semejanza de ABC a DEF es 1/3. Si DE = 18 cm, calcula AB.
- En un triángulo rectángulo ABC, la altura desde el ángulo recto a la hipotenusa divide al triángulo en dos triángulos más pequeños. Demuestra que estos dos triángulos más pequeños son semejantes entre sí, y *determina la razón de semejanza entre ellos* si los segmentos en que la altura divide a la hipotenusa miden 4 cm y 9 cm.
- Dos triángulos, PQR y STU, son semejantes. La razón de semejanza de PQR a STU es 2/5. Si PQ = 6 cm, QR = 8 cm, y PR = 10 cm, calcula las longitudes de los lados de STU. *Expresa las longitudes de los lados de STU usando la razón de semejanza.*
- Dos pentágonos regulares son semejantes. Si la razón de semejanza del pentágono mayor al menor es 5/2, y el perímetro del pentágono menor es 30 cm, calcula la longitud del lado del pentágono mayor.
- Un arquitecto construye una maqueta de un edificio. La razón de semejanza de la maqueta al edificio real es 1/100. Si la altura de la maqueta es de 65 cm, ¿cuál es la altura real del edificio (en metros)? Si una ventana en el edificio real mide 2.5 metros de alto, ¿cuánto medirá la altura de la ventana correspondiente en la maqueta?
- Tienes una fotografía y la proyectas en una pantalla. La razón de semejanza de la imagen proyectada a la fotografía original es 5. Si el ancho de la fotografía original es de 12 cm, ¿cuál es el ancho de la imagen proyectada? Si quieres que la imagen proyectada tenga un ancho de 1.80 metros, ¿cuál debería ser la razón de semejanza entre la imagen proyectada y la fotografía original?
- Un árbol y un poste son perpendiculares al suelo. El árbol mide *h* metros y el poste 3 metros. En cierto momento del día, la razón de semejanza entre el triángulo formado por el árbol y su sombra y el triángulo formado por el poste y su sombra es 4. Si la sombra del poste mide 2.5 metros, ¿cuánto mide la sombra del árbol? ¿Cuánto mide el árbol?
- Se da un triangulo ABC, y un punto P. Se realiza una homotecia con centro en P. Dibuja una figura homotética A'B'C' si la razón de semejanza de A'B'C' a ABC es 3/2.
Problemas de Aplicación
- El telescopio casero: Quieres construir un telescopio casero... Si la distancia focal de la lente objetivo es 100 cm y la distancia focal de la lente ocular es 5 cm, ¿cuál es la *razón de semejanza* entre la imagen final que ves y el objeto real (muy lejano)?
- La cámara oscura: Una cámara oscura... Si un objeto de 1 metro de altura, situado a 5 metros del orificio, produce una imagen de 10 cm de altura en la pared opuesta, ¿cuál es la *razón de semejanza* entre la imagen y el objeto real? ¿A qué distancia está la pared opuesta del orificio?
- Estimación de alturas: Un método antiguo para estimar la altura de un árbol... Supón que tus ojos están a 1.60 metros del suelo. Te colocas a 2 metros de un espejo, y el espejo está a 15 metros del árbol. ¿Cuál es la *razón de semejanza* entre el triángulo formado por tu vista y el espejo y el triángulo formado por el árbol y el espejo? ¿Cuál es la altura del árbol?
- Diseño de una rampa: Quieres diseñar una rampa... Se te pide que la *razón de semejanza* entre el triángulo formado por la rampa y un triángulo más pequeño de referencia (con altura 1 metro y base 5 metros) sea de 1/4. ¿qué longitud tendrá la rampa resultante?
4. Criterio AA de Semejanza de Triángulos
Criterio AA de Semejanza de Triángulos
Enunciado
El criterio AA (Ángulo-Ángulo) establece que si dos ángulos de un triángulo son congruentes a dos ángulos de otro triángulo, entonces los dos triángulos son semejantes.
Si dos triangulos tienen dos ángulos correspondientes del mismo tamaño , es logico deducir que la tercera pareja de ángulos tambien serán congruentes ya que deben sumar 180°, por lo tanto los tres ángulos son congruentes
Pero ahora se debe deducir que los lados correspondientes seán proporcionales....
Demostración Formal
Dados dos triángulos, ΔABC y ΔDEF, donde ∠A ≅ ∠D y ∠B ≅ ∠E, demostraremos que ΔABC ~ ΔDEF.
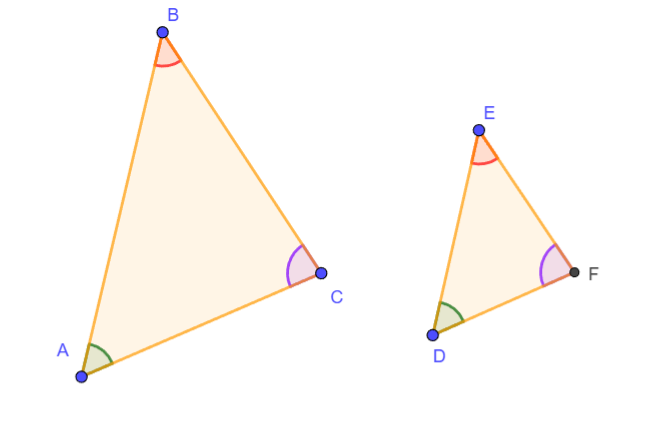
(Nota La siguiente demostracion supone que la primera figura es mas grande que la segunda, se podria extender los lados del primer triangulo en caso que el segundo sea mas grande y la demostracion seria valida igual, sin embargo para mayor claridad se eligio solo mostrar el primer caso "grande-chico" ya que el segundo seria trivialmente demostrable)
1.- Construcción:
Con ayuda de un compaz Construimos un punto E' en AB y F' en AC tal que DE = AE' y DF = AF'. Esto crea un triángulo ΔAE'F'.
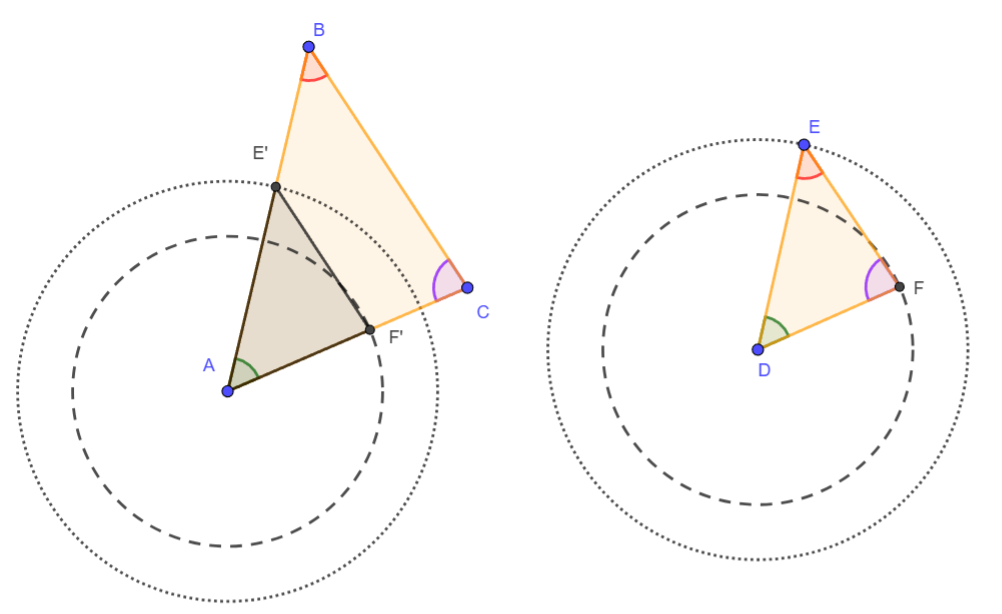
2.- Triángulos Congruentes:
El triángulo que se formó es de la misma forma y tamaño que el segundo triángulo (el mas pequeño de ambos) y esto lo podemos asegurar por un criterio de congruencia LAL
" ΔAE'F' ≅ ΔDEF por el postulado LAL (Lado-Ángulo-Lado)".
3.- Ángulos Correspondientes:
podemos conliur entonces que ∠E' ≅ ∠E (ángulos correspondientes de triángulos congruentes).

4.- Ángulos y Rectas Paralelas:
a) ∠B ≅ ∠E (dado, es decir es premisa antes de empezar a demostrar)
b) ∠E' ≅ ∠E (paso 3).
Por transitividad, ∠B ≅ ∠E', ya que ambos miden lo mismo (∠E )
Al ser ∠B y ∠E' ángulos correspondientes (recordar secantes entre paralelas), podemos afirmar que E'F' || BC.
5.- Usando el Teorema de Tales:
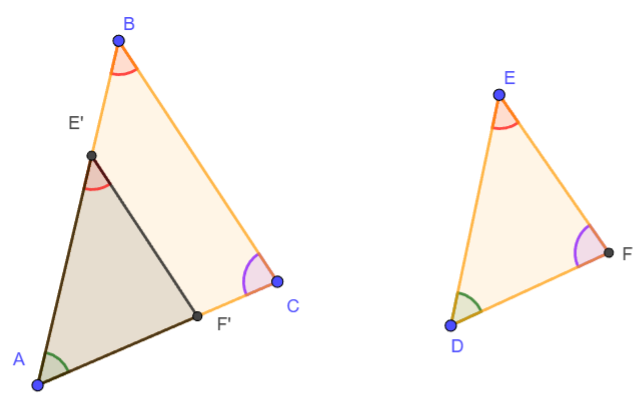
Al ser E'F' || BC implica que
\[ \frac{AE'}{AB} = \frac{AF'}{AC} = \frac{E'F'}{BC}
\]
6.- Sustitución:
Del paso 1 construcción sabiamos que AE' = DE y AF' = DF, asi que sustituyendo obtenemos
\[ \frac{DE}{AB} = \frac{DF}{AC} = \frac{E'F'}{BC} \]
Luego, como ΔAE'F' ≅ ΔDEF, E'F' = EF, por lo tanto:
\[ \frac{DE}{AB} = \frac{DF}{AC} = \frac{EF}{BC} \]
Definición de Semejanza:
Los lados correspondientes son proporcionales.(recien demostrado)
los ángulos son congruentes (explicado al principio)
entonces ΔABC ~ ΔDEF.
A continuación te presento La construccion que permite demostrar el criterio AA
puedes desplazar levemente los puntos para observar que la consistencia de dicha demostración es válida en todo tipo de triángulos
Ejemplos
Ejemplo 1: Triángulos Rectángulos
Dos triángulos rectángulos con un ángulo agudo de 30° son semejantes por AA (90° y 30°).
Ejemplo 2: Triángulos con Ángulos Compartidos
Un triángulo grande ΔABC y un triángulo más pequeño ΔADE (con DE || BC) son semejantes por AA (∠A compartido y ángulos correspondientes).
Ejemplo 3: Medición Indirecta
Si una vara de altura 'v' proyecta una sombra 's', y un edificio proyecta una sombra 'S', la altura del edificio 'H' se puede calcular como H = (v * S) / s, usando triángulos semejantes formados por la vara, el edificio y sus sombras.
5. Criterio LAL de Semejanza de Triángulos
Criterio LAL de Semejanza de Triángulos
Enunciado
El criterio LAL (Lado-Ángulo-Lado) establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo, y los ángulos comprendidos entre esos lados son congruentes, entonces los dos triángulos son semejantes.
Es decir, si tenemos dos triángulos, \( \triangle ABC \) y \( \triangle DEF \), y podemos verificar que \( \frac{AB}{DE} = \frac{AC}{DF} \) (es decir, que los lados \( AB \) y \( AC \) del primer triángulo son proporcionales a los lados \( DE \) y \( DF \) del segundo triángulo, respectivamente), y además, \( \angle A \cong \angle D \) (el ángulo entre \( AB \) y \( AC \) es congruente al ángulo entre \( DE \) y \( DF \)), entonces \( \triangle ABC \sim \triangle DEF \).
Demostración Formal
Dados dos triángulos, \( \triangle ABC \) y \( \triangle DEF \), donde \( \frac{AB}{DE} = \frac{AC}{DF} \) y \( \angle A \cong \angle D \), demostraremos que \( \triangle ABC \sim \triangle DEF \).
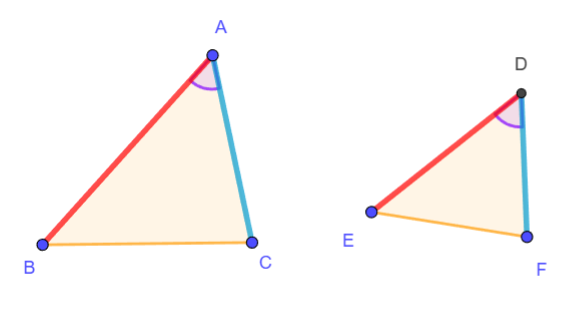
(Nota: Asumiremos, para simplificar la visualización, que \( \triangle ABC \) es mayor que \( \triangle DEF \). La demostración se puede adaptar fácilmente al caso contrario.)
Construcción:
Con ayuda de una regla, construimos un punto \( E' \) en \( AB \) tal que \( AE' = DE \). Luego, trazamos un segmento \( E'F' \) paralelo a \( BC \), donde \( F' \) está en \( AC \). Esto crea un triángulo \( \triangle AE'F' \).
Proporcionalidad (Teorema de Tales):
Como \( E'F' \parallel BC \), por el Teorema de Tales, sabemos que:
\[ \frac{AB}{AE'} = \frac{AC}{AF'} \]
Sustitución (usando la hipótesis):
Sabemos (por construcción) que \(AE' = DE\). También sabemos que \(\frac{AB}{DE} = \frac{AC}{DF}\). Podemos expresar esto como \(\frac{DE}{AB}=\frac{DF}{AC}\).
Sustituyendo \( AE' \) por \( DE \) en la proporción anterior:
\[ \frac{AB}{DE} = \frac{AC}{AF'} \]
Como \(\frac{DE}{AB} = \frac{DF}{AC}\), entonces, por transitividad:
\[ \frac{AC}{AF'} = \frac{AC}{DF} \]
Esto implica que \( AF' = DF \).
Triángulos Congruentes:
Ahora tenemos:
- \( AE' = DE \) (por construcción)
- \( AF' = DF \) (demostrado)
- \( \angle A \cong \angle D \) (dado)
Por el postulado LAL de congruencia de triángulos, podemos afirmar que \( \triangle AE'F' \cong \triangle DEF \).
Ángulos Correspondientes y Semejanza:
Como \( \triangle AE'F' \cong \triangle DEF \), sabemos que todos sus ángulos correspondientes son congruentes. En particular, \( \angle AE'F' \cong \angle E \).
Además, por construcción, como \(E'F' \parallel BC\), se tiene que \( \angle AE'F' \cong \angle B\)
Por transitividad, \( \angle B \cong \angle E \).
Ahora, en los triángulos originales \( \triangle ABC \) y \( \triangle DEF \), tenemos:
- \( \angle A \cong \angle D \) (dado)
- \( \angle B \cong \angle E \) (demostrado)
Por el criterio AA de semejanza, concluimos que \( \triangle ABC \sim \triangle DEF \).
En resumen:
Hemos construido un triángulo (\( \triangle AE'F' \)) congruente al triángulo más pequeño (\( \triangle DEF \)) dentro del triángulo más grande (\( \triangle ABC \)). Usando la proporcionalidad dada y el Teorema de Tales, demostramos que los lados del triángulo construido son proporcionales a los lados del triángulo grande. Finalmente, la congruencia de ángulos y el criterio AA nos permiten concluir que los dos triángulos originales son semejantes. ¡Hemos demostrado el criterio LAL!