1. Recordemos cosas de la Estadística

¿Qué es la Estadística?

La estadística es la ciencia que recolecta, organiza, analiza, interpreta y presenta datos para obtener conclusiones y tomar decisiones. Es una herramienta fundamental en muchos campos.

🌍 Ejemplos en el mundo real:

Un laboratorio analiza muestras de sangre para determinar la prevalencia de una enfermedad en la población.
Una encuestadora pregunta a personas sobre su intención de voto para predecir el resultado de las próximas elecciones.
Un agricultor usa datos históricos de lluvia para decidir cuándo es el mejor momento para plantar sus cultivos.

Tipos de Datos

Los datos son la materia prima de la estadística. Se clasifican principalmente en dos grandes grupos:

Tipo de Dato	Descripción	Subtipos y Ejemplos
Cualitativos (o Categóricos)	Describen características o cualidades que no pueden ser medidas con números.	Nominal: Categorías sin un orden específico (Ej: Estado civil, marca de auto). Ordinal: Categorías con un orden jerárquico (Ej: Nivel de educación, calificación de un servicio).
Cuantitativos (o Numéricos)	Representan cantidades y se pueden medir numéricamente.	Discretos: Se pueden contar y toman valores enteros (Ej: Número de hijos, errores en un examen). Continuos: Pueden tomar cualquier valor dentro de un rango (Ej: Peso, temperatura). De Intervalo: El cero es una referencia, no indica ausencia (Ej: Temperatura en °C, año de nacimiento). De Razón: El cero es absoluto e indica ausencia total (Ej: Ingreso mensual, altura de un edificio).

✍️ Ejercicio 1: Clasificación de Datos

Clasifica los siguientes datos:

Tipo de película favorita (comedia, drama, acción, etc.).
Número de estudiantes ausentes en una clase.
Temperatura máxima diaria en una ciudad.
Nivel de acuerdo con una afirmación (totalmente en desacuerdo, en desacuerdo, neutral, de acuerdo, totalmente de acuerdo).
Cantidad de dinero en una billetera.
Año de fabricación de un auto.
Peso de un paquete de arroz.
Número de habitaciones en una casa.

✍️ Ejercicio 2: Creación de Ejemplos

Para cada uno de los siguientes escenarios, proporciona un ejemplo de los tipos de datos indicados (nominal, ordinal, discreto, continuo, de intervalo y de razón):

Escenario 1: Una encuesta en un supermercado.
Escenario 2: El registro de pacientes en un consultorio médico.
Escenario 3: La medición de la calidad del aire en una ciudad.

Medidas de Tendencia Central

Nos entregan un valor "típico" o representativo de un conjunto de datos.

📐 Fórmulas Clave:

Media (Promedio): Es la suma de todos los datos dividida por el número total de datos. Se representa como $ \bar{x} $.
$ \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} $
Mediana: Es el valor que se encuentra justo en el centro de los datos, una vez que han sido ordenados de menor a mayor.
Moda: Es el valor que aparece con mayor frecuencia en el conjunto de datos. Un conjunto puede ser bimodal (dos modas) o multimodal.

⚠️ ¡Cuidado con los valores atípicos! La media es muy sensible a los valores extremos (muy altos o muy bajos). Un solo dato atípico puede "arrastrar" el promedio y hacer que no sea representativo del conjunto. La mediana, en cambio, es mucho más robusta frente a estos valores.

🧪 Ejemplo: Media (Promedio)

Es el valor que se obtiene al sumar todos los datos y dividirlos por la cantidad total. Su fórmula es: $ \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} $

Caso A: Para el conjunto de datos $ x = [1, 3, 5, 7] $, la media es:

$$\bar{x} = \frac{1+3+5+7}{4} = \frac{16}{4} = 4$$

Caso B: Para el conjunto de datos $ y = [100, 200, 600] $, la media es:

$$\bar{y} = \frac{100+200+600}{3} = \frac{900}{3} = 300$$

🧪 Ejemplo: Mediana (Valor Central)

Es el valor que se encuentra justo en el centro de un conjunto de datos, una vez que estos han sido ordenados de menor a mayor.

Caso Impar: Para el conjunto $ x = [10, 50, 30, 40, 20] $:

Ordenar: $ [10, 20, \textbf{30}, 40, 50] $
Identificar el centro: Con n=5 datos (un número impar), el valor central es el que está en la tercera posición. La Mediana es 30.

Caso Par: Para el conjunto $ y = [4, 8, 2, 6] $:

Ordenar: $ [2, \textbf{4}, \textbf{6}, 8] $
Identificar los dos centrales: Con n=4 datos (un número par), los valores centrales son 4 y 6.
Calcular el promedio: Se promedian los dos valores centrales: $ \frac{4+6}{2} = 5 $. La Mediana es 5.

⚠️ Dato importante: ¿Cómo encontrar la posición del dato central?

La forma de identificar el dato central para calcular la mediana depende directamente de si la cantidad total de datos $(n)$ en el grupo es par o impar.

Cuando el número de datos $(n)$ es IMPAR:
Hay un único valor central. La posición de este dato se encuentra con la fórmula: $$ \text{Posición} = \frac{n+1}{2} $$
Cuando el número de datos $(n)$ es PAR:
Hay dos valores en el centro. La mediana será el promedio de los datos que se encuentran en las posiciones: $$ \frac{n}{2} \quad \text{y} \quad \frac{n}{2} + 1 $$

🧪 Ejemplo: Moda (Valor más Frecuente)

Es el valor o los valores que aparecen con mayor frecuencia dentro de un conjunto de datos.

Caso A (Unimodal): En el conjunto $ [2, \textbf{2}, 3, 4, 5] $, el número que más se repite es el 2. Por lo tanto, la Moda es 2.

Caso B (Bimodal): En el conjunto $ [\textbf{1}, \textbf{1}, 2, \textbf{3}, \textbf{3}] $, tanto el 1 como el 3 se repiten dos veces, siendo los más frecuentes. Por lo tanto, es bimodal y sus Modas son 1 y 3.

⏱️ Problema 1: El Efecto de un Valor Atípico

Se registró el tiempo (en minutos) que tardaron 10 personas en completar una tarea:

25, 30, 28, 32, 27, 29, 31, 26, 33, 29

Calcula la media, mediana y moda de los tiempos.
¿Qué medida de tendencia central describe mejor el "tiempo típico"?
Si una persona adicional completa la tarea en 60 minutos, ¿cómo afectaría esto a la media, mediana y moda? ¿Cuál sería la más afectada?

📚 Problema 2: Representatividad de las Medidas

Se pregunta a un grupo de personas cuántos libros leyeron en el último año. Las respuestas son:

2, 0, 5, 1, 3, 2, 1, 0, 4, 6, 2, 3, 1, 0, 40

Calcula la media, mediana y moda.
¿Cuál es más representativa de la cantidad de libros que leyó la *mayoría*? Justifica.
¿Hay valores atípicos? ¿Cómo afectan a la media?

2. Introducción a la Estadística y la Variabilidad

Introducción a la Variabilidad

Variabilidad o Dispersión

La variabilidad, o dispersión, nos indica qué tan "esparcidos" o "alejados" están los datos entre sí o respecto a un valor central. Es un concepto clave en estadística.

La Importancia de Medir la Variabilidad

A menudo, cuando analizamos un conjunto de datos, nos centramos en la media (el promedio) para resumirlo todo en un solo número. Sin embargo, la media por sí sola puede ser muy engañosa. La variabilidad (o dispersión) nos cuenta el resto de la historia: cuán esparcidos o consistentes están los datos. Aquí te explico por qué es un concepto crucial.

1. La media sola puede ser engañosa 🤥

⚠️ Advertencia: Dos conjuntos de datos pueden tener la misma media, pero contar historias completamente opuestas. La variabilidad revela la verdadera distribución de los datos.

Ejemplo: Notas de dos cursos

Imagina que calculas la nota promedio de dos cursos de 5 estudiantes y en ambos el promedio final es un 5,5.

Curso A (baja variabilidad):
Sus promedios de notas son [5.5, 5.0, 6.0, 5.5, 5.5].
El rendimiento es muy consistente y predecible. Sabes qué esperar de ellos.
Curso B (alta variabilidad):
Sus promedios de notas son [2.0, 7.0, 4.5, 7.0, 7.0].
El rendimiento es impredecible y extremo. Tienes estudiantes con serias dificultades y otros que sobresalen.

Sin ver la dispersión, pensarías que ambos cursos son académicamente iguales, perdiendo información crucial para tomar decisiones pedagógicas, como ofrecer apoyo a los estudiantes del curso B que lo necesitan.

2. Mide la consistencia y la confiabilidad 🎯

🌍 Una baja variabilidad es sinónimo de calidad y predictibilidad. Esto es vital en la industria, las finanzas y la ciencia.

Ejemplo (Producción Industrial)

Una fábrica de tornillos busca que sus productos tengan un diámetro de 5 mm.

Fábrica A (baja variabilidad): Produce tornillos que miden entre 4.99 mm y 5.01 mm. Casi todos son perfectos, lo que se traduce en clientes satisfechos y cero devoluciones.
Fábrica B (alta variabilidad): Produce tornillos que miden entre 4.80 mm y 5.20 mm. Muchos no encajarán en su destino, generando pérdidas económicas y dañando la reputación de la marca.

En esta situación, sería deseable la más baja variabilidad posible.

Ejemplo (Inversiones Financieras)

Dos fondos de inversión tienen un retorno promedio anual de un 4%.

Fondo A (baja variabilidad): Su retorno anual ha oscilado entre el 2% y el 6%.
Fondo B (alta variabilidad): Su retorno ha fluctuado entre un -10% (pérdida) y un +18% (ganancia).

Nuevamente, ambos fondos promedian el mismo 4% de retorno anual, pero la variabilidad define la experiencia del inversionista. El Fondo A ofrece tranquilidad y previsibilidad a cambio de una rentabilidad positiva, baja pero segura. En cambio, el Fondo B representa la incertidumbre y el riesgo a cambio de la oportunidad de obtener ganancias mayores. La decisión final dependerá siempre del apetito por el riesgo de cada persona.

3. Permite comparaciones justas ⚖️

💡 Idea Clave: Para decidir entre opciones, la variabilidad es tan importante como el promedio. Te dice cuál opción es más fiable en el mundo real.

Ejemplo: Contratar un proveedor de internet

Vas a contratar un proveedor de internet para tu casa. Ambos prometen 200 Mbps en promedio.

Proveedor A (baja variabilidad): Tu velocidad casi siempre estará entre 190 y 210 Mbps. Es una conexión estable para tus videollamadas o clases online.
Proveedor B (alta variabilidad): A veces tendrás 400 Mbps, pero otras veces caerá a 10 Mbps, interrumpiendo tu trabajo justo en el momento más importante.

Si bien la idea de alcanzar 400 Mbps es tentadora, la alta variabilidad del Proveedor B significa que no tienes la seguridad de contar con una buena conexión durante tus clases o reuniones importantes. Para el uso diario, la consistencia del Proveedor A es mucho más valiosa.

4. Ayuda a identificar valores atípicos (outliers) ⚠️

🤓 Una variabilidad alta puede ser una "alarma" que te avisa de la existencia de datos anómalos (outliers) que están distorsionando la realidad y, por ende, el promedio.

Ejemplo: Tiempos de entrega

Analizas el tiempo de entrega de tus productos y el promedio es de 3 días, pero la desviación estándar (una medida de variabilidad) es muy alta.

Al revisar los datos en detalle, descubres que el 95% de los pedidos llega en 1-2 días, pero unos pocos tardaron 15 días por una huelga de transporte.

Esos valores atípicos (los de 15 días) inflan artificialmente el promedio y la variabilidad. Sin detectarlos, podrías pensar que tu logística es mala en general, cuando en realidad el problema fue un evento aislado y específico que debes gestionar de forma diferente.

🤓 ¿Por qué es importante medir la variabilidad?

Con la misma media, dos grupos pueden comportarse muy distinto pero si la dispersión difiere entonces se afecta la confiabilidad de las predicciones de cada grupo.

📊 Nos ayuda a comparar conjuntos con datos de la misma naturaleza.
🎯 Permite detectar si los datos que analizamos son consistentes o muy dispersos.
⚠️ Una media sin considerar la variabilidad puede ser engañosa.

✍️ Problema 1: Análisis de Distribución

Observa la siguiente distribución de datos y responde:

12, 15, 18, 18, 20, 21, 21, 21, 25, 30

Indica la media de la distribución.
Identifica los valores en los "extremos" de la distribución.
Identifica el sector donde hay una mayor concentración de datos.

🏀 Problema 2: Rendimiento de Equipos

Dos equipos de baloncesto registran sus puntajes en los últimos 5 partidos:

Equipo A: 85, 90, 88, 92, 80

Equipo B: 75, 105, 80, 95, 85

Calcula la media de los puntajes de cada equipo.
Argumenta: ¿qué equipo tiene mayor variabilidad en sus puntajes? ¿Por qué?

Problema 3: Grupos de estudiantes

Observa los siguientes gráficos de edades de estudiantes en dos grupos:

🟩 Grupo A	🟧 Grupo B

Argumenta: ¿qué grupo de estudiantes presenta una mayor variabilidad en sus puntajes? ¿Por qué?

3. Organización de Datos en Tablas e Interpretación Gráfica

Organización de Datos en Tablas e Interpretación Gráfica

🤓 Nota del Profesor: Antes de poder analizar qué tan "dispersos" están nuestros datos, primero debemos ser capaces de ordenarlos y visualizarlos de manera efectiva. Las tablas y los gráficos son nuestras herramientas principales para transformar una lista caótica de números en información útil.

Tipos de Tablas de Frecuencias

Dependiendo de la naturaleza de los datos, usamos distintas tablas para organizarlos.

Tipo de Tabla	Uso Principal	Ejemplo de Datos
tabla de registros o datos sueltos	Cuando hay un registro de cada uno de los datos y no han sido agrupados.	Sueldo específico de cada trabajador, registros de RUT.
Frecuencias para Datos no Agrupados	Cuando tenemos un número manejable de valores distintos que se repiten.	Notas de un curso (valores del 1 al 7), número de hijos por familia.
Frecuencias para Datos Agrupados	Cuando tenemos muchos valores distintos o son datos continuos.	Alturas de personas, peso de objetos, tiempo de espera en una fila.

Ejemplos de Tablas para Organizar Datos

🧪 Ejemplo: Tabla de Datos Simple

En estos registros de altura no hay valores repetidos.

Datos: Alturas (cm) de 5 estudiantes.

Estudiante	Altura (cm)
1	160
2	165
3	170
4	172
5	168

🧪 Ejemplo: Tabla de Frecuencias (Datos no Agrupados)

Aqui hay edades que se repiten, asi que se muestra cada edad una sola vez y su frecuencia respectiva (cuántas veces aparece).

Datos: Edades de 10 estudiantes: 20, 22, 20, 21, 22, 20, 23, 22, 20, 21.

Edad	Frecuencia (f)	Frecuencia Relativa (%)
20	4	40%
21	2	20%
22	3	30%
23	1	10%
Total	10	100%

🧪 Ejemplo: Tabla de Frecuencias (Datos Agrupados)

Aqui con 40 estudiantes hay muchas estaturas distintas mejor las agrupamos en intervalos o clases.

Datos: Alturas (cm) de 40 estudiantes.

Intervalo de Altura (cm)	Frecuencia (f)
150 - 159	5
160 - 169	12
170 - 179	15
180 - 189	8
Total	40

💡 ¿Cuándo agrupar en intervalos?

Agrupar datos en intervalos o "clases" es útil para simplificar un conjunto de datos grande y continuo. Al hacerlo, recuerda estas reglas generales:

Todos los intervalos deben tener la misma amplitud.
Los intervalos no deben superponerse.
Deben cubrir todo el rango de tus datos, desde el mínimo hasta el máximo.
Una buena práctica es usar entre 5 y 15 intervalos (regla práctica: raíz cuadrada del número de datos).

Interpretación Visual de la Dispersión

Los gráficos nos permiten "ver" la dispersión de los datos de un solo vistazo.

Histogramas

Un histograma nos muestra la forma de la distribución de los datos. Observando su forma, podemos estimar visualmente la dispersión:

Un histograma alto y estrecho indica baja dispersión (datos muy concentrados alrededor de la media).
Un histograma ancho y plano indica alta dispersión (datos muy esparcidos).

Diagramas de Caja (Boxplots)

Estos diagramas son un resumen visual de cinco números clave y son excelentes para comparar la dispersión entre distintos grupos.

📐 Componentes de un Diagrama de Caja:

Mediana (Q2): La línea que divide la caja en dos.
Caja: Contiene el 50% central de los datos. Sus bordes son el primer cuartil (Q1) y el tercer cuartil (Q3).
Rango Intercuartílico (IQR): Es el ancho de la caja (Q3 - Q1). Un IQR más grande implica mayor dispersión en el centro de los datos.
Bigotes: Las líneas que se extienden desde la caja. Indican la dispersión de los datos fuera del 50% central.
Valores Atípicos (Outliers): Puntos individuales fuera de los bigotes, que representan valores inusualmente altos o bajos.

🧪 Ejemplo: Comparación de Boxplots

Analicemos la dispersión de tres conjuntos de datos (j, k, l) a través de sus diagramas de caja.

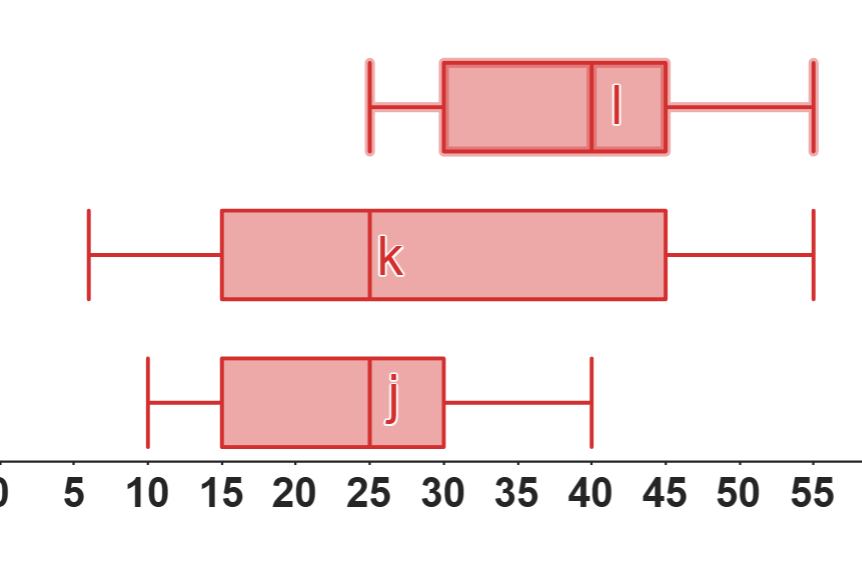
A continuación, se resumen las diferencias clave que podemos observar:

Característica	j	k	l
Rango (Dispersión Total)	Bajo (10 a 40)	Muy Alto (5 a 55)	Bajo (25 a 55)
Rango Intercuartílico (IQR)	Bajo (15)	Alto (30)	Bajo (15)
Simetría	Relativamente simétrico	Asimétrico a la derecha	Asimétrico a la izquierda
Conclusión	Datos consistentes y bajos.	Datos muy variables y dispersos.	Datos consistentes y altos.

Ejercicios y Problemas

✍️ Ejercicio 1: Tabla de Frecuencias

Las calificaciones de 20 estudiantes son: 7, 8, 6, 5, 9, 7, 8, 10, 6, 7, 7, 8, 9, 5, 6, 8, 7, 4, 9, 7. Organiza los datos en una tabla de frecuencias y calcula la frecuencia relativa de cada calificación.

Calificación	Frecuencia Absoluta	Frecuencia Relativa
4	1	0.05 (5%)
5	2	0.10 (10%)
6	3	0.15 (15%)
7	6	0.30 (30%)
8	4	0.20 (20%)
9	3	0.15 (15%)
10	1	0.05 (5%)
Total	20	1.00 (100%)

✍️ Ejercicio 2: Datos Agrupados

Los pesos (kg) de 30 paquetes son: 1.2, 1.5, 1.8, 2.1, 1.3, 1.6, 1.9, 2.0, 1.4, 1.7, 1.2, 1.5, 2.3, 1.8, 1.6, 1.4, 1.7, 2.0, 1.9, 1.3, 1.5, 1.8, 2.2, 1.7, 1.4, 1.6, 2.1, 1.9, 1.5, 1.8. Agrupa los datos en una tabla de frecuencias con intervalos de ancho 0.4 kg, comenzando en 1.2 kg.

Intervalo de Peso (kg)	Frecuencia
1.2 - 1.5	11
1.6 - 1.9	13
2.0 - 2.3	6
Total	30

✍️ Ejercicio 3: Interpretación de Histogramas

Observa los siguientes histogramas (descritos):

Histograma A: Simétrico y estrecho, centrado en 50.
Histograma B: Sesgado a la derecha, la mayoría de datos entre 20 y 40.
Histograma C: Ancho y plano, extendiéndose de 10 a 90.

¿Qué histograma tiene la mayor desviación estándar? ¿Y la menor?

✍️ Problema 1: Comparando la Dispersión

Se te presentan dos diagramas de caja:

Boxplot X: Mediana = 30, IQR = 10 (Q1=25, Q3=35), sin valores atípicos.
Boxplot Y: Mediana = 30, IQR = 20 (Q1=20, Q3=40), con un valor atípico en 60.

¿Qué boxplot representa datos con mayor dispersión? Justifica.

✍️ Problema 2: Análisis de Consultorios

Observa los gráficos (histograma y boxplot) de los tiempos de espera en dos consultorios médicos y responde:

Consultorio A

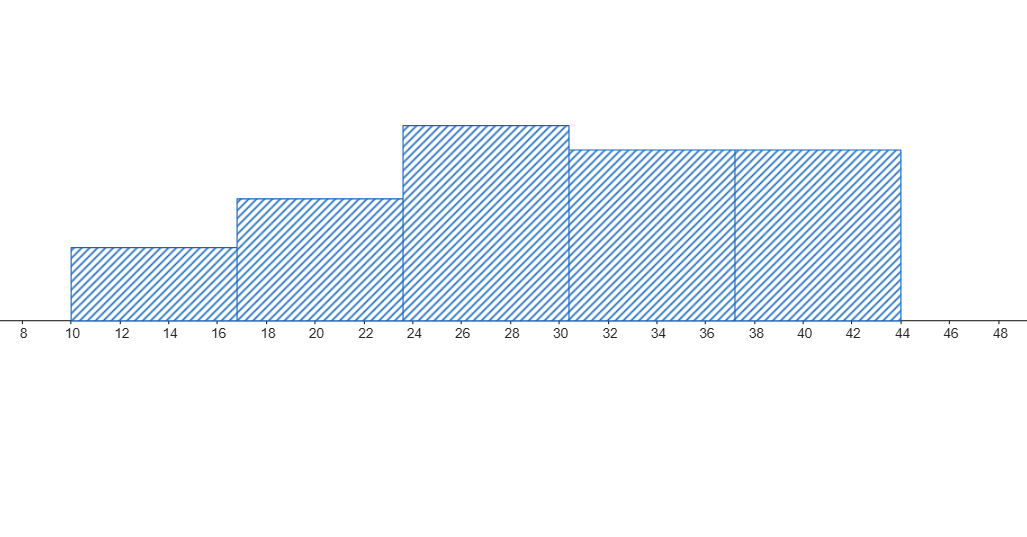
Consultorio B

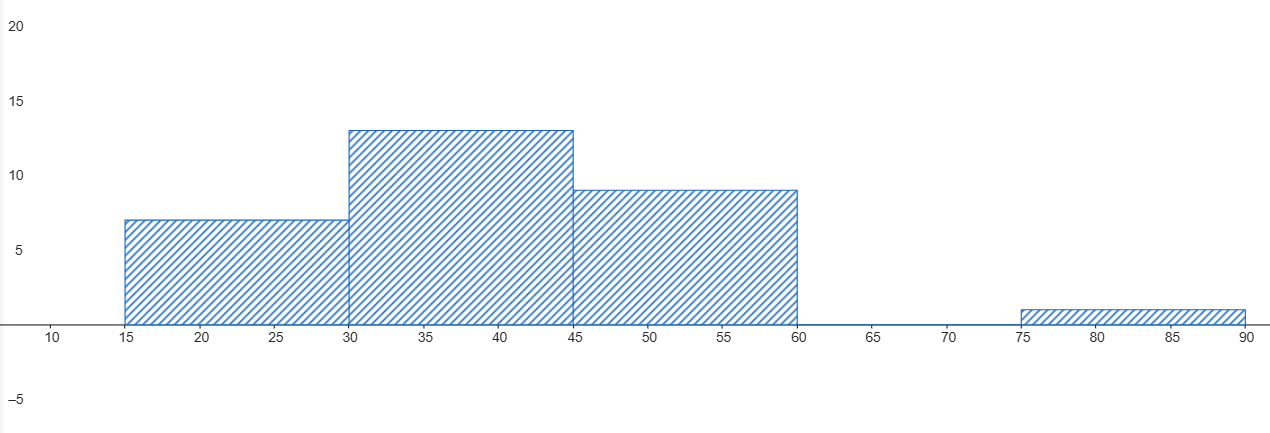
¿Qué consultorio tiene, en promedio, tiempos de espera más largos?
¿En qué consultorio los tiempos son más variables (mayor dispersión)?
Si tuvieras prisa, ¿a qué consultorio irías y por qué?

4. Organización de Datos en Tablas e Interpretación Gráfica

Organización de Datos en Tablas e Interpretación Gráfica

Importancia de la Organización de Datos

Antes de calcular medidas de dispersión (rango, varianza, desviación estándar), es crucial organizar los datos de manera clara y sistemática. Las tablas son una herramienta esencial para esto. Además, la representación gráfica (histogramas y diagramas de caja) nos da una idea visual rápida de la distribución y dispersión de los datos.

Tipos de Tablas

1. Tabla de Datos Simple (o Lista de Datos)

La forma más básica es listar los datos. Adecuado para conjuntos pequeños.

Ejemplo: Alturas (cm) de 5 estudiantes: 160, 165, 170, 172, 168

Estudiante	Altura (cm)
1	160
2	165
3	170
4	172
5	168

2. Tabla de Frecuencias

Para datos repetidos, una tabla de frecuencias es más eficiente. Muestra cada valor único y su *frecuencia* (cuántas veces aparece).

Ejemplo: Edades: 20, 22, 20, 21, 22, 20, 23, 22, 20, 21

Edad	Frecuencia (f)
20	4
21	2
22	3
23	1
Total	10

Frecuencia Relativa: Frecuencia de un valor dividida por el total. Se expresa como fracción, decimal o porcentaje.

Edad	Frecuencia (f)	Frecuencia Relativa	Frecuencia Relativa (%)
20	4	4/10 = 0.4	40%
21	2	2/10 = 0.2	20%
22	3	3/10 = 0.3	30%
23	1	1/10 = 0.1	10%
Total	10	1	100%

3. Tabla de Frecuencias con Datos Agrupados (Intervalos)

Para muchos datos diferentes, o datos continuos, se agrupan en *intervalos* o *clases*.

Ejemplo: Alturas (en cm) de 40 estudiantes (lista omitida por brevedad).

Intervalo de Altura (cm)	Frecuencia (f)
150 - 159	5
160 - 169	12
170 - 179	15
180 - 189	8
Total	40

Consideraciones al agrupar en intervalos:

Intervalos del mismo tamaño (amplitud).
Intervalos no superpuestos.
Cubrir todos los datos (mínimo a máximo).
Entre 5 y 15 intervalos (regla práctica: raíz cuadrada del número de datos).

Preparación de Datos para el Cálculo de Medidas de Dispersión

Con los datos en tablas (especialmente de frecuencias), es más fácil calcular las medidas:

Rango: Valor máximo - valor mínimo (o límites de los intervalos).
Varianza y Desviación Estándar:
- Datos sin agrupar: Usar la tabla para calcular la media y las desviaciones.
- Datos agrupados: Usar el *punto medio* (marca de clase) de cada intervalo.

Interpretación Visual de la Dispersión: Histogramas y Diagramas de Caja

Histogramas

Un histograma (gráfico de barras "pegadas" para representar continuidad) muestra la distribución de frecuencias de la variable. Permite *estimar* visualmente la media y la desviación estándar.

Estimación de la Media:

"Punto de equilibrio" del histograma.
Simétrico: media en el centro.
Asimétrico (sesgado): media desplazada hacia la "cola".

Estimación de la Desviación Estándar:

Relacionada con el "ancho" del histograma.
- Ancho y plano: *alta* desviación estándar (datos dispersos).
- Estrecho y alto: *baja* desviación estándar (datos concentrados).
Regla Empírica (aproximada, solo para distribuciones aproximadamente normales):
- Aprox. 68% de los datos: ±1 desviación estándar de la media.
- Aprox. 95% de los datos: ±2 desviaciones estándar de la media.
- Aprox. 99.7% de los datos: ±3 desviaciones estándar de la media.
Ejemplo: Si el 95% de los datos está entre 50 y 70, la desviación estándar es aproximadamente (70-50)/(2*2) = 5.

Advertencia: La regla empírica es solo una *aproximación* para distribuciones *aproximadamente normales*.

Ejemplos:

Ejemplo 1: Histograma alto y estrecho, centrado en 80. Media ≈ 80, Desviación estándar pequeña.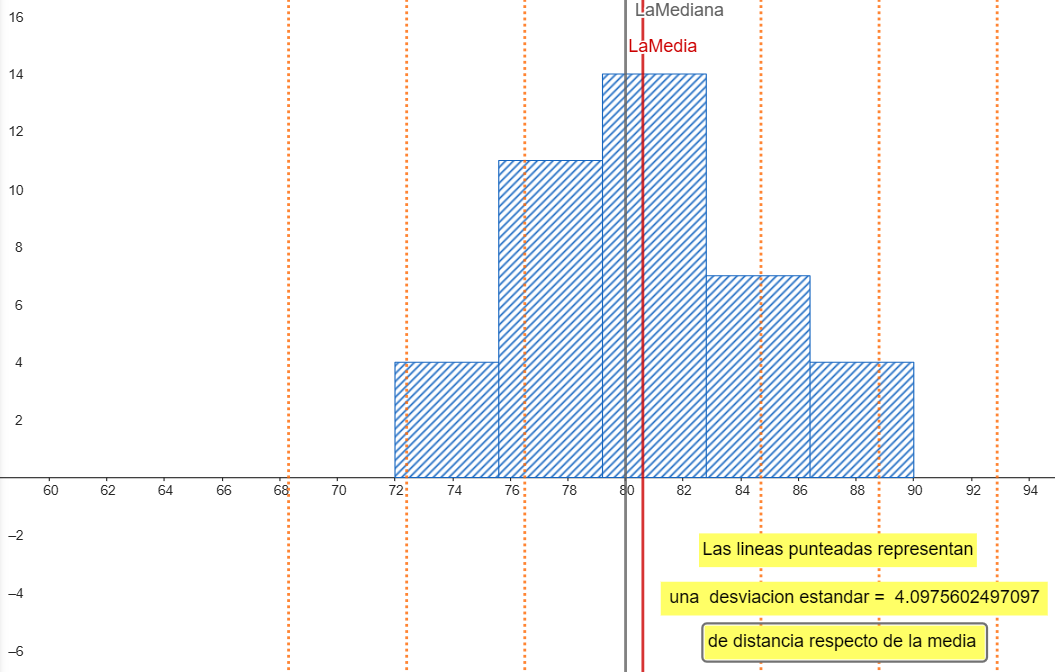

Ejemplo 2: Histograma sesgado a la izquierda. Media > Mediana. Desviación estándar mayor que si fuera simétrico.

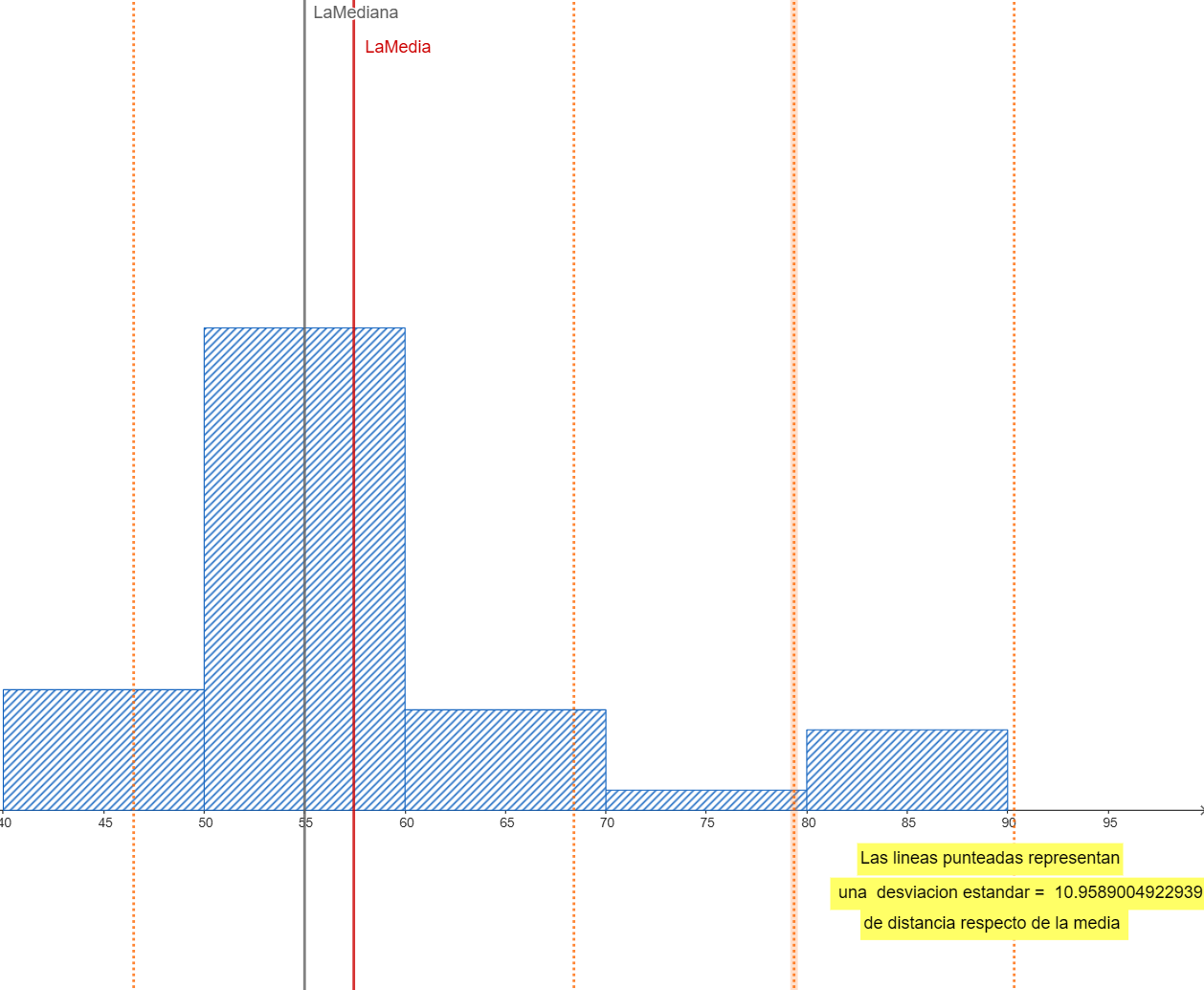
Ejemplo 3: Histograma ancho y plano, de 20 a 80. Media ≈ 50, Desviación estándar grande.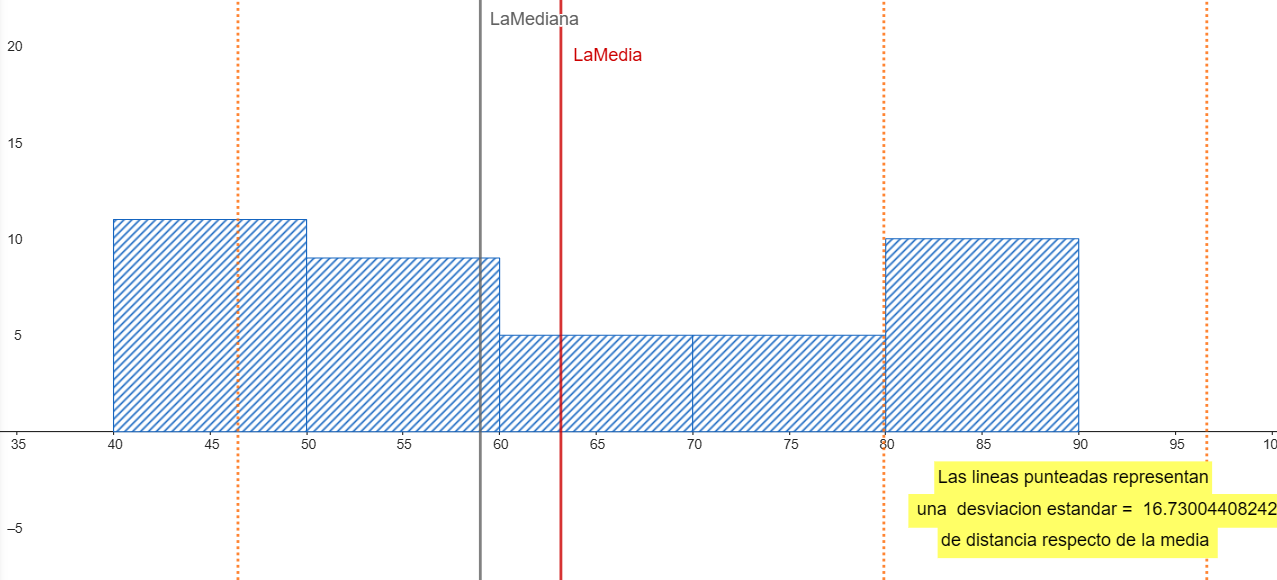

Diagramas de Caja (Boxplots)

Muestran un resumen de cinco números: mínimo, Q1 (primer cuartil), mediana, Q3 (tercer cuartil), máximo, y valores atípicos.

Mediana: Línea dentro de la caja.
Cuartiles (Q1 y Q3): Bordes de la caja. El 50% de los datos está *dentro* de la caja.
Rango Intercuartílico (IQR): Q3 - Q1. Medida de dispersión *resistente, es decir no se ve muy afectado por valores extremos como la desviacion estandar*.
Bigotes: Líneas desde la caja. Generalmente, hasta el máximo y mínimo de valores, siempre y cuando estos esten a distancia maxima de 1.5 * IQR desde los cuartiles Q1 o Q3 respectivos.
Valores Atípicos: Puntos individuales fuera de los bigotes, por sobre 1.5 * IQR.

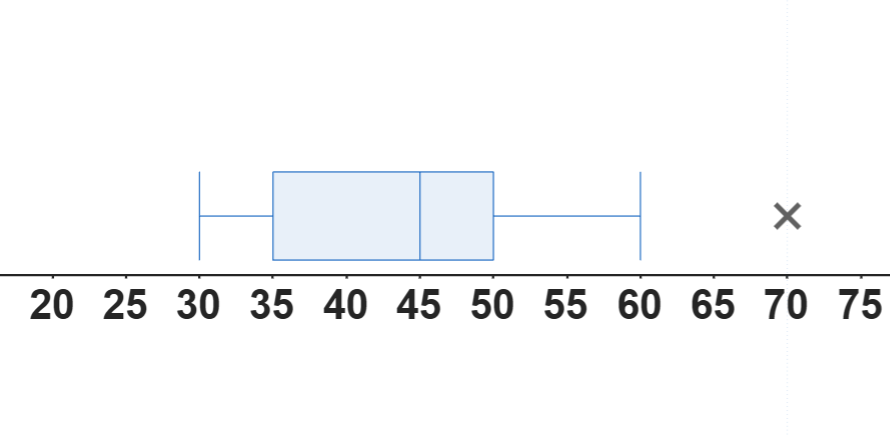
Estimación de la Desviación Estándar (aproximada, solo para distribuciones aproximadamente normales):

\[ \text{Desviación estándar} \approx \frac{IQR}{1.35} \]

Advertencia: Aproximación para distribuciones *aproximadamente normales*.

Ejemplo: Mediana = 60, Q1 = 50, Q3 = 70, Bigotes hasta 40 y 80, valor atípico en 95.

Mediana ≈ 60.
IQR = 70 - 50 = 20.
Si suponemos normalidad, Desviación estándar ≈ 20 / 1.35 ≈ 14.8.
Valor atípico: 95.

Comparación de Boxplots: Comparar el *ancho de las cajas* (IQR) y la *longitud de los bigotes*. Cajas más anchas y bigotes más largos indican mayor dispersión.

Ejemplo:

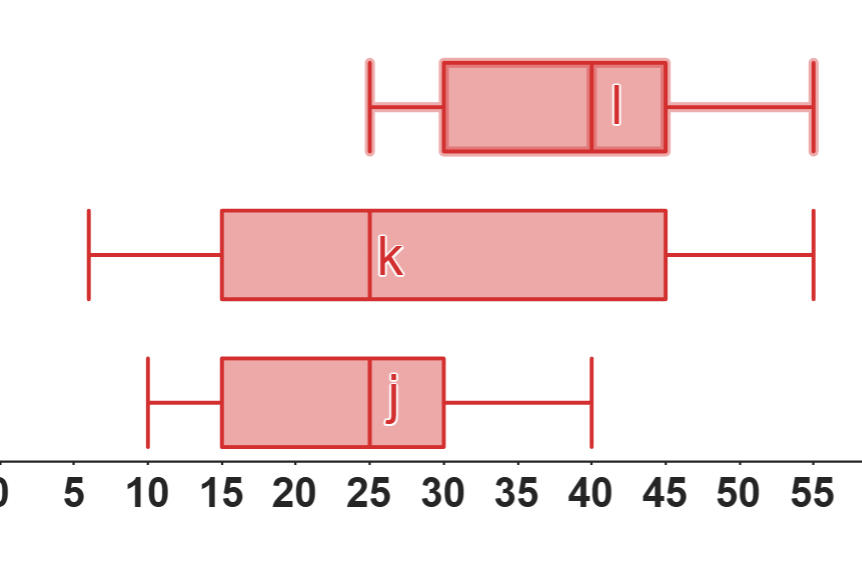
📊 Similitudes:

Mediana Común:
- Los conjuntos j y k tienen la misma mediana (25), lo que indica una tendencia central similar en estos dos conjuntos de datos.
Rango Similar:
- Los conjuntos j y l tienen un rango de 30 unidades (40 - 10 y 55 - 25 respectivamente), lo que indica una dispersión similar en el rango completo de los datos.
Rango Intercuartílico (IQR) Igual:
- Tanto j como l tienen un IQR de 15 (30 - 15 y 45 - 30), mostrando una variabilidad similar en el 50% central de sus datos.
Bigotes de Longitud Similar:
- Los bigotes del conjunto j y l son simétricos y tienen aproximadamente la misma extensión, indicando una distribución equilibrada de los datos fuera del IQR.

📈 Diferencias:

Característica	j	k	l
Rango (Máximo - Mínimo)	30 (10 a 40)	50 (5 a 55)	30 (25 a 55)
Rango Intercuartílico (IQR)	15 (15 a 30)	30 (15 a 45)	15 (30 a 45)
Asimetría	Relativamente simétrico	Asimetría a la derecha, ya que la mediana está cerca de Q1	Asimetría a la izquierda, con la mediana más cerca de Q3
Concentración de Datos	Datos más bajos (10 a 40)	Datos muy dispersos (5 a 55)	Datos más altos (25 a 55)
Mediana	25	25	40
Extremos de Bigotes	Mínimo en 10, Máximo en 40	Mínimo en 5, Máximo en 55	Mínimo en 25, Máximo en 55

🔍 Resumen de Diferencias:

Dispersión:
- k tiene la mayor dispersión general (mayor rango e IQR).
- j y l tienen una dispersión similar en el rango total, pero con diferencias en la tendencia central.
Ubicación de la Mediana:
- j y k comparten la misma mediana (25), mientras que l tiene una mediana significativamente más alta (40).
Distribución de los Datos:
- j: Datos concentrados en la parte inferior del rango.
- k: Gran dispersión con sesgo hacia la derecha.
- l: Datos concentrados en la parte superior del rango con un sesgo a la izquierda.

🎯 Conclusión:

Si buscas consistencia, el conjunto j es el más estable.
Para mayor rango de datos y variabilidad, el conjunto k es el indicado.
Si prefieres valores más altos en general, el conjunto l es el mejor representante.

Ejercicios y Problemas

Ejercicio 1: Los siguientes datos son calificaciones de 20 estudiantes (escala de 0 a 10):

7, 8, 6, 5, 9, 7, 8, 10, 6, 7, 7, 8, 9, 5, 6, 8, 7, 4, 9, 7

Organiza los datos en una tabla de frecuencias simple.
Calcula la frecuencia relativa de cada calificación.

Calificación (xi)	Frecuencia Absoluta (fi)	Frecuencia Relativa (hi)
4	1	0.05
5	2	0.10
6	3	0.15
7	6	0.30
8	4	0.20
9	3	0.15
10	1	0.05
Total ( n )	20	1.00

Ejercicio 2: Los siguientes datos son pesos (en kg) de 30 paquetes:

1.2, 1.5, 1.8, 2.1, 1.3, 1.6, 1.9, 2.0, 1.4, 1.7, 1.2, 1.5, 2.3, 1.8, 1.6, 1.4, 1.7, 2.0, 1.9, 1.3, 1.5, 1.8, 2.2, 1.7, 1.4, 1.6, 2.1, 1.9, 1.5, 1.8

Agrupa los datos en intervalos de ancho 0.2 kg (comenzando en 1.2 kg).
Construye una tabla de frecuencias con los intervalos.

Intervalo de Peso (kg)	Frecuencia (f)
1.2 - 1.3	4
1.4 - 1.5	7
1.6 - 1.7	6
1.8 - 1.9	7
2.0 - 2.1	4
2.2 - 2.3	2
Total	30

Ejercicio 3: Observa los siguientes histogramas (descritos):

Histograma A: Simétrico, centrado en 50, la mayoría de los datos entre 40 y 60.

Histograma B: Sesgado a la derecha, con la mayor parte de los datos entre 20 y 40, y una cola larga hasta 80.

Histograma C: Ancho y plano, extendiéndose desde 10 hasta 90.

¿Qué histograma tiene la mayor media? ¿La menor?
¿Qué histograma tiene la mayor desviación estándar? ¿La menor?
¿Cuál histograma se aproxima más a una distribución normal?

Ejercicio 4: Observa los siguientes diagramas de caja (descritos):

Boxplot X: Mediana = 30, Q1 = 25, Q3 = 35, Bigotes hasta 20 y 40, sin valores atípicos.

Boxplot Y: Mediana = 30, Q1 = 20, Q3 = 40, Bigotes hasta 10 y 50, un valor atípico en 60.

¿Qué boxplot representa datos con mayor dispersión?
¿Cuál boxplot indica la presencia de un valor atípico?
Estima la desviación estándar para cada boxplot (asumiendo normalidad).

Problema 1: Se realiza una encuesta sobre la cantidad de horas que 50 personas dedican a ver televisión por semana. Los resultados son:

X= horas viendo TV = {1, 2, 2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12, 12, 13, 13, 13, 15, 16, 17, 18, 20, 21, 23}

Organiza los datos en una tabla de frecuencias con intervalos de ancho 5 horas ( comenzando en 0 horas).
¿Qué porcentaje de personas ve televisión entre 10 y 14 horas por semana?
¿Cuál es el intervalo con mayor frecuencia?

Intervalo de Horas	Frecuencia (f)
0 - 4	10
5 - 9	15
10 - 14	12
15 - 19	8
20 - 24	5
Total	50

Problema 2: Se te presentan los siguientes datos sobre el tiempo de espera en dos consultorios médicos: [Insertar aquí un histograma y un boxplot para cada consultorio, o una descripción detallada de cada uno]. Basándote en la información visual de los gráficos, responde:

Consultorio A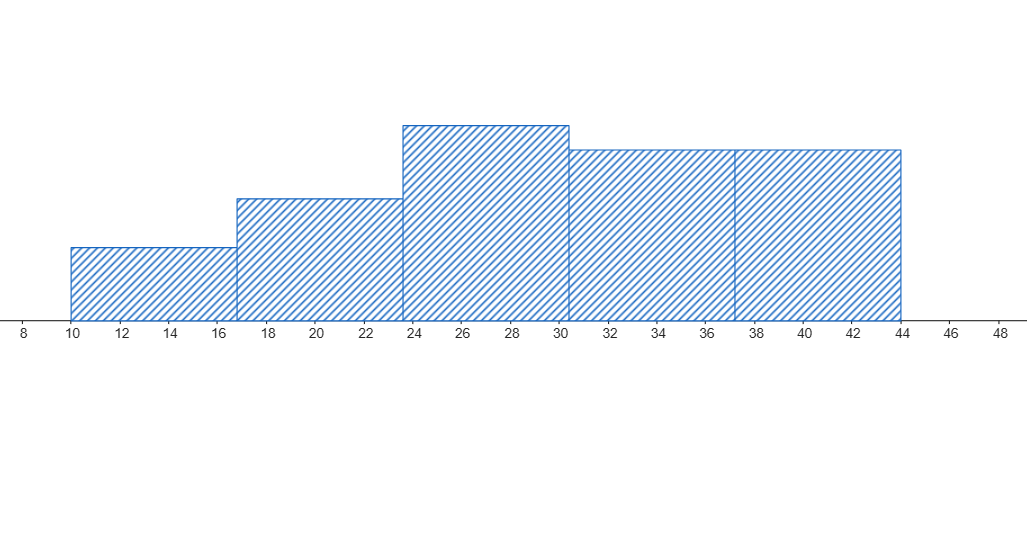

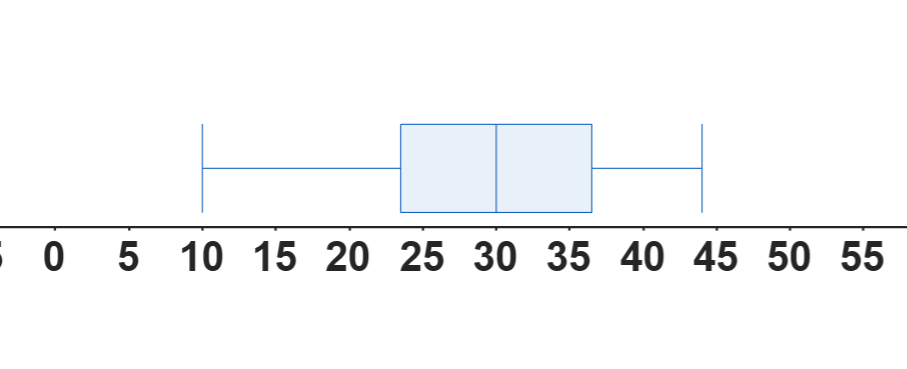
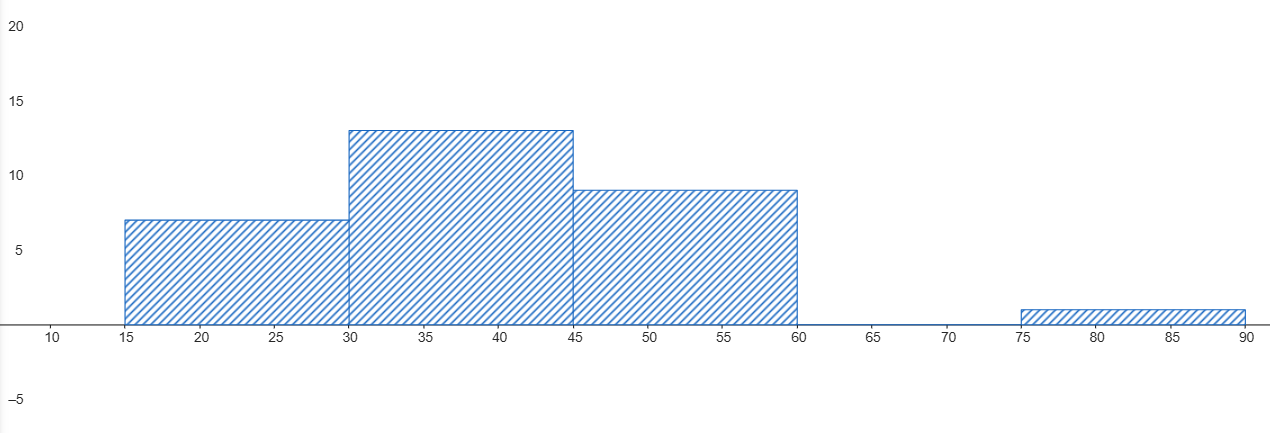
Consultorio B

¿Qué consultorio tiene, en promedio, tiempos de espera más largos?
¿En qué consultorio los tiempos de espera son más variables?
Si tuvieras prisa, ¿a qué consultorio irías? ¿Por qué?
¿Hay indicios de valores atípicos? De ser así, describe en que consiste.
Un analista afirma que: "Como el consultorio A tiene una menor desviación estándar, entonces es *imposible* que un paciente tenga que esperar más tiempo en el consultorio A que en el consultorio B". ¿Es verdadera o falsa esta afirmación? Justifica tu respuesta.

5. La Desviación Media (optativo complementario): Una Medida de Dispersión Intuitiva

La Desviación Media: Una Medida de Dispersión Intuitiva

Además del Rango y la Desviación Estándar, existe otra forma de medir la dispersión llamada Desviación Media (DM) o Desviación Absoluta Promedio. Esta medida responde de forma muy directa a la pregunta: "en promedio, ¿a qué distancia está cada dato de la media?".

📐 Fórmula de la Desviación Media

La Desviación Media es el promedio de los valores absolutos de las desviaciones de los datos con respecto a la media.

$ \Large DM = \frac{\sum_{i=1}^{n}|x_i - \bar{x}|}{n} $

$|x_i - \bar{x}|$: Es la distancia de cada dato a la media (siempre positiva).
$\sum$: Símbolo de sumatoria.
$n$: Número total de datos.

Cálculo Paso a Paso

Ejemplo: Goles por partido

Un futbolista ha anotado los siguientes goles en los últimos 5 partidos: {0, 1, 1, 2, 6}. Calculemos la desviación media para entender la consistencia de su rendimiento.

1. Calcular la media ($\bar{x}$):

$\bar{x} = \frac{0 + 1 + 1 + 2 + 6}{5} = \frac{10}{5} = 2$

La media es de 2 goles por partido.

2. Calcular las desviaciones absolutas:

Goles ($x_i$)	Desviación Absoluta $\|x_i - \bar{x}\|$
0	\|0 - 2\| = 2
1	\|1 - 2\| = 1
1	\|1 - 2\| = 1
2	\|2 - 2\| = 0
6	\|6 - 2\| = 4
Suma de Desviaciones:	8

3. Calcular la Desviación Media (DM):

$DM = \frac{\text{Suma de desviaciones absolutas}}{n} = \frac{8}{5} = 1.6$

Conclusión: La desviación media es de 1.6 goles. Esto significa que, en promedio, los goles que anota el futbolista en un partido se alejan 1.6 goles de su media de 2.

Desviación Media vs. Desviación Estándar

🤓 ¿Por Qué la Desviación Estándar es Más Común?

Si la Desviación Media es tan fácil de interpretar, ¿por qué se utiliza más la Desviación Estándar en estadística avanzada?

La razón principal es que la Desviación Estándar, al elevar las diferencias al cuadrado, posee propiedades matemáticas que la hacen más "compatible" con técnicas estadísticas complejas (como la inferencia o las regresiones). El valor absoluto, aunque intuitivo, es más difícil de manipular algebraicamente en esos contextos.

Sin embargo, la Desviación Media es una excelente herramienta para describir la dispersión de forma clara y es menos sensible a los valores extremos que la Desviación Estándar.

Ejercicios Propuestos

Ejercicio 1: Tiempos de Carrera

Los tiempos (en minutos) de un corredor en 6 días de entrenamiento fueron: {25, 28, 30, 32, 32, 35}. Calcula la desviación media de sus tiempos.

Problema 2: Consistencia de Notas

Dos estudiantes, Ana y Beto, tienen la misma nota promedio (8.0) en sus últimas 5 pruebas. Sus notas fueron:

Ana: {8, 8, 8, 8, 8}
Beto: {6, 7, 8, 9, 10}

Calcula la desviación media para cada estudiante y explica qué te dicen los resultados sobre su rendimiento.

6. Medidas de Dispersión: Rango, Varianza y Desviación Estándar

Medidas de Dispersión: Rango, Varianza y Desviación Estándar

Repaso: ¿Qué es la Dispersión?

La dispersión (o variabilidad) indica qué tan "esparcidos" están los datos alrededor de un valor central (como la media). Alta dispersión significa datos muy alejados; baja dispersión, datos agrupados cerca de la media.

El Rango

El rango es la medida de dispersión más simple, ya que solo considera los valores extremos de un conjunto de datos.

📐 Fórmula del Rango

Se calcula como la diferencia entre el valor máximo y el valor mínimo del conjunto de datos.

$ Rango = Valor \, Máximo - Valor \, Mínimo $

Ejemplos de Cálculo de Rango

Conjunto 1: {5, 8, 10, 12, 15} → Rango = 15 - 5 = 10

Conjunto 2: {23, 23, 24, 25, 26} → Rango = 26 - 23 = 3

⚠️ Limitaciones del Rango

Aunque es fácil de calcular, el rango tiene una gran desventaja: es muy sensible a valores atípicos (outliers). Un solo dato extremo puede cambiar drásticamente el rango y dar una idea equivocada de la dispersión general, ya que ignora cómo se distribuyen todos los demás datos.

La Varianza ($s^2$ o $\sigma^2$)

La varianza es una medida mucho más robusta que el rango. Mide la distancia promedio de cada dato respecto a la media, pero elevada al cuadrado. Aunque sus unidades cuadradas (ej. cm²) la hacen difícil de interpretar directamente, es la base para calcular la desviación estándar.

🤓 ¿Por qué se eleva al cuadrado la distancia?

Si simplemente sumáramos las distancias a la media (ej. 2-6 = -4 y 10-6 = 4), los valores negativos y positivos se cancelarían entre sí, y la suma total sería siempre cero. Al elevar cada distancia al cuadrado, convertimos todos los valores en positivos, asegurando que cada distancia contribuya a la medida total de dispersión.

📐 Procedimiento para Calcular la Varianza

Calcular la media ($\bar{x}$): Sumar todos los datos y dividir por la cantidad de datos .
Calcular las desviaciones: Restar la media a cada dato ($x_i - \bar{x}$).
Elevar al cuadrado cada desviación: Calcular $(x_i - \bar{x})^2$.
Sumar los cuadrados: Obtener la suma de todas las desviaciones al cuadrado: $\sum(x_i - \bar{x})^2$.
Dividir para promediar:
- Para una población completa, se divide por n.
- Para una muestra, se divide por n-1 (se conoce como "grados de libertad").

💡 Uso de Tablas para Organizar el Cálculo

Para conjuntos de datos más grandes, realizar el cálculo paso a paso puede ser desordenado. Usar una tabla es una estrategia muy eficiente para mantener los cálculos organizados y evitar errores.

Ejemplo de Cálculo de Varianza con Tabla Organizadora de Calculos

Calculemos la varianza para los datos: {2, 4, 6, 8, 10}.

Paso 1: Calcular la media.
$\bar{x} = \frac{2+4+6+8+10}{5} = \frac{30}{5} = 6 $

Paso 2: Construir la tabla y completar los cálculos.

Dato ($x_i$)	Desviación ($x_i - \bar{x}$)	Desviación al Cuadrado $(x_i - \bar{x})^2$
2	2 - 6 = -4	(-4)² = 16
4	4 - 6 = -2	(-2)² = 4
6	6 - 6 = 0	(0)² = 0
8	8 - 6 = 2	(2)² = 4
10	10 - 6 = 4	(4)² = 16
Suma de Cuadrados:		40

Paso 3: Calcular la varianza.

Varianza Muestral ($s^2$): Se divide por n-1.
$s^2 = \frac{40}{5-1} = \frac{40}{4} = 10$
Varianza Poblacional ($\sigma^2$): Se divide por n.
$\sigma^2 = \frac{40}{5} = 8$

📐 Fórmulas de la Varianza

Muestra: $ \Large s^2 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1} $

Población: $ \Large \sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n} $

Donde: $s^2$ es la varianza muestral, $\sigma^2$ es la varianza poblacional, $x_i$ son los datos, $\bar{x}$ es la media de la muestra, $\mu$ es la media de la población y $n$ es el número de datos.

Desviación Típica (o Estándar)

La desviación típica (o estándar) es la medida de dispersión más utilizada y la más intuitiva. Su gran ventaja es que, al ser la raíz cuadrada de la varianza, se expresa en las mismas unidades que los datos originales (ej. cm, kg, notas, etc.).

💡 ¿Por qué usar la Desviación Estándar?

Si la media de las notas de un curso es 5.5 y la desviación estándar es 0.5, podemos decir que, en promedio, las notas de los estudiantes se "desvían" 0.5 puntos de la media. Esta interpretación directa es mucho más clara que decir "la varianza es 0.25 notas al cuadrado".

📐 Fórmulas de la Desviación Estándar

Simplemente, es la raíz cuadrada de la varianza correspondiente.

Muestra: $ \Large s = \sqrt{s^2} = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}} $

Población: $ \Large \sigma = \sqrt{\sigma^2} = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n}} $

Ejemplo de Cálculo (continuación)

Usando las varianzas que calculamos en el ejemplo anterior:

Desviación Típica Muestral (s): $ s = \sqrt{10} \approx 3.16 $
Desviación Típica Poblacional ($\sigma$): $ \sigma = \sqrt{8} \approx 2.83 $

🌍 Interpretación en un Contexto Real

Imagina que un estudio sobre la altura de un curso arroja una media de 170 cm y una desviación estándar de 5 cm.

¿Qué significa "5 cm"? No significa que todos los estudiantes midan exactamente 5 cm más o menos que la media. Significa que 5 cm es la desviación "promedio" o esperada. Algunos se desviarán 1 cm, otros 8 cm, pero 5 cm es la medida que mejor representa la dispersión general del grupo.
¿Es mucho o poco? El valor de la desviación estándar (5 cm en este caso) se interpreta siempre en contexto. Por sí solo no es "bueno" o "malo". Se vuelve útil al comparar:
- Con otros grupos: Si la desviación estándar del curso del lado es de 2 cm, sabríamos que nuestro curso es más heterogéneo (diverso) en altura.
- Con un objetivo: Si estamos formando un equipo de baloncesto y buscamos jugadores altos y de estatura similar, una desviación de 5 cm podría ser considerada alta para nuestros propósitos.

💡 Regla General de Interpretación

Desviación estándar baja: Indica que los datos son muy consistentes y están agrupados cerca de la media.
Desviación estándar alta: Indica que los datos están mucho más dispersos y son menos predecibles.

Ejercicios y Problemas Propuestos

Ejercicio 1: Rango

Calcula el rango de los siguientes conjuntos de datos:

50, 60, 70, 80, 90
1, 3, 2, 7, 5, 4
120, 125, 118, 122, 124

Ejercicio 2: Varianza Muestral

Calcula la varianza muestral ($s^2$) de los datos: {3, 5, 7, 9, 11}, paso a paso.

Ejercicio 3: Desviación Típica Muestral

A partir del resultado del Ejercicio 2, calcula la desviación típica muestral ($s$).

Problema 1: Comparación de Grupos

Las edades de dos grupos de amigos son:

Grupo A: {18, 19, 20, 21, 22}

Grupo B: {15, 20, 18, 25, 17}

Calcula la media, el rango, la varianza y la desviación típica (muestral) para cada grupo.
¿Qué grupo tiene edades más homogéneas (menos dispersas)? Justifica usando los resultados.

Problema 2: Control de Calidad

Se mide la longitud (en cm) de 10 tornillos producidos por una máquina:

{5.0, 5.1, 4.9, 5.2, 5.0, 4.8, 5.1, 5.3, 4.9, 5.0}

Calcula la media, la varianza y la desviación típica (muestral).
Si se consideran aceptables los tornillos dentro de una desviación típica de la media (x̄ ± s), ¿cuál es el rango de longitudes aceptable?
¿Cuántos de los tornillos medidos están dentro de ese rango?

7. Cálculo de Varianza y Desviación Estándar para Datos Agrupados

Cálculo de Varianza y Desviación Estándar para Datos Agrupados

Repaso

La varianza ($s^2$ o $\sigma^2$) y la desviación estándar ($s$ o $\sigma$) son medidas fundamentales que nos indican qué tan dispersos o "alejados" están los datos con respecto a la media (el promedio). Cuando trabajamos con datos agrupados en intervalos (por ejemplo, "personas entre 20 y 30 años"), no conocemos el valor exacto de cada dato, por lo que usamos fórmulas adaptadas.

📐 Procedimientos y Fórmulas Clave

Para poder operar, necesitamos un valor que represente a cada intervalo. Usamos la marca de clase ($x_i$), que es simplemente el punto medio del intervalo.

Marca de Clase: \[ x_i = \frac{\text{Límite Inferior} + \text{Límite Superior}}{2} \]

A partir de ahí, las fórmulas son las siguientes (asumiendo que los datos son una muestra):

Media (promedio): \[ \bar{x} = \frac{\sum f_i \cdot x_i}{n} \] (Donde $f_i$ es la frecuencia de cada intervalo y $n$ el total de datos).
Varianza (muestral): \[ s^2 = \frac{\sum f_i (x_i - \bar{x})^2}{n-1} \]
Desviación Estándar (muestral): \[ s = \sqrt{s^2} \]

⚠️ ¡Cuidado con la División!

Un error muy común es confundir la fórmula de la varianza para una muestra (se divide por $n-1$) con la de una población (se divide por $N$). En la mayoría de los casos prácticos y ejercicios, trabajamos con muestras de una población más grande, por lo que usaremos $n-1$. ¡Presta atención al enunciado!

Cálculo Paso a Paso (Ejemplo Guiado)

Datos: Se midió la altura (en cm) de una muestra de 40 estudiantes, obteniendo la siguiente tabla de frecuencias.

Intervalo (cm)	Frecuencia ($f_i$)
[150 - 160)	5
[160 - 170)	12
[170 - 180)	15
[180 - 190)	8
Total	40

Para calcular la varianza y desviación estándar, construiremos una tabla que nos ayudará a organizar todos los cálculos. ¡Vamos paso a paso!

Tabla de Trabajo Inicial:

Comenzamos con esta tabla, donde solo tenemos los datos iniciales. Nuestro objetivo es completar las columnas vacías.

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[150 - 160)		5
[160 - 170)		12
[170 - 180)		15
[180 - 190)		8
Total		40

Tabla de Cálculo Completa:

Ahora, completamos cada columna secuencialmente hasta obtener todos los valores necesarios para nuestras fórmulas.

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[150 - 160)	155	5	775	-16.5	272.25	1361.25
[160 - 170)	165	12	1980	-6.5	42.25	507
[170 - 180)	175	15	2625	3.5	12.25	183.75
[180 - 190)	185	8	1480	13.5	182.25	1458
Total		$n=40$	$\sum = 6840$			$\sum = 3510$

Cálculos finales:

Media: $\bar{x} = \frac{6840}{40} = 171$ cm

Varianza (muestral): $s^2 = \frac{3510}{40-1} = \frac{3510}{39} \approx 90 \text{ cm}^2$

Desviación Estándar (muestral): $s = \sqrt{90} \approx 9.49$ cm

Resultado: La altura promedio es de 171 cm, con una desviación estándar de aproximadamente 9.49 cm, lo que nos indica la dispersión típica de las alturas respecto a ese promedio.

💡 ¿Qué significa la Desviación Estándar en la práctica?

Una desviación estándar pequeña significa que la mayoría de los datos están muy agrupados cerca de la media (son muy consistentes). Una desviación estándar grande indica que los datos están más esparcidos y son más variables. Es una medida clave para comparar la consistencia entre diferentes conjuntos de datos.

Ejercicios y Problemas

Nivel 1:

Cálculos de varianza y Desviación estándar

Ejercicio 1: Edades en una Empresa

La siguiente tabla muestra la distribución de edades (en años) de los empleados de una empresa. Calcula la media, la varianza y la desviación estándar muestrales.

Edad (años)	Frecuencia
[20 - 30)	10
[30 - 40)	15
[40 - 50)	12
[50 - 60)	8
[60 - 70)	5

Tabla de Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[20 - 30)	25	10	250	-16.6	275.56	2755.6
[30 - 40)	35	15	525	-6.6	43.56	653.4
[40 - 50)	45	12	540	3.4	11.56	138.72
[50 - 60)	55	8	440	13.4	179.56	1436.48
[60 - 70)	65	5	322.5	23.4	547.56	2737.8
Total		50	2055			7722

Media: $\bar{x} = \frac{2055}{50} = 41.1$ años
Varianza: $s^2 = \frac{7722}{49} \approx 157.59$ años²
Desviación estándar: $s = \sqrt{157.59} \approx 12.55$ años

Ejercicio 2: Calificaciones de un Curso

Un profesor registra las calificaciones finales de su curso de estadística en la siguiente tabla. Considerando los datos como una muestra de todos sus estudiantes históricos, calcula la nota promedio, la varianza y la desviación estándar para evaluar el rendimiento y la consistencia del grupo.

Calificación	Nº de Estudiantes ($f_i$)
[1.0 - 2.0)	2
[2.0 - 3.0)	5
[3.0 - 4.0)	8
[4.0 - 5.0)	15
[5.0 - 6.0)	12
[6.0 - 7.0]	8

Tabla de Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[1.0 - 2.0)	1.5	2	3.0	-3.08	9.4864	18.9728
[2.0 - 3.0)	2.5	5	12.5	-2.08	4.3264	21.632
[3.0 - 4.0)	3.5	8	28.0	-1.08	1.1664	9.3312
[4.0 - 5.0)	4.5	15	67.5	-0.08	0.0064	0.096
[5.0 - 6.0)	5.5	12	66.0	0.92	0.8464	10.1568
[6.0 - 7.0]	6.5	8	52.0	1.92	3.6864	29.4912
Total		50	229.0			89.68

Media: $\bar{x} = \frac{229}{50} = 4.58$ puntos
Varianza: $s^2 = \frac{89.68}{49} \approx 1.83$ puntos²
Desviación estándar: $s = \sqrt{1.83} \approx 1.35$ puntos

Ejercicio 3: Control de Calidad en Pesaje de Café

Una empresa que envasa café toma una muestra de 80 paquetes de "250 gramos" para verificar la consistencia de sus máquinas. Los pesos reales (en gramos) se registran en la siguiente tabla. Calcula la desviación estándar para determinar qué tan preciso es el proceso de envasado.

Peso (gramos)	Nº de Paquetes ($f_i$)
[240 - 244)	7
[244 - 248)	15
[248 - 252)	35
[252 - 256)	18
[256 - 260]	5

Tabla de Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[240 - 244)	242	7	1694	-7.95	63.2025	442.4175
[244 - 248)	246	15	3690	-3.95	15.6025	234.0375
[248 - 252)	250	35	8750	0.05	0.0025	0.0875
[252 - 256)	254	18	4572	4.05	16.4025	295.245
[256 - 260]	258	5	1290	8.05	64.8025	324.0125
Total		80	19996			1295.8

Media: $\bar{x} = \frac{19996}{80} = 249.95$ gramos
Varianza: $s^2 = \frac{1295.8}{79} \approx 16.40$ gr²
Desviación estándar: $s = \sqrt{16.40} \approx 4.05$ gramos

8. Interpretación y Comparación con Medidas de Dispersión

Interpretación y Comparación con Medidas de Dispersión

Repaso: Medidas de Dispersión

Recordemos que las medidas de dispersión (rango, varianza, desviación estándar) nos indican qué tan "esparcidos" o "concentrados" están los datos alrededor de la media. Son fundamentales para comprender la variabilidad de un conjunto de datos.

Interpretación Conjunta de Media y Desviación Estándar

La media y la desviación estándar se interpretan *juntas* para tener una idea completa de la distribución de los datos. La media nos da el "centro" y la desviación estándar nos dice qué tan "anchos" son los datos alrededor de ese centro.

Ejemplo:

Conjunto A: Media = 50, Desviación estándar = 5
Conjunto B: Media = 50, Desviación estándar = 15

Ambos conjuntos tienen la misma media (50), pero el Conjunto B tiene una desviación estándar mucho mayor. Esto significa que:

En el Conjunto A, la mayoría de los datos estarán relativamente cerca de 50 (probablemente entre 45 y 55, o entre 40 y 60, si consideramos dos desviaciones estándar).
En el Conjunto B, los datos estarán mucho más dispersos. Es más probable encontrar valores significativamente más alejados de 50 (por ejemplo, valores por debajo de 35 o por encima de 65).

Comparación de Conjuntos de Datos

Podemos usar la media y la desviación estándar para comparar diferentes conjuntos de datos, incluso si tienen unidades diferentes (aunque en ese caso, es mejor usar el coeficiente de variación, que veremos más adelante).

Ejemplo (mismas unidades): Dos clases rinden el mismo examen:

Clase X: Media = 75, Desviación estándar = 8
Clase Y: Media = 75, Desviación estándar = 3

Conclusión: Ambas clases tienen el mismo promedio, pero la Clase Y tiene notas mucho más homogéneas (menos dispersas) que la Clase X.

Ejemplo (contexto diferente): Edades de dos grupos:

Grupo P: Media = 25 años, Desviación estándar = 2 años
Grupo Q: Media = 60 años, Desviación estándar = 10 años

Conclusión: Grupo P son más jovenes que el grupo Q, y además las edades del grupo P son mas homogeneas que el grupo Q

Diagramas de Caja y Bigotes (Boxplots)

Los diagramas de caja y bigotes (boxplots) son una forma visual de representar la dispersión de un conjunto de datos. No vamos a entrar en detalle sobre cómo construirlos, pero es importante saber *interpretarlos*.

Un boxplot muestra:

Mediana: Una línea dentro de la caja.
Cuartiles (Q1 y Q3): Los bordes de la caja. El 50% de los datos está *dentro* de la caja (entre Q1 y Q3). Este rango se llama *rango intercuartílico* (IQR).
"Bigotes": Líneas que se extienden desde la caja hasta los valores máximo y mínimo *dentro de un cierto rango* (generalmente, 1.5 veces el IQR).
Valores Atípicos (Outliers): Puntos individuales que se muestran *fuera* de los bigotes. Son valores inusualmente altos o bajos.

Ejemplo:

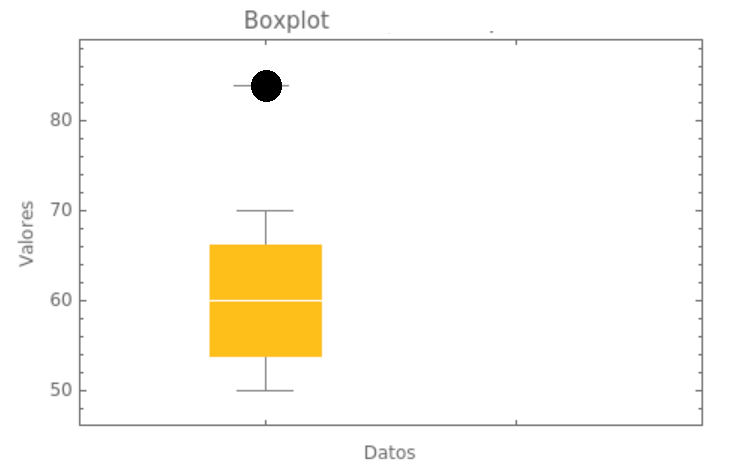
Lectura de la imagen

La mediana está en 60.
El primer cuartil (Q1) está en 55.
El tercer cuartil (Q3) está en 65.
Los "bigotes" se extienden hasta 50 y 70.
Hay un punto atípico en 85.

Interpretación:

El valor "típico" de los datos es alrededor de 60 (la mediana).
El 50% central de los datos está entre 55 y 65.
La mayoría de los datos están entre 50 y 70.
Hay un valor inusualmente alto (85) que se considera un valor atípico.

Valores Atípicos (Outliers)

Identificación (Regla General)

Una regla general para identificar valores atípicos es la regla del "1.5 veces el IQR":

Calcula el Rango Intercuartílico (IQR) = Q3 - Q1.
Calcula los "límites":
- Límite inferior = Q1 - 1.5 * IQR
- Límite superior = Q3 + 1.5 * IQR
Cualquier valor *fuera* de estos límites se considera un valor atípico.

Ejemplo:

Datos: 2, 3, 5, 7, 8, 9, 10, 12, 15, 25

Q1 = 4 (mediana de la primera mitad de los datos)
Q3 = 11 (mediana de la segunda mitad de los datos)
IQR = 11-4=7
Límite inferior: 4 - 1.5 * 7 = -6.5
Límite superior: 11 + 1.5 * 7 = 21.5

El valor 25 es un valor atípico, ya que es mayor que 21.5

Importancia

Los valores atípicos pueden deberse a errores de medición, errores de registro, o pueden ser valores válidos pero inusuales. Es importante identificarlos porque:

Pueden distorsionar las medidas de tendencia central (especialmente la media) y las medidas de dispersión.
Pueden indicar información importante sobre el proceso o fenómeno que se está estudiando.

No siempre se deben eliminar los valores atípicos. Hay que investigarlos y decidir si se eliminan, se corrigen o se mantienen, según el contexto.

Ejercicios y Problemas

Ejercicio 1: Dados los siguientes conjuntos de datos, interpreta la media y la desviación estándar en términos de la dispersión de los datos:

Conjunto X: Media = 10, Desviación estándar = 2
Conjunto Y: Media = 10, Desviación estándar = 8
Conjunto Z: Media = 100, Desviación estándar = 10

Ejercicio 2: Dados los siguientes boxplots (Diagramas de caja y bigotes)

Boxplot A:

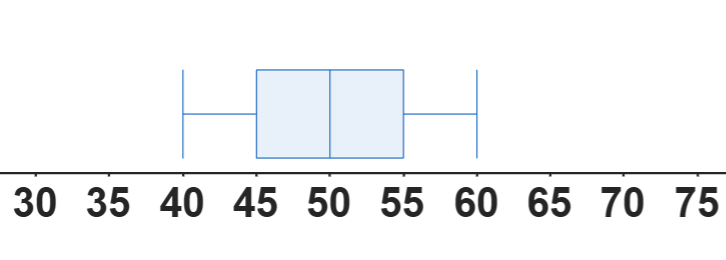
Boxplot B:

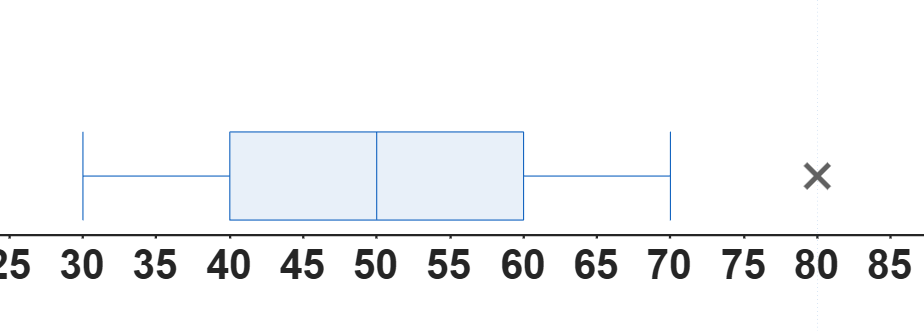
¿Qué boxplot representa datos con mayor dispersión?
¿Cuál boxplot indica la presencia de un valor atípico?

Ejercicio 3: Para el siguiente conjunto de datos, identifica si hay valores atípicos utilizando la regla del 1.5 * IQR:

1, 3, 5, 7, 8, 9, 10, 12, 14, 30

Paso	Descripción	Cálculo
1	Ordenar los datos	1, 3, 5, 7, 8, 9, 10, 12, 14, 30
2	Calcular Q1 (Primer Cuartil)	Mediana de la primera mitad (1, 3, 5, 7, 8): Q1 = (3 + 5) / 2 = 4
3	Calcular Q3 (Tercer Cuartil)	Mediana de la segunda mitad (9, 10, 12, 14, 30): Q3 = (12 + 14) / 2 = 13
4	Calcular IQR (Rango Intercuartílico)	IQR = Q3 - Q1 = 13 - 4 = 9
5	Calcular Límite Inferior	LI = Q1 - 1.5 * IQR = 4 - 1.5 * 9 = -9.5
6	Calcular Límite Superior	LS = Q3 + 1.5 * IQR = 13 + 1.5 * 9 = 26.5
7	Identificar Valores Atípicos	Valores fuera del rango (-9.5, 26.5): 30 es un valor atípico.

Problema 1: Dos empresas, A y B, fabrican bombillas. Se prueban muestras de bombillas de cada empresa y se registra su duración (en horas):

Empresa A: Media = 1000 horas, Desviación estándar = 50 horas

Empresa B: Media = 1000 horas, Desviación estándar = 150 horas

¿Qué empresa produce bombillas con una duración más consistente (menos variable)?
Si quieres comprar bombillas que duren *alrededor* de 1000 horas, ¿qué empresa elegirías? ¿Por qué?
Si necesitas buscar bombillas que duren mas de 1100 horas, ¿qué empresa elegirías? ¿Por qué?

Problema 2: Se registran las alturas (en cm) de los estudiantes de dos clases:

Clase 1: 160, 165, 170, 175, 180

Clase 2: 150, 160, 170, 180, 190

Calcula la media y la desviación estándar (muestral) para cada clase.
¿Qué clase tiene mayor variabilidad en las alturas?
Si se agrega un estudiante de 200 cm a la Clase 1, ¿cómo afectaría esto a la media y a la desviación estándar? ¿Y si se agrega a la Clase 2?

Clase 1 (Alturas: 160, 165, 170, 175, 180):

Media (x̄₁):
(160 + 165 + 170 + 175 + 180) / 5 = 850 / 5 = 170 cm

Desviación Estándar Muestral (s₁):
Tabla de cálculos (Media x̄₁ = 170 cm):

Altura (x_i)	Desviación (x_i - x̄₁)	Desviación al Cuadrado (x_i - x̄₁)²
160	160 - 170 = -10	(-10)² = 100
165	165 - 170 = -5	(-5)² = 25
170	170 - 170 = 0	(0)² = 0
175	175 - 170 = 5	(5)² = 25
180	180 - 170 = 10	(10)² = 100
Suma de Cuadrados:		250

Cálculo final:
Varianza muestral (s₁²) = Suma de Cuadrados / (n-1) = 250 / (5-1) = 250 / 4 = 62.5
Desviación estándar muestral (s₁) = √Varianza = √62.5 ≈ 7.91 cm

Clase 2 (Alturas: 150, 160, 170, 180, 190):

Media (x̄₂):
(150 + 160 + 170 + 180 + 190) / 5 = 850 / 5 = 170 cm

Desviación Estándar Muestral (s₂):
Tabla de cálculos (Media x̄₂ = 170 cm):

Altura (y_i)	Desviación (y_i - x̄₂)	Desviación al Cuadrado (y_i - x̄₂)²
150	150 - 170 = -20	(-20)² = 400
160	160 - 170 = -10	(-10)² = 100
170	170 - 170 = 0	(0)² = 0
180	180 - 170 = 10	(10)² = 100
190	190 - 170 = 20	(20)² = 400
Suma de Cuadrados:		1000

Cálculo final:
Varianza muestral (s₂²) = Suma de Cuadrados / (n-1) = 1000 / (5-1) = 1000 / 4 = 250
Desviación estándar muestral (s₂) = √Varianza = √250 ≈ 15.81 cm

Resumen (Parte a):
Clase 1: Media = 170 cm, s₁ ≈ 7.91 cm.
Clase 2: Media = 170 cm, s₂ ≈ 15.81 cm.

La Clase 2 tiene mayor variabilidad en las alturas.
Justificación: La desviación estándar mide la dispersión. Como s₂ (≈ 15.81 cm) es mayor que s₁ (≈ 7.91 cm), las alturas en la Clase 2 están, en promedio, más alejadas de la media (170 cm) que las de la Clase 1.

Impacto al añadir un estudiante de 200 cm:

En Clase 1:
Nuevas alturas: 160, 165, 170, 175, 180, 200 (n'=6)
Nueva Media (x̄'₁): (850 + 200) / 6 = 1050 / 6 = 175 cm. (Aumenta)
Nueva Desviación Estándar Muestral (s'₁):
Tabla de cálculos (Nueva Media x̄'₁ = 175 cm):

Altura (x'_i)	Desviación (x'_i - x̄'₁)	Desviación al Cuadrado (x'_i - x̄'₁)²
160	160 - 175 = -15	(-15)² = 225
165	165 - 175 = -10	(-10)² = 100
170	170 - 175 = -5	(-5)² = 25
175	175 - 175 = 0	(0)² = 0
180	180 - 175 = 5	(5)² = 25
200	200 - 175 = 25	(25)² = 625
Suma de Cuadrados:		1000

Cálculo final:
Nueva Varianza (s'₁²) = 1000 / (6-1) = 1000 / 5 = 200
Nueva Desviación Estándar (s'₁) = √200 ≈ 14.14 cm. (Aumenta significativamente desde ≈7.91 cm).
*(Nota: El valor 15.81 cm en la solución original para este caso parece ser un error; el cálculo correcto es ≈14.14 cm).*

En Clase 2:
Nuevas alturas: 150, 160, 170, 180, 190, 200 (n'=6)
Nueva Media (x̄'₂): (850 + 200) / 6 = 1050 / 6 = 175 cm. (Aumenta)
Nueva Desviación Estándar Muestral (s'₂):
Tabla de cálculos (Nueva Media x̄'₂ = 175 cm):

Altura (y'_i)	Desviación (y'_i - x̄'₂)	Desviación al Cuadrado (y'_i - x̄'₂)²
150	150 - 175 = -25	(-25)² = 625
160	160 - 175 = -15	(-15)² = 225
170	170 - 175 = -5	(-5)² = 25
180	180 - 175 = 5	(5)² = 25
190	190 - 175 = 15	(15)² = 225
200	200 - 175 = 25	(25)² = 625
Suma de Cuadrados:		1750

Cálculo final:
Nueva Varianza (s'₂²) = 1750 / (6-1) = 1750 / 5 = 350
Nueva Desviación Estándar (s'₂) = √350 ≈ 18.71 cm. (Aumenta, pero menos drásticamente, desde ≈15.81 cm).

Comparación del Impacto: En ambos casos, la media aumenta a 175 cm. Sin embargo, el impacto en la desviación estándar es diferente. En Clase 1, la desviación estándar aumentó mucho (de ≈7.91 a ≈14.14), casi se duplicó. En Clase 2, que ya era más variable, la desviación estándar aumentó menos (de ≈15.81 a ≈18.71). Esto ilustra que un valor atípico (el estudiante de 200 cm) tiende a incrementar más la dispersión relativa en un conjunto de datos originalmente homogéneo (Clase 1) que en uno que ya era heterogéneo (Clase 2).

Problema 1: Tiempos de Atención en un Banco

🌍 Aplicación Real

Este tipo de análisis es crucial para la gestión de servicios. Un banco podría usar estos datos para decidir si necesita contratar más personal en una sucursal, mejorar sus procesos o redistribuir a sus empleados para que los tiempos de espera sean más consistentes y bajos para los clientes.

Se realiza un estudio sobre el tiempo (en minutos) que tardan los clientes en ser atendidos en dos sucursales de un banco. Los datos se consideran una muestra.

Sucursal A:

Tiempo (min)	Frecuencia
[0 - 5)	10
[5 - 10)	15
[10 - 15)	8
[15 - 20)	5
[20 - 25)	2

Sucursal B:

Tiempo (min)	Frecuencia
[0 - 5)	5
[5 - 10)	10
[10 - 15)	15
[15 - 20)	12
[20 - 25)	8

Calcula la media y la desviación estándar para cada sucursal.
¿En qué sucursal los tiempos de atención son más consistentes? Justifica con los datos.
Si fueras un cliente, ¿en qué sucursal es más probable que tengas que esperar más de 15 minutos? Justifica.

9. problemas interpretacion con datos agrupados en intervalos

Problemas interpretacion datos agrupados

💡 ¿Cómo sé si la desviación es alta, baja o moderada?

Una forma práctica de juzgar si la desviación estándar ($s$) es grande o pequeña es compararla directamente con la media ($\bar{x}$). Aunque no es una regla estricta, la siguiente guía es muy útil para empezar a interpretar tus resultados:

Baja Variabilidad: Si la desviación estándar es menor o igual a un décimo (1/10) de la media. Esto indica que los datos son muy consistentes y están agrupados cerca del promedio.
Ejemplo: Para una media de 70 años, una desviación de hasta 7 años (el 10%) se consideraría baja.
Variabilidad Moderada: Si la desviación estándar está entre un décimo (1/10) y tres décimos (3/10) de la media.
Ejemplo: Con la misma media de 70 años, una desviación de 15 años estaría en este rango, indicando una dispersión moderada.
Alta Variabilidad: Si la desviación estándar es mayor o igual a tres décimos (3/10) de la media. Esto sugiere que los datos están muy dispersos y la media es menos representativa del conjunto.
Ejemplo: Para una media de 70 años, una desviación de 25 años (más de 21, que es el 30%) sería considerada alta.

Nota a futuro: Esta comparación es la base de un cálculo que aprenderás formalmente en otra página, llamado Coeficiente de Variación (CV), el cual estandariza esta relación en un porcentaje. Su fórmula es: \[ CV = \left( \frac{s}{|\bar{x}|} \right) \cdot 100\% \]

Nivel Datos Agrupados:

Cálculos que incluyen evaluación de los valores obtenidos en muestras

Ejemplo Guía: Análisis de Hábitos de Lectura

Contexto: Se realiza un sondeo en un club de lectura para conocer el número de páginas que sus miembros leen por semana. Se obtiene una muestra de 50 miembros.

Tareas:

Calcular la media, varianza y desviación estándar de las páginas leídas.
Interpretar si el grupo tiene hábitos de lectura consistentes o dispersos, basándose en los resultados.

Nº de Páginas Leídas	Nº de Miembros ($f_i$)
[0 - 50)	5
[50 - 100)	15
[100 - 150)	20
[150 - 200)	8
[200 - 250]	2

Resolución del Ejemplo

a) Resultados del Cálculo:

Primero, construimos la tabla completa para obtener los valores necesarios.

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[0 - 50)	25	5	125	-87	7569	37845
[50 - 100)	75	15	1125	-37	1369	20535
[100 - 150)	125	20	2500	13	169	3380
[150 - 200)	175	8	1400	63	3969	31752
[200 - 250]	225	2	450	113	12769	25538
Total		50	5600			119050

Media: $\bar{x} = \frac{5600}{50} = 112$ páginas
Varianza: $s^2 = \frac{119050}{49} \approx 2429.59$ páginas²
Desviación estándar: $s = \sqrt{2429.59} \approx 49.29$ páginas

b) Interpretación:

El número promedio de páginas leídas es 112. La desviación estándar es de aproximadamente 49 páginas, un valor considerablemente alto en comparación con la media (casi el 44% de la media). Esto nos indica que los hábitos de lectura del club son bastante dispersos y poco consistentes. Hay una gran variabilidad entre los miembros: algunos leen mucho menos que el promedio y otros mucho más.

Ejercicio 4: Tiempos de Traslado al Trabajo

Una consultora de recursos humanos estudia el tiempo de traslado (en minutos) de los empleados de una gran oficina. Se encuesta a una muestra de 100 personas.

Calcule la media, la varianza y la desviación estándar muestrales.
Al comparar la media con la desviación estándar que calculaste, ¿consideras que esto indica una alta o baja variabilidad (o consistencia) en los tiempos de traslado? Justifica tu respuesta.

Tiempo (minutos)	Nº de Empleados ($f_i$)
[0 - 15)	10
[15 - 30)	25
[30 - 45)	40
[45 - 60)	20
[60 - 75]	5

a) Resultados del Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[0 - 15)	7.5	10	75	-27.75	770.0625	7700.625
[15 - 30)	22.5	25	562.5	-12.75	162.5625	4064.0625
[30 - 45)	37.5	40	1500	2.25	5.0625	202.5
[45 - 60)	52.5	20	1050	17.25	297.5625	5951.25
[60 - 75]	67.5	5	337.5	32.25	1040.0625	5200.3125
Total		100	3525			23118.75

Media: $\bar{x} = 35.25$ minutos
Varianza: $s^2 \approx 233.52$ min²
Desviación estándar: $s \approx 15.28$ minutos

b) Interpretación:

Una desviación estándar de más de 15 minutos es bastante alta en relación con una media de 35 minutos. Esto indica una alta variabilidad en los tiempos de viaje. Significa que los tiempos no son consistentes; mientras algunos empleados tienen traslados cortos, un número importante tiene viajes muy largos. El promedio por sí solo no describe bien la situación de un empleado "típico" debido a esta alta dispersión.

Ejercicio 5: Gasto Mensual en Ocio

Se realiza una encuesta a una muestra de 60 jóvenes para conocer su gasto mensual en ocio (cine, salidas, etc.), en pesos chilenos.

Calcule la media, la varianza y la desviación estándar muestrales del gasto.
Al comparar la media con la desviación estándar, ¿qué te dice la dispersión de los datos sobre la consistencia de los hábitos de consumo del grupo? ¿Son homogéneos o heterogéneos?

Gasto (CLP)	Nº de Jóvenes ($f_i$)
[0 - 20000)	12
[20000 - 40000)	22
[40000 - 60000)	16
[60000 - 80000)	7
[80000 - 100000]	3

a) Resultados del Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[0 - 20000)	10000	12	120000	-29000	841000000	1.0092E+10
[20000 - 40000)	30000	22	660000	-9000	81000000	1.782E+9
[40000 - 60000)	50000	16	800000	11000	121000000	1.936E+9
[60000 - 80000)	70000	7	490000	31000	961000000	6.727E+9
[80000 - 100000]	90000	3	270000	51000	2601000000	7.803E+9
Total		60	2340000			2.834E+10

Media: $\bar{x} = 39000$ pesos
Varianza: $s^2 \approx 480338983$ pesos²
Desviación estándar: $s \approx 21916.64$ pesos

b) Interpretación:

La desviación estándar de casi $22.000 es muy alta en comparación con la media de $39.000 (es más de la mitad de la media). Esto indica que los hábitos de consumo son extremadamente heterogéneos. Existe una gran diferencia entre los que gastan poco y los que gastan mucho, por lo que los datos tienen una consistencia muy baja.

Ejercicio 6: Duración de Baterías de Celulares

Un sitio web de tecnología prueba la duración de la batería (en horas) de una muestra de 40 modelos de celulares nuevos bajo uso continuo.

Calcule la media, la varianza y la desviación estándar de la duración de las baterías.
Comparando la media y la desviación estándar que calculaste, ¿consideras que el rendimiento de las baterías en el mercado es consistente o disperso? Interpreta tu conclusión.

Duración (horas)	Nº de Modelos ($f_i$)
[4 - 6)	4
[6 - 8)	10
[8 - 10)	15
[10 - 12)	8
[12 - 14]	3

a) Resultados del Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$f_i(x_i - \bar{x})^2$
[4 - 6)	5	4	20	-3.8	14.44	57.76
[6 - 8)	7	10	70	-1.8	3.24	32.4
[8 - 10)	9	15	135	0.2	0.04	0.6
[10 - 12)	11	8	88	2.2	4.84	38.72
[12 - 14]	13	3	39	4.2	17.64	52.86
Total		40	352			182.34

Media: $\bar{x} = 8.8$ horas
Varianza: $s^2 \approx 4.68$ horas²
Desviación estándar: $s \approx 2.16$ horas

b) Interpretación:

La desviación estándar (2.16 horas) es relativamente pequeña en comparación con la media (8.8 horas). Esto indica que los datos tienen una dispersión moderada, lo que se traduce en un rendimiento relativamente consistente en el mercado. Aunque hay variaciones, la mayoría de los celulares no se alejan drásticamente del promedio, ofreciendo un rendimiento predecible.

Nivel 2B:

Cálculos que incluyen evaluación de los valores obtenidos en poblaciones

Ejercicio 7: Calificaciones Finales de un 4° Medio

La siguiente tabla muestra las calificaciones finales de matemática de toda la generación de 4° Medio de un liceo, compuesta por 45 estudiantes. Al ser el universo completo de alumnos, los datos corresponden a una población.

Calcule la media poblacional ($\mu$), la varianza poblacional ($\sigma^2$) y la desviación estándar poblacional ($\sigma$).
Comparando la media con la desviación estándar que calculaste, ¿el rendimiento de la generación fue homogéneo o heterogéneo? Justifique.

Calificación	Nº de Estudiantes ($f_i$)
[1.0 - 2.0)	1
[2.0 - 3.0)	3
[3.0 - 4.0)	7
[4.0 - 5.0)	15
[5.0 - 6.0)	12
[6.0 - 7.0]	7

a) Resultados del Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \mu$	$(x_i - \mu)^2$	$f_i(x_i - \mu)^2$
[1.0 - 2.0)	1.5	1	1.5	-3.22	10.3684	10.3684
[2.0 - 3.0)	2.5	3	7.5	-2.22	4.9284	14.7852
[3.0 - 4.0)	3.5	7	24.5	-1.22	1.4884	10.4188
[4.0 - 5.0)	4.5	15	67.5	-0.22	0.0484	0.726
[5.0 - 6.0)	5.5	12	66.0	0.78	0.6084	7.3008
[6.0 - 7.0]	6.5	7	45.5	1.78	3.1684	22.1788
Total		N=45	212.5			65.778

Media Poblacional: $\mu = \frac{212.5}{45} \approx 4.72$ puntos
Varianza Poblacional: $\sigma^2 = \frac{65.778}{45} \approx 1.46$ puntos²
Desviación Estándar Poblacional: $\sigma = \sqrt{1.46} \approx 1.21$ puntos

b) Interpretación:

Para interpretar, comparamos la desviación estándar con la media: $\frac{1.21}{4.72} \approx 0.256$, lo que equivale a un 25.6%. Según nuestra guía, un valor entre 10% y 30% indica una variabilidad moderada. Por lo tanto, el rendimiento de la generación no fue completamente uniforme, pero tampoco extremadamente disperso; se puede considerar un curso con un rendimiento relativamente predecible.

Ejercicio 8: Producción Diaria de Tornillos

Una máquina produce tornillos y se analiza la longitud de toda la producción de un día, que consta de 200 unidades. Se considera esta producción diaria como una población.

Calcule la media ($\mu$), la varianza poblacional ($\sigma^2$) y la desviación estándar poblacional ($\sigma$) de la longitud de los tornillos.
Para un proceso industrial, ¿consideraría que una desviación estándar como la calculada indica un nivel de precisión alto o bajo? Interprete.

Longitud (mm)	Nº de Tornillos ($f_i$)
[19.7 - 19.8)	10
[19.8 - 19.9)	40
[19.9 - 20.0)	90
[20.0 - 20.1)	50
[20.1 - 20.2]	10

a) Resultados del Cálculo:

Intervalo	$x_i$	$f_i$	$f_i \cdot x_i$	$x_i - \mu$	$(x_i - \mu)^2$	$f_i(x_i - \mu)^2$
[19.7 - 19.8)	19.75	10	197.5	-0.205	0.042025	0.42025
[19.8 - 19.9)	19.85	40	794.0	-0.105	0.011025	0.441
[19.9 - 20.0)	19.95	90	1795.5	-0.005	0.000025	0.00225
[20.0 - 20.1)	20.05	50	1002.5	0.095	0.009025	0.45125
[20.1 - 20.2]	20.15	10	201.5	0.195	0.038025	0.38025
Total		N=200	3991.0			1.695

Media Poblacional: $\mu = \frac{3991}{200} = 19.955$ mm
Varianza Poblacional: $\sigma^2 = \frac{1.695}{200} = 0.008475$ mm²
Desviación Estándar Poblacional: $\sigma = \sqrt{0.008475} \approx 0.092$ mm

b) Interpretación:

La desviación estándar ($\approx 0.092$ mm) es extremadamente pequeña en comparación con la media ($19.955$ mm). La relación es $\frac{0.092}{19.955} \approx 0.0046$, o un 0.46%. Este valor es muy inferior al 10%, lo que indica una variabilidad bajísima. Para un proceso industrial, este resultado es excelente y demuestra un alto nivel de precisión y consistencia en la producción.

10. problemas de comparacion de informacion agrupada en intervalos

fr

11. Aplicaciones y Toma de Decisiones con Medidas de Dispersión

Aplicaciones y Toma de Decisiones con Medidas de Dispersión

Repaso: Media y Desviación Estándar

La media nos da un "valor central" o "promedio" de un conjunto de datos. La desviación estándar nos indica qué tan dispersos están los datos alrededor de esa media.

Aplicaciones en Diversos Campos

1. Control de Calidad

En la fabricación de productos, la desviación estándar es crucial para asegurar que los productos cumplan con las especificaciones. Una desviación estándar baja indica que los productos son muy similares entre sí (lo cual suele ser deseable).

Ejemplo: Una fábrica de tornillos quiere que los tornillos tengan una longitud de 5 cm. Si la desviación estándar de las longitudes es muy alta, significa que hay muchos tornillos significativamente más largos o más cortos que 5 cm, lo cual es inaceptable.

2. Finanzas y Riesgo

En finanzas, la desviación estándar se usa como una medida de *riesgo* o *volatilidad*. Una inversión con una desviación estándar alta en sus rendimientos es más riesgosa (pero también tiene el potencial de mayores ganancias o pérdidas).

Ejemplo:

Acción A: Rendimiento promedio anual = 8%, Desviación estándar = 2%
Acción B: Rendimiento promedio anual = 8%, Desviación estándar = 10%

La Acción B es mucho más volátil que la Acción A. Aunque ambas tienen el mismo rendimiento promedio, los rendimientos de la Acción B varían mucho más de un año a otro.

3. Medicina y Salud

Las medidas de dispersión se usan para analizar datos de salud, como la presión arterial, el colesterol, el peso, etc. Ayudan a identificar valores atípicos (que podrían indicar una enfermedad) y a evaluar la efectividad de tratamientos.

Ejemplo: Si la desviación estándar de la presión arterial en un grupo de pacientes es muy alta, podría indicar que algunos pacientes tienen presión arterial muy alta o muy baja, lo cual requiere atención médica.

4. Educación

En educación, las medidas de dispersión ayudan a comprender la variabilidad en el rendimiento de los estudiantes. Una desviación estándar alta en las calificaciones de un examen podría indicar que el examen fue demasiado difícil o que hay grandes diferencias en el nivel de comprensión de los estudiantes.

Ejemplo: Un profesor que encuentra una alta desviación estándar en las calificaciones de un examen podría decidir revisar el material con más detalle o ajustar su método de enseñanza.

5. Deportes

En deportes, se usan para analizar el rendimiento de los atletas. Por ejemplo, la consistencia en los tiempos de un corredor o en los puntajes de un golfista se puede evaluar con la desviación estándar.

Ejemplo: Un golfista con una baja desviación estándar en sus puntajes es más consistente que un golfista con una alta desviación estándar, incluso si ambos tienen el mismo puntaje promedio.

Limitaciones de las Medidas de Dispersión

Sensibilidad a Valores Extremos: El rango y, en menor medida, la desviación estándar, pueden verse muy afectados por valores atípicos.
No Describen la Forma de la Distribución: Las medidas de dispersión no nos dicen si la distribución de los datos es simétrica, sesgada, bimodal, etc. Dos conjuntos de datos pueden tener la misma media y desviación estándar, pero tener formas muy diferentes.
Interpretación Relativa: La "importancia" de una desviación estándar depende del contexto y de la magnitud de la media. Una desviación estándar de 10 es grande si la media es 20, pero pequeña si la media es 1000. (Para esto sirve el *coeficiente de variación*, que se calcula como Desviación Estándar / Media).

Importancia del Contexto

Siempre es fundamental interpretar las medidas de dispersión *en el contexto* de los datos. No hay reglas universales para decir si una desviación estándar es "alta" o "baja". Depende de lo que se esté midiendo y de las implicaciones prácticas de la variabilidad.

Introducción a la Significancia Estadística (Concepto General)

En estadística, a menudo queremos saber si una diferencia observada entre dos grupos (por ejemplo, en sus medias o desviaciones estándar) es "real" o simplemente se debe al azar. La *significancia estadística* nos ayuda a evaluar esto.

Ejemplo (sin entrar en detalles técnicos): Si comparamos las alturas promedio de hombres y mujeres, es probable que encontremos una diferencia. La pregunta es: ¿Esta diferencia es lo suficientemente grande como para ser considerada "estadísticamente significativa", o podría deberse simplemente a la variación aleatoria dentro de cada grupo?

Nota: No vamos a entrar en cálculos de significancia estadística en esta página, pero es importante que los estudiantes sepan que este concepto existe y que es fundamental en la investigación científica.

Ejercicios y Problemas

Ejercicio 1: Imagina que eres un inversor y tienes que elegir entre dos fondos de inversión. Ambos fondos tienen un rendimiento promedio del 10% anual. El Fondo A tiene una desviación estándar del 5% y el Fondo B tiene una desviación estándar del 15%. ¿Qué fondo elegirías si:

Eres averso al riesgo (prefieres la seguridad).
Estás dispuesto a asumir más riesgo a cambio de la posibilidad de mayores ganancias.

Ejercicio 2: Un profesor califica dos exámenes. En el Examen 1, la media es 70 y la desviación estándar es 10. En el Examen 2, la media es 70 y la desviación estándar es 2. ¿Qué examen tuvo resultados más homogéneos? ¿Qué implicaciones podría tener esto para el profesor?

Problema 1: Una empresa fabrica dos tipos de baterías, A y B. Se prueban muestras de cada tipo y se mide su duración (en horas):

Batería A: Media = 40 horas, Desviación estándar = 5 horas

Batería B: Media = 50 horas, Desviación estándar = 10 horas

¿Qué tipo de batería dura más, en promedio?
¿Qué tipo de batería tiene una duración más consistente?
Si necesitas una batería que dure *al menos* 30 horas, ¿cuál elegirías? ¿Por qué?
Si necesitas una batería que dure *alrededor* de 45 horas, ¿cuál elegirías? ¿Por qué?

Problema 2: Se miden las alturas (en cm) de los jugadores de dos equipos de baloncesto:

Equipo X: 190, 192, 195, 198, 200

Equipo Y: 180, 185, 195, 205, 210

Calcula la media y la desviación estándar (muestral) para cada equipo.
¿Qué equipo tiene jugadores con alturas más similares entre sí?
Un nuevo jugador se une al Equipo X. Su altura es de 220 cm. ¿Cómo afecta esto a la media y a la desviación estándar del Equipo X?

Equipo X (Alturas: 190, 192, 195, 198, 200):

Media (x̄_X):
(190 + 192 + 195 + 198 + 200) / 5 = 975 / 5 = 195 cm

Desviación Estándar Muestral (s_X):
Tabla de cálculos (Media x̄_X = 195 cm):

Altura (x_i)	Desviación (x_i - x̄_X)	Desviación al Cuadrado (x_i - x̄_X)²
190	190 - 195 = -5	(-5)² = 25
192	192 - 195 = -3	(-3)² = 9
195	195 - 195 = 0	(0)² = 0
198	198 - 195 = 3	(3)² = 9
200	200 - 195 = 5	(5)² = 25
Suma de Cuadrados:		68

Cálculo final:
Varianza muestral (s_X²) = Suma de Cuadrados / (n-1) = 68 / (5-1) = 68 / 4 = 17
Desviación estándar muestral (s_X) = √Varianza = √17 ≈ 4.12 cm

Equipo Y (Alturas: 180, 185, 195, 205, 210):

Media (ȳ_Y):
(180 + 185 + 195 + 205 + 210) / 5 = 975 / 5 = 195 cm

Desviación Estándar Muestral (s_Y):
Tabla de cálculos (Media ȳ_Y = 195 cm):

Altura (y_i)	Desviación (y_i - ȳ_Y)	Desviación al Cuadrado (y_i - ȳ_Y)²
180	180 - 195 = -15	(-15)² = 225
185	185 - 195 = -10	(-10)² = 100
195	195 - 195 = 0	(0)² = 0
205	205 - 195 = 10	(10)² = 100
210	210 - 195 = 15	(15)² = 225
Suma de Cuadrados:		650

Cálculo final:
Varianza muestral (s_Y²) = Suma de Cuadrados / (n-1) = 650 / (5-1) = 650 / 4 = 162.5
Desviación estándar muestral (s_Y) = √Varianza = √162.5 ≈ 12.75 cm

Resumen:
Equipo X: Media = 195 cm, s_X ≈ 4.12 cm.
Equipo Y: Media = 195 cm, s_Y ≈ 12.75 cm.

El Equipo X tiene jugadores con alturas más similares entre sí.
Justificación: Su desviación estándar (s_X ≈ 4.12 cm) es menor que la del Equipo Y (s_Y ≈ 12.75 cm), indicando menor dispersión de las alturas alrededor de la media.

Impacto en el Equipo X al añadir un jugador de 220 cm:

Nuevas alturas del Equipo X: 190, 192, 195, 198, 200, 220 (Ahora n=6)

Nueva Media (x̄'_X):
(975 + 220) / 6 = 1195 / 6 ≈ 199.17 cm.
Efecto: La media aumenta (de 195 cm a ≈199.17 cm).

Nueva Desviación Estándar Muestral (s'_X):
Tabla de cálculos (Nueva Media x̄'_X ≈ 199.17 cm):

Altura (x'_i)	Desviación (x'_i - x̄'_X)	Desviación al Cuadrado (x'_i - x̄'_X)²
190	190 - 199.17 ≈ -9.17	(-9.17)² ≈ 84.09
192	192 - 199.17 ≈ -7.17	(-7.17)² ≈ 51.41
195	195 - 199.17 ≈ -4.17	(-4.17)² ≈ 17.39
198	198 - 199.17 ≈ -1.17	(-1.17)² ≈ 1.37
200	200 - 199.17 ≈ 0.83	(0.83)² ≈ 0.69
220	220 - 199.17 ≈ 20.83	(20.83)² ≈ 433.89
Suma de Cuadrados:		≈ 588.84

Cálculo final:
Nueva Varianza muestral (s'_X²) = Suma de Cuadrados / (n'-1) ≈ 588.833 / (6-1) ≈ 588.833 / 5 ≈ 117.767
Nueva Desviación estándar muestral (s'_X) = √Varianza ≈ √117.767 ≈ 10.85 cm
Efecto: La desviación estándar aumenta significativamente (de ≈4.12 cm a ≈10.85 cm).

Explicación: El nuevo jugador (220 cm) es un valor atípico. Esto eleva la media y, al estar muy alejado de ella, aumenta drásticamente la suma de las desviaciones cuadradas. Esto resulta en una varianza y desviación estándar mucho mayores, indicando que las alturas del equipo ahora son considerablemente menos homogéneas.

12. Coeficiente de Variación

Coeficiente de Variación (CV)

¿Por qué necesitamos otra medida de dispersión?

Hemos visto que la desviación estándar mide la dispersión *absoluta* de los datos alrededor de la media. Pero, ¿qué pasa si queremos comparar la variabilidad entre conjuntos de datos que tienen unidades diferentes o medias muy distintas? Ahí es donde entra en juego el Coeficiente de Variación (CV).

Definición y Fórmula

El Coeficiente de Variación (CV) es una medida de dispersión relativa. Expresa la desviación estándar como un porcentaje de la media. Esto nos permite comparar la variabilidad entre conjuntos de datos que, de otra manera, no serían comparables directamente.

Fórmula (para una muestra):

\[ \Large \color{blue}{\boxed{ CV = \frac{s}{\bar{x}} \times 100\% }} \]

Fórmula (para una población):

\[ \Large \color{blue}{\boxed{ CV = \frac{\sigma}{\mu} \times 100\% }} \]

Donde:

$CV$ es el coeficiente de variación.
$s$ es la desviación estándar muestral.
$\bar{x}$ es la media muestral (y $\bar{x} \neq 0$).
$\sigma$ es la desviación estándar poblacional.
$\mu$ es la media poblacional (y $\mu \neq 0$).

Importante: La media debe ser distinta de cero para que el CV tenga sentido. No se puede dividir por cero.

Interpretación

Sin unidades: El CV es adimensional. No tiene unidades de medida, ya que las unidades de la desviación estándar y la media se cancelan. Esto es lo que permite comparar la variabilidad entre conjuntos de datos con diferentes unidades.
Dispersión relativa: El CV nos dice qué tan grande es la desviación estándar *en relación con* la media. Un CV del 20% significa que la desviación estándar es el 20% de la media.
Valores altos vs. bajos:
- Un CV *más alto* indica *mayor* dispersión relativa.
- Un CV *más bajo* indica *menor* dispersión relativa.
No hay valores "buenos" o "malos": No existe un umbral universal para interpretar el CV como "alto" o "bajo". Depende *totalmente del contexto*. En algunos campos (como la ingeniería de precisión), un CV del 5% podría considerarse alto. En otros (como las ciencias sociales), un CV del 30% podría considerarse normal.

Ejemplos

Ejemplo 1 (Comparación con diferentes unidades):

Queremos comparar la variabilidad de la altura (en cm) y el peso (en kg) de un grupo de personas:

Alturas: Media = 170 cm, Desviación estándar = 10 cm
Pesos: Media = 70 kg, Desviación estándar = 14 kg

No podemos comparar directamente las desviaciones estándar (10 cm vs. 14 kg) porque tienen unidades diferentes. Calculamos el CV:

CV (Alturas) = (10 cm / 170 cm) * 100% ≈ 5.88%
CV (Pesos) = (14 kg / 70 kg) * 100% = 20%

Conclusión: El peso tiene una variabilidad relativa *mucho mayor* que la altura en este grupo.

Ejemplo 2 (Comparación con medias muy diferentes):

Queremos comparar la variabilidad de los ingresos en dos grupos:

Grupo A (Estudiantes): Media = $500, Desviación estándar = $100
Grupo B (Profesionales): Media = $5000, Desviación estándar = $500

Aunque la desviación estándar del Grupo B es mucho mayor en términos absolutos, calculamos el CV:

CV (Grupo A) = ($100 / $500) * 100% = 20%
CV (Grupo B) = ($500 / $5000) * 100% = 10%

Conclusión: Los ingresos del Grupo A (estudiantes) tienen una variabilidad relativa *mayor* que los del Grupo B (profesionales).

Ejercicios

Ejercicio 1: Calcula el CV para los siguientes conjuntos de datos:

Media = 60, Desviación estándar = 9
Media = 15, Desviación estándar = 3
Media = 1200, Desviación estándar = 60

Ejercicio 2: Un investigador compara la variabilidad en la duración de dos tipos de bombillas. La bombilla A tiene una duración promedio de 800 horas con una desviación estándar de 80 horas. La bombilla B tiene una duración promedio de 1200 horas con una desviación estándar de 100 horas. ¿Qué tipo de bombilla tiene mayor variabilidad relativa en su duración?

Ejercicio 3: Explica con tus propias palabras por qué el Coeficiente de Variación es útil para comparar la dispersión de conjuntos de datos que tienen diferentes unidades de medida.

13. Coeficiente de Variación con Datos en Tablas

Coeficiente de Variación (CV) con Datos en Tablas

Repaso: Coeficiente de Variación

El Coeficiente de Variación (CV) es una medida de dispersión *relativa*. Expresa la desviación estándar como un porcentaje de la media. Es útil para comparar la variabilidad entre conjuntos de datos con diferentes unidades o medias.

Fórmula: $ CV = \frac{s}{\bar{x}} \times 100\% $ (muestra) o $ CV = \frac{\sigma}{\mu} \times 100\% $ (población)

CV con Datos en Tablas

Cuando los datos están en tablas de frecuencias (simples o con intervalos), calculamos la media ($\bar{x}$) y la desviación estándar ($s$) como ya aprendimos, y luego aplicamos la fórmula del CV.

Ejemplo 1: Tabla de Frecuencias Simple

Datos: Número de hermanos de un grupo de estudiantes:

Número de Hermanos	Frecuencia (f)
0	6
1	12
2	7
3	3
Total	28

Pasos:

Calcular la media ($\bar{x}$): (Repasa la página 3 si es necesario). \[ \bar{x} = \frac{(0 \times 6) + (1 \times 12) + (2 \times 7) + (3 \times 3)}{28} = \frac{0 + 12 + 14 + 9}{28} = \frac{35}{28} = 1.25 \]
Calcular la desviación estándar (s): (Repasa las páginas 4 y 5 si es necesario). Para este ejemplo, te daremos el resultado: $s \approx 0.96$
Calcular el CV: \[ CV = \frac{s}{\bar{x}} \times 100\% = \frac{0.96}{1.25} \times 100\% \approx 76.8\% \]

Interpretación: La desviación estándar del número de hermanos es aproximadamente el 76.8% de la media. Hay una variabilidad relativa alta.

Ejemplo 2: Tabla de Frecuencias con Intervalos

Datos: Tiempos (en minutos) de espera en una fila:

Tiempo (min)	Frecuencia (f)
0 - 4	8
5 - 9	14
10 - 14	10
15 - 19	6
20 - 24	2
Total	40

(Cálculos de media y desviación estándar omitidos para brevedad, pero se asume que ya se saben calcular de páginas anteriores. Se dan los resultados directamente).

Media ($\bar{x}$) ≈ 8.75 minutos
Desviación estándar (s) ≈ 5.72 minutos

CV = (5.72 / 8.75) * 100% ≈ 65.37%

Interpretación: La desviación estándar del tiempo de espera es aproximadamente el 65.37% de la media. Hay una variabilidad relativa considerable.

Ejercicios

Ejercicio 1: La siguiente tabla muestra la distribución de puntajes en una prueba:

Puntaje	Frecuencia
50 - 59	5
60 - 69	10
70 - 79	15
80 - 89	12
90 - 99	8

Calcula la media y la desviación estándar (muestral) de los puntajes.
Calcula el coeficiente de variación.
Interpreta el resultado del CV.

Ejercicio 2: Compara la variabilidad relativa de los tiempos de atención en las dos sucursales del banco del Problema 1 de la página 5 (usando los resultados que ya calculaste).

Problema 1 Se tienen datos sobre los ingresos anuales de dos grupos de personas:

Grupo X (Trabajadores a tiempo parcial): Media = $10,000, Desviación estándar = $2,000
Grupo Y (Trabajadores a tiempo completo): Media = $40,000, Desviación estándar = $4,000

Calcula el CV para cada grupo.
¿Qué grupo tiene mayor dispersión relativa en sus ingresos?
¿Qué implicaciones prácticas podría tener esta diferencia en la variabilidad relativa?

14. Ejercicios de Selección Múltiple (Parte 1)

Ejercicios de Selección Múltiple (Parte 1)

Subunidad 1: Análisis de Datos Estadísticos con Medidas de Dispersión

Instrucciones: Elige la alternativa correcta. Haz clic en "Mostrar/Ocultar Solución" para ver la respuesta y el desarrollo.

Ejercicio 1: ¿Cuál de las siguientes variables es cualitativa nominal?

Número de hijos.
Temperatura corporal.
Marca de automóvil.
Nivel de satisfacción (bajo, medio, alto).
Años de escolaridad.

Ejercicio 2: ¿Cuál de las siguientes variables es cuantitativa continua?

Cantidad de asignaturas aprobadas.
Color de ojos.
Peso de una persona.
Tipo de sangre.
Número de calzado.

Ejercicio 3: ¿Cuál de las siguientes *no* es una medida de tendencia central?

Media.
Mediana.
Moda.
Rango.
Promedio.

Ejercicio 4: Datos: 2, 4, 6, 8, 10. Calcula la media.

6
5
4
7
8

Ejercicio 5: Datos: 1, 3, 5, 5, 7. Calcula la mediana.

3
4
5
4.2
1

Ejercicio 6: Datos: 2, 2, 4, 5, 5, 5, 6. Calcula la moda.

2
4
4.14
5
6

Ejercicio 7: Datos: 3, 7, 1, 9, 5. Calcula el rango.

3
9
6
8
5

Ejercicio 8: Datos: 2, 4, 6, 8. Calcula la varianza *muestral*.

4
5
5.33
20
16

Ejercicio 9: Datos: 2, 4, 6, 8. Calcula la desviación estándar *muestral*.

4
2
2.58
5
6.67

Ejercicio 10: Si un conjunto de datos tiene desviación estándar 0, se puede concluir:

La media es 0.
La mediana es 0.
Todos los datos son iguales entre sí.
Hay un error en el cálculo.
No hay datos.

Ejercicio 11: ¿Cuál describe mejor una distribución con alta desviación estándar?

Datos muy agrupados alrededor de la media.
Datos muy dispersos.
Datos con una mediana muy alta.
Datos con una media muy alta.
Datos con una moda muy alta.

Ejercicio 12: Tabla de frecuencias. X: 1, 2, 3, 4. f: 2, 3, 4, 1. Calcula la media.

2.5
2.4
2
3
10

Ejercicio 13: Un valor atípico es, *generalmente*:

Un error de medición.
Un dato muy cercano a la media.
Un dato muy alejado de la mayoría de los demás datos.
La mediana del conjunto de datos.
El valor más frecuente.

Ejercicio 14: Si la media de un conjunto de datos es 10 y la mediana es 12, ¿qué se puede *intuir* sobre la distribución?

Es perfectamente simétrica.
Está sesgada a la derecha.
Está sesgada a la izquierda.
No se puede intuir nada sin más información.
La desviación estándar es 2.

Ejercicio 15: ¿Cuál de las siguientes afirmaciones sobre la desviación estándar es *siempre* verdadera?

Es igual a la media.
Es mayor que la media.
Es menor que la media.
Es un valor no negativo.
Es igual al rango.

15. Ejercicios de Selección Múltiple (Parte 2)

Ejercicios de Selección Múltiple (Parte 2)

Subunidad 1: Análisis de Datos Estadísticos con Medidas de Dispersión

Ejercicio 16: Datos agrupados: Intervalo [0-9] (marca de clase 4.5, frecuencia 5); Intervalo [10-19] (marca de clase 14.5, frecuencia 10); Intervalo [20-29] (marca de clase 24.5, frecuencia 5). Calcula la media (aproximada).

14.5
15
16
15.5
14

Ejercicio 17: Con los datos del Ejercicio 16, calcula la varianza muestral (aproximada).

50
75
56.25
60.25
63.42

Ejercicio 18: Con los datos del Ejercicio 16, calcula la desviación estándar muestral (aproximada).

7.25
7.5
7
8
52.63

Ejercicio 19: Dos grupos tienen la misma media, pero el Grupo A tiene una desviación estándar mayor que el Grupo B. ¿Qué implica esto?

Los datos del Grupo A están más cerca de la media.
Los datos del Grupo A están más dispersos.
El Grupo A tiene más datos que el Grupo B.
El Grupo B tiene más datos que el Grupo A.
No se puede concluir nada sin más información.

Ejercicio 20: Grupo X: Media = 80, Desviación estándar = 5. Grupo Y: Media = 80, Desviación estándar = 12. ¿Cuál tiene mayor variabilidad *relativa*?

Grupo X.
Grupo Y.
Tienen la misma variabilidad relativa.
No se puede determinar sin el coeficiente de variación.
No se puede determinar sin los datos originales.

Ejercicio 21: Calcula el Coeficiente de Variación (CV) para un conjunto de datos con media = 25 y desviación estándar = 5.

5%
20%
25%
125%
No se puede calcular.

Ejercicio 22: ¿Para qué es *más útil* el Coeficiente de Variación?

Calcular la media.
Calcular la mediana.
Comparar dispersión entre conjuntos con diferentes unidades o medias.
Determinar si la distribución es normal.
Encontrar valores atípicos.

Ejercicio 23: Boxplot: Mediana = 50, Q1 = 40, Q3 = 60. Estima la desviación estándar (asumiendo normalidad).

10
14.8
20
7.4
No se puede estimar.

Ejercicio 24: Boxplot A: caja más ancha que Boxplot B. ¿Qué implica?

A tiene menor dispersión que B.
A tiene mayor dispersión que B.
A y B tienen igual dispersión.
A tiene mayor mediana que B.
No se puede comparar la dispersión.

Ejercicio 25: Histograma: alto y estrecho. ¿Qué implica?

Alta desviación estándar.
Baja desviación estándar.
Media alta.
Mediana alta.
No se puede inferir nada.

Ejercicio 26: Datos: 10, 12, 15, 18, 20, 25, 50. ¿Cuál es *probablemente* un valor atípico?

10
15
20
50
No hay valores atípicos.

Ejercicio 27: Datos: Q1 = 30, Q3 = 40. Un dato se considera atípico si es menor que X o mayor que Y. Calcula X e Y (regla 1.5*IQR).

X = 10, Y = 60
X = 15, Y = 55
X = 20, Y = 50
X = 25, Y=45
X=30, Y= 40

Ejercicio 28: ¿Cuál afirmación sobre valores atípicos es *falsa*?

Pueden distorsionar la media.
Pueden afectar la desviación estándar.
Siempre deben ser eliminados del conjunto de datos.
Pueden indicar errores de medición.
Pueden ser valores válidos pero inusuales.

Ejercicio 29: Dos conjuntos de datos tienen la misma desviación estándar. ¿Se puede afirmar que tienen la misma variabilidad?

Sí, siempre.
No, nunca.
Sí, si tienen la misma media.
Sí, si tienen el mismo rango.
Sí, si tienen el mismo número de datos.

Ejercicio 30: Un histograma sesgado a la izquierda, ¿qué relación tiene entre media y mediana?

Media > Mediana.
Media < Mediana.
Media = Mediana.
No se puede determinar sin los datos.
Media = 2 * Mediana.

16. test old

🏋️‍♀️ Problema: Distribución de Pesos

¿Cuál es el intervalo con la mayor frecuencia?
¿Cuántas personas pesan entre 70 kg y 80 kg?

🏋️‍♀️ Problema: Distribución de Pesos

10 frutas vendidas.

¿Cuál es el intervalo con la mayor frecuencia?
¿Cuántas personas pesan entre 70 kg y 80 kg?

🏋️‍♀️ Problema: Distribución de Pesos

Se registró el peso en kg de un grupo de personas. El siguiente histograma muestra la distribución de los datos agrupados en intervalos.

¿Cuál es el intervalo con la mayor frecuencia?
¿Cuántas personas pesan entre 70 kg y 80 kg?

🍰 Problema: Preferencia de Postres

En una encuesta sobre el postre favorito, se obtuvieron los siguientes resultados. Analiza el gráfico para responder.

¿Cuál es el postre con mayor preferencia?
¿Qué porcentaje aproximado de personas prefiere Frutas Frescas?

Diagrama de Caja y Bigotes

El siguiente diagrama muestra la distribución de las edades en una oficina.

Ojiva de Frecuencia Acumulada

La ojiva muestra el número acumulado de estudiantes según sus puntajes en un examen.

📈 Problema: Horas de Estudio vs. Calificación

Se recopilaron datos de un grupo de estudiantes para analizar si existe una relación entre las horas que dedican a estudiar para un examen y la calificación que obtienen. Observa el gráfico de dispersión.

¿Qué tipo de correlación parece existir entre las variables?
¿Hay algún punto que podría considerarse un valor atípico?

📊 Problema: Ventas Mensuales de una Tienda

El siguiente gráfico muestra la evolución de las ventas (en miles de $) de una tienda durante el primer semestre del año.

¿En qué mes se registraron las mayores ventas?
¿Cuál fue la tendencia general de las ventas durante el semestre?

Sitio:	PROFEARAUCO.CL
Curso:	Media 3
Libro:	Los datos estan dispersos?

Imprimido por:	Invitado
Día:	sábado, 6 de septiembre de 2025, 12:57

Goles (\(x_i\))	Desviación Absoluta \(\|x_i - \bar{x}\|\)
0	\|0 - 2\| = 2
1	\|1 - 2\| = 1
1	\|1 - 2\| = 1
2	\|2 - 2\| = 0
6	\|6 - 2\| = 4
Suma de Desviaciones:	8

Intervalo	\(x_i\)	\(f_i\)	\(f_i \cdot x_i\)	\(x_i - \bar{x}\)	\((x_i - \bar{x})^2\)	\(f_i(x_i - \bar{x})^2\)
50 - 59	54.5	5	272.5	-20	400	2000
60 - 69	64.5	10	645	-10	100	1000
70 - 79	74.5	15	1117.5	0	0	0
80 - 89	84.5	12	1014	10	100	1200
90 - 99	94.5	8	756	20	400	3200
Total		50	3805			7400

Los datos estan dispersos?

Tabla de contenidos

1. Recordemos cosas de la Estadística

¿Qué es la Estadística?

Tipos de Datos

✍️ Ejercicio 1: Clasificación de Datos

✍️ Ejercicio 2: Creación de Ejemplos

Medidas de Tendencia Central

🧪 Ejemplo: Media (Promedio)

🧪 Ejemplo: Mediana (Valor Central)

🧪 Ejemplo: Moda (Valor más Frecuente)

⏱️ Problema 1: El Efecto de un Valor Atípico

📚 Problema 2: Representatividad de las Medidas

2. Introducción a la Estadística y la Variabilidad

Introducción a la Variabilidad

Variabilidad o Dispersión

La Importancia de Medir la Variabilidad

1. La media sola puede ser engañosa 🤥

2. Mide la consistencia y la confiabilidad 🎯

3. Permite comparaciones justas ⚖️

4. Ayuda a identificar valores atípicos (outliers) ⚠️

✍️ Problema 1: Análisis de Distribución

🏀 Problema 2: Rendimiento de Equipos

Problema 3: Grupos de estudiantes

🟩 Grupo A

🟧 Grupo B

3. Organización de Datos en Tablas e Interpretación Gráfica

Organización de Datos en Tablas e Interpretación Gráfica

Tipos de Tablas de Frecuencias

Ejemplos de Tablas para Organizar Datos

🧪 Ejemplo: Tabla de Datos Simple

🧪 Ejemplo: Tabla de Frecuencias (Datos no Agrupados)

🧪 Ejemplo: Tabla de Frecuencias (Datos Agrupados)

Interpretación Visual de la Dispersión

Histogramas

Diagramas de Caja (Boxplots)

🧪 Ejemplo: Comparación de Boxplots

Ejercicios y Problemas

✍️ Ejercicio 1: Tabla de Frecuencias

✍️ Ejercicio 2: Datos Agrupados

✍️ Ejercicio 3: Interpretación de Histogramas

✍️ Problema 1: Comparando la Dispersión

✍️ Problema 2: Análisis de Consultorios

Consultorio A

Consultorio B

4. Organización de Datos en Tablas e Interpretación Gráfica

Organización de Datos en Tablas e Interpretación Gráfica

Importancia de la Organización de Datos

Tipos de Tablas

1. Tabla de Datos Simple (o Lista de Datos)

2. Tabla de Frecuencias

3. Tabla de Frecuencias con Datos Agrupados (Intervalos)

Preparación de Datos para el Cálculo de Medidas de Dispersión

Interpretación Visual de la Dispersión: Histogramas y Diagramas de Caja

Histogramas

📊 Similitudes:

📈 Diferencias:

🔍 Resumen de Diferencias:

🎯 Conclusión:

Ejercicios y Problemas

Explicación

5. La Desviación Media (optativo complementario): Una Medida de Dispersión Intuitiva

La Desviación Media: Una Medida de Dispersión Intuitiva

Cálculo Paso a Paso

Desviación Media vs. Desviación Estándar

Ejercicios Propuestos

6. Medidas de Dispersión: Rango, Varianza y Desviación Estándar

Medidas de Dispersión: Rango, Varianza y Desviación Estándar

Repaso: ¿Qué es la Dispersión?

El Rango

La Varianza (\(s^2\) o \(\sigma^2\))

Desviación Típica (o Estándar)

Ejercicios y Problemas Propuestos

7. Cálculo de Varianza y Desviación Estándar para Datos Agrupados

Cálculo de Varianza y Desviación Estándar para Datos Agrupados

Repaso

Cálculo Paso a Paso (Ejemplo Guiado)

Ejercicios y Problemas

Nivel 1:

Cálculos de varianza y Desviación estándar