Imprimir el Libro CompletoImprimir el Libro Completo

Capitulo 0.2 N° enteros (nivelacion)

Sitio: PROFEARAUCO.CL
Curso: Media 1
Libro: Capitulo 0.2 N° enteros (nivelacion)
Imprimido por: Invitado
Día: sábado, 6 de septiembre de 2025, 12:42

Tabla de contenidos

1. Números Enteros

Números Enteros

🤓 Definición

El conjunto de los números enteros se representa con el símbolo \( \mathbb{Z} \) y se define como la unión de los números naturales \( \mathbb{N} \), el cero (0), y los opuestos de los números naturales (los negativos).

\( \mathbb{Z} = \{..., -3, -2, -1, 0, 1, 2, 3, ...\} \)

O también, de forma más formal:

\( \mathbb{Z} = \mathbb{N} \cup \{0\} \cup \{ -n \mid n \in \mathbb{N} \} \)

Donde \( -n \) representa el opuesto aditivo de \( n \).

Los números enteros positivos son los mismos números naturales \( (1, 2, 3, ...) \), los números enteros negativos son sus opuestos \( (-1, -2, -3, ...) \) y es importante recordar que el cero no es ni positivo ni negativo.

En las próximas secciones, veremos cómo estos números se ubican en una recta numérica, cómo se comparan, y qué propiedades tienen al operar con ellos.

🌍 Números Negativos en Nuestro Día a Día

Los números negativos no son solo una idea abstracta, ¡están por todas partes! Los usamos para representar deudas, faltantes o movimientos en sentido contrario.

  • 🌡️ Temperatura: Una temperatura de -5°C indica que estamos 5 grados Celsius por debajo del punto de congelación del agua (0°C).
  • 💰 Dinero: Si debes $10.000, puedes representar esa deuda como -$10.000.
  • 🗺️ Altitud: El Mar Muerto se encuentra a -430 metros, es decir, 430 metros bajo el nivel del mar (0 metros).
  • ↕️ Movimiento: En un ascensor, si estás en el piso 1 y bajas 2 pisos hasta el subterráneo, hiciste un movimiento de -2 pisos.

En la recta numérica, los números negativos se ubican a la izquierda del cero, como un espejo de los positivos.

Recta numérica con números enteros

Propiedades de los Números Enteros

📐 1. Clausura (o Cerradura)

La suma, resta y multiplicación de dos números enteros siempre da como resultado otro número entero. El conjunto \( \mathbb{Z} \) es "cerrado" para estas operaciones.

Si \( a, b \in \mathbb{Z} \), entonces:

  • \( a + b \in \mathbb{Z} \)
  • \( a - b \in \mathbb{Z} \)
  • \( a \cdot b \in \mathbb{Z} \)

Ejemplo: \( 5 + (-3) = 2 \), \( 7 - 10 = -3 \), \( 4 \cdot (-2) = -8 \). Todos los resultados son enteros.

Ejercicios de Clausura:

  1. \( -8 + 5 \)
  2. \( 12 - 15 \)
  3. \( -6 \cdot 3 \)
  4. \( -4 + (-7) \)

📐 2. Asociatividad

Al sumar o multiplicar tres o más enteros, no importa cómo los agrupes, el resultado será el mismo.

Si \( a, b, c \in \mathbb{Z} \), entonces:

  • \( (a + b) + c = a + (b + c) \)
  • \( (a \cdot b) \cdot c = a \cdot (b \cdot c) \)

Ejemplo: \( (2 + 3) + (-1) = 5 - 1 = 4 \), que es lo mismo que \( 2 + (3 + (-1)) = 2 + 2 = 4 \).

Comprueba la Asociatividad:

  1. Calcula \( (-5 + 2) + 7 \) y luego \( -5 + (2 + 7) \).
  2. Calcula \( (3 \cdot -2) \cdot 4 \) y luego \( 3 \cdot (-2 \cdot 4) \).
  3. Calcula \( (-1 + (-4)) + 6 \) y luego \( -1 + (-4 + 6) \).

💡 3. Conmutatividad

¡El orden de los factores no altera el producto! Y en este caso, tampoco altera la suma. Puedes cambiar el orden de los números al sumar o multiplicar y el resultado no cambiará.

Si \( a, b \in \mathbb{Z} \), entonces:

  • \( a + b = b + a \)
  • \( a \cdot b = b \cdot a \)

Ejemplo: \( -5 + 7 = 2 \), que es lo mismo que \( 7 + (-5) = 2 \).

Comprueba la Conmutatividad:

  1. ¿Es \( -9 + 4 \) igual a \( 4 + (-9) \)?
  2. ¿Es \( -2 \cdot 6 \) igual a \( 6 \cdot (-2) \)?
  3. ¿Es \( 0 + (-3) \) igual a \( -3 + 0 \)?

🤓 4. Existencia del Elemento Neutro

Hay números que, al operar con ellos, no alteran al otro número.

  • El 0 es el neutro aditivo: cualquier entero sumado con 0 queda igual. \( a + 0 = a \)
  • El 1 es el neutro multiplicativo: cualquier entero multiplicado por 1 queda igual. \( a \cdot 1 = a \)

Ejemplo: \( 9 + 0 = 9 \) y \( -6 \cdot 1 = -6 \).

Aplica el Elemento Neutro:

  1. \( -15 + 0 \)
  2. \( 7 \cdot 1 \)
  3. \( 0 + 23 \)
  4. \( -8 \cdot 1 \)

🤓 5. Existencia del Elemento Opuesto (o Inverso Aditivo)

Para cada número entero \( a \), siempre existe otro entero \( -a \) (su opuesto) que, al sumarlos, el resultado es 0 (el neutro aditivo).

Para todo \( a \in \mathbb{Z} \), existe \( (-a) \in \mathbb{Z} \) tal que \( a + (-a) = 0 \).

Ejemplo: El opuesto de 5 es -5, porque \( 5 + (-5) = 0 \). El opuesto de -3 es 3, porque \( -3 + 3 = 0 \).

Encuentra el Elemento Opuesto:

  1. ¿Qué número sumado a 12 da 0?
  2. ¿Qué número sumado a -9 da 0?
  3. \( ? + 7 = 0 \)
  4. \( ? + (-4) = 0 \)

⚠️ ¡Cuidado! No existe el inverso multiplicativo para todos los enteros.

Si bien existe un inverso aditivo para cada entero, no ocurre lo mismo con la multiplicación. Por ejemplo, para el número 5, no existe un número entero que al multiplicarlo por 5 dé como resultado 1 (el neutro multiplicativo). El número sería \( \frac{1}{5} \), pero \( \frac{1}{5} \) no es un número entero. Esta es la razón por la que la división no es una operación cerrada en \( \mathbb{Z} \).

📐 6. Distributividad

Esta propiedad conecta la multiplicación con la suma. La multiplicación "se distribuye" sobre la suma.

Si \( a, b, c \in \mathbb{Z} \), entonces:

\( a \cdot (b + c) = (a \cdot b) + (a \cdot c) \)

Ejemplo: \( 2 \cdot (3 + (-1)) = 2 \cdot 2 = 4 \), que es lo mismo que \( (2 \cdot 3) + (2 \cdot (-1)) = 6 - 2 = 4 \).

Comprueba la Distributividad:

  1. Calcula \( -3 \cdot (4 + 2) \) y luego \( (-3 \cdot 4) + (-3 \cdot 2) \).
  2. Calcula \( (5 + (-2)) \cdot 3 \) y luego \( (5 \cdot 3) + (-2 \cdot 3) \).
  3. Calcula \( 4 \cdot (-1 + 6) \) y luego \( (4 \cdot -1) + (4 \cdot 6) \).

2. Construcción de los Números Enteros a partir de los Naturales (complemento)

Construcción de los Números Enteros a partir de los Naturales

🌍 ¿Por qué construir algo que ya conocemos?

Aunque usamos los números negativos y el cero todos los días, en matemática es crucial tener una base sólida y sin contradicciones. La construcción formal de los números enteros (\(\mathbb{Z}\)) a partir de los naturales (\(\mathbb{N}\)) nos permite definir rigurosamente qué es un número negativo y cómo opera, usando solo las reglas que ya conocemos de los números naturales. Es como construir un rascacielos: necesitamos cimientos lógicos y bien definidos.

📐 Definición Matemática Formal

Los números enteros se construyen formalmente mediante los siguientes pasos:

  1. Conjunto Base: Partimos del producto cartesiano de los números naturales consigo mismos, \(\mathbb{N} \times \mathbb{N}\). Este conjunto está formado por todos los pares ordenados \((a, b)\) donde \(a\) y \(b\) son números naturales. \[ \mathbb{P} = \{(a, b) \mid a, b \in \mathbb{N}\} \]
  2. Relación de Equivalencia: Definimos una relación \(\sim\) sobre este conjunto de pares. Decimos que dos pares son equivalentes si representan la misma "diferencia". \[ (a, b) \sim (c, d) \iff a + d = b + c \]
  3. Clases de Equivalencia: Cada conjunto de pares que son equivalentes entre sí forma una "clase de equivalencia". Cada una de estas clases es un número entero. \[ \mathbb{Z} = \{ [(a, b)] \mid (a, b) \in \mathbb{P} \} \]

Por lo tanto, el conjunto de los números enteros \(\mathbb{Z}\) es, formalmente, el conjunto cociente de \(\mathbb{N} \times \mathbb{N}\) bajo la relación \(\sim\).

💡 La Idea Clave: La resta escondida

La intuición detrás del par \((a, b)\) es que representa la resta \(a - b\). Como la resta no siempre es posible en los números naturales, usamos este par para "codificar" la idea de una resta sin salirnos del conjunto \(\mathbb{N}\).

  • El par \((5, 2)\) representa la idea de \(5-2\), es decir, el entero \(+3\).
  • El par \((2, 5)\) representa la idea de \(2-5\), es decir, el entero \(-3\).
  • El par \((4, 4)\) representa la idea de \(4-4\), es decir, el entero \(0\).

La relación \(a + d = b + c\) es simplemente una forma de decir que \(a - b = c - d\) sin usar el signo de resta.

🤓 Explicación Detallada de las Clases de Equivalencia

Cada número entero es una familia infinita de pares ordenados. La diferencia entre los componentes del par determina a qué familia pertenece:

  • Si \(a > b\), la clase \([(a, b)]\) representa un entero positivo (ej: \([(3, 1)]\) representa al \(+2\)).
  • Si \(a < b\), la clase \([(a, b)]\) representa un entero negativo (ej: \([(1, 3)]\) representa al \(-2\)).
  • Si \(a = b\), la clase \([(a, b)]\) representa al cero (ej: \([(2, 2)]\) representa al \(0\)).

Aunque hay infinitas formas de escribir el mismo número entero, la relación de equivalencia las une. Por ejemplo, todos los siguientes pares pertenecen a la misma clase (el entero +2): \[ [(3, 1)] = [(5, 3)] = [(100, 98)] \] Todos ellos son tratados como un único objeto matemático: el número 2.

⚠️ ¡No es un punto ni una fracción!

Es muy importante no confundir la notación. El par \((a, b)\) en este contexto no representa un punto en el plano cartesiano ni la fracción \(a/b\). Es una construcción específica para definir los números enteros.

📐 Definición de Operaciones en \(\mathbb{Z}\)

La suma y el producto de enteros se definen a partir de sus representantes como pares ordenados:

  • Suma: \[ [(a, b)] + [(c, d)] = [(a + c, b + d)] \]
  • Producto: \[ [(a, b)] \cdot [(c, d)] = [(ac + bd, ad + bc)] \]

Estas definiciones son consistentes, lo que significa que no importa qué par elijas de la clase de equivalencia, el resultado siempre pertenecerá a la misma clase de equivalencia final.

Ejemplo Numérico: Suma

Sumemos \(+2\) y \(+2\). Usaremos los representantes \([(3, 1)]\) para el primer \(+2\) y \([(4, 2)]\) para el segundo.

Definición: \( [(3, 1)] + [(4, 2)] = [(3 + 4, 1 + 2)] \)

Cálculo: \( = [(7, 3)] \)

Interpretación: La clase \([(7, 3)]\) representa el entero \(7 - 3 = 4\). Efectivamente, \(2 + 2 = 4\).

Ejemplo Numérico: Producto

Calculemos el producto de \(+2\) y \(-2\). Usaremos los representantes \([(3, 1)]\) para \(+2\) y \([(1, 3)]\) para \(-2\).

Definición: \( [(3, 1)] \cdot [(1, 3)] = [(3 \cdot 1 + 1 \cdot 3, 3 \cdot 3 + 1 \cdot 1)] \)

Cálculo: \( = [(3 + 3, 9 + 1)] = [(6, 10)] \)

Interpretación: La clase \([(6, 10)]\) representa el entero \(6 - 10 = -4\). Efectivamente, \(2 \cdot (-2) = -4\).

🤓 Conclusión

Esta construcción formal, aunque abstracta, es la que permite extender los números naturales (\(\mathbb{N}\)) al conjunto de los enteros (\(\mathbb{Z}\)) de una manera lógica y consistente. Nos asegura que los números negativos y el cero se comportan exactamente como esperamos, siguiendo reglas que se derivan directamente de la aritmética de los números naturales. Es un ejemplo perfecto de la elegancia y el rigor del pensamiento matemático.

3. Números Enteros: Orden y Recta Numérica

Números Enteros: Orden y Recta Numérica

🤓 La Recta Numérica

La recta numérica es una línea recta que se extiende infinitamente en ambas direcciones y nos sirve como un mapa para visualizar y ordenar todos los números enteros.

📐 ¿Cómo la construimos?

  1. Dibujamos una línea recta horizontal.
  2. Marcamos un punto en el centro que será nuestro origen o punto de referencia: el cero (0).
  3. A la derecha del cero, a distancias iguales, ubicamos los enteros positivos: 1, 2, 3, 4, ...
  4. A la izquierda del cero, con la misma separación, ubicamos los enteros negativos: -1, -2, -3, -4, ...

Recta numérica mostrando números enteros negativos y positivos

💡 La Regla de Oro del Orden

  • Un número es mayor que otro si está más a la derecha en la recta numérica.
  • Un número es menor que otro si está más a la izquierda.

Orden en los Números Enteros

La recta numérica nos permite comparar fácilmente dos números enteros. Usamos los siguientes símbolos:

  • < : Menor que
  • > : Mayor que
  • = : Igual a
  • ≤ : Menor o igual que
  • ≥ : Mayor o igual que

Ejemplos de Comparación

  • 2 < 5 (2 es menor que 5) porque 2 está a la izquierda de 5.
  • -3 > -7 (-3 es mayor que -7) porque -3 está a la derecha de -7.
  • 0 > -2 (0 es mayor que -2) porque 0 está a la derecha de -2.
  • -1 < 4 (-1 es menor que 4) porque -1 está a la izquierda de 4.

Ejercicio 1: Completa mentalmente con <, > o = según corresponda y luego comprueba tu respuesta.

  1. -4 ___ 2
  2. 0 ___ -6
  3. -1 ___ -1
  4. -10 ___ -1
  5. 5 ___ 1
  6. 7 ___ 7

Ejercicio 2: Ordena los siguientes números de menor a mayor, visualizándolos en la recta numérica: { -3, 5, 0, -2, 4, -6}

Ejercicio 3: Escribe tres números enteros que sean menores que -2.

Ejercicio 4: Escribe tres números enteros que sean mayores que -5 y menores que 3.

🤓 Número Opuesto

Cada número entero tiene un opuesto, que es el mismo número con signo contrario.

Están a igual distancia del cero, pero en sentidos opuestos sobre la recta numérica.

Se dice que dos números son opuestos porque al sumarlos el resultado es cero, el neutro aditivo.

  • El opuesto de \( 3 \) es \( -3 \) porque \( 3 + (-3) = 0 \)
  • El opuesto de \( -8 \) es \( 8 \) porque \( -8 + 8 = 0 \)
  • El opuesto de \( 0 \) es el mismo \( 0 \) porque \( 0 + 0 = 0 \)

🧠 Comprensión del Número Opuesto:

  1. ¿Cuál es el opuesto de \( -15 \)?
  2. ¿Cuál es el opuesto de \( 12 \)?
  3. ¿Cuál es el opuesto de \( 0 \)?
  4. ¿Cuál es el opuesto de \( -1 \)?
  5. ¿Cuál es el opuesto de \( -999 \)?
  6. ¿Cuál es el opuesto de \( x \)?
  7. ¿Cuál es el opuesto de \( -a \)?

💡 ¿Sabías que...?

El opuesto del opuesto de un número es el mismo número: \( -(-a) = a \).

¡Es como volver al mismo lugar después de dar dos pasos hacia atrás en la recta numérica!

🔄 Opuesto del Opuesto:

  1. \( -(-3) = \ ? \)
  2. \( -(-10) = \ ? \)
  3. \( -(-0) = \ ? \)
  4. \( -(-7) = \ ? \)
  5. \( -(-(-2)) = \ ? \)
  6. \( -(-x) = \ ? \)
  7. \( -(-(-a)) = \ ? \)

Valor Absoluto

🤓 El valor absoluto de un número entero es su distancia al cero en la recta numérica. Como es una distancia, siempre es un valor positivo o cero.

Se representa encerrando el número entre dos barras verticales: | |.

  • |5| = 5 (La distancia de 5 al 0 es 5 unidades).
  • |-3| = 3 (La distancia de -3 al 0 es 3 unidades).
  • |0| = 0 (La distancia de 0 a sí mismo es 0).

Ejercicio 5: Calcula el valor absoluto de los siguientes números.

  1. |-8|
  2. |7|
  3. |-1|
  4. |0|
  5. |15|
  6. |-10|

⚠️ ¡Cuidado! No confundas el tamaño con el valor.

Un error común es pensar que un número negativo "grande" como -8 es mayor que un número como 2. ¡Es al revés! Aunque |-8| (que es 8) es más grande que |2| (que es 2), el número -8 está mucho más a la izquierda en la recta, por lo tanto, -8 es menor que 2.

Es fundamental insistir en esta diferencia:

  • Mayor/Menor: Se refiere exclusivamente al orden en la recta numérica. Un número a la derecha es siempre mayor.
  • "Más Grande" / "Más Pequeño": Son términos ambiguos que la gente suele asociar con el valor absoluto o la distancia al cero.

🌍 Piensa en deudas: ¿Qué prefieres, deber $2 (una situación de -2) o deber $8 (una situación de -8)? Es mejor deber $2. Por lo tanto, la situación -2 es "mejor" o mayor que la situación -8.

4. Operaciones con Números Enteros: Suma y Resta

Operaciones con Números Enteros: Suma y Resta

🌍 Entendiendo los Números Enteros con Dinero

Imagina que el dinero que tienes en tu bolsillo son números positivos y el dinero que debes son números negativos. Esta es una forma simple de ver cómo funcionan:

  • Si tienes $5 y recibes $3 más: \(5 + 3 = 8\). Ahora tienes $8.
  • Si debes $4 y pides prestado $2 más: \((-4) + (-2) = -6\). Ahora tu deuda total es de $6.
  • Si debes $7 pero solo tienes $5: \((-7) + 5 = -2\). Después de pagar, todavía debes $2.
  • Si tienes $8 y pagas una deuda de $3: \(8 + (-3) = 5\). Después de pagar, te quedan $5.

Suma de Números Enteros

📐 Reglas para Sumar Enteros

1. Números con el mismo signo: Se suman sus valores y se mantiene el mismo signo.

  • \(3 + 5 = 8\)
  • \((-4) + (-2) = -6\)

2. Números con distinto signo: Se restan sus valores (el mayor menos el menor) y el resultado se queda con el signo del número que tiene mayor valor.

  • \(7 + (-2) = 5\) (El 7 es más grande, el resultado es positivo)
  • \((-8) + 3 = -5\) (El 8 es más grande, el resultado es negativo)

🤓 Visualizando la Suma en la Recta Numérica

Usar la recta numérica es una excelente estrategia visual para entender cómo se comportan los números enteros. La regla de oro es:

  • Sumar un número positivo significa moverse hacia la derecha (en la dirección de los números más grandes).
  • Sumar un número negativo significa moverse hacia la izquierda (en la dirección de los números más pequeños).

Veamos los cuatro casos posibles:

Caso 1: Positivo + Positivo (Ejemplo: \(3 + 2\))

Partimos del 3 y, como sumamos un número positivo (2), nos movemos 2 unidades a la derecha. ¡Llegamos al 5!

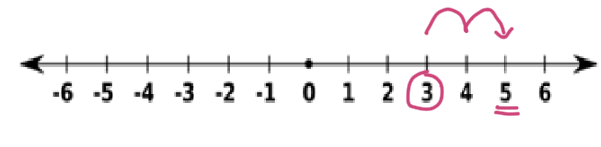
Suma de 3 + 2 en la recta numérica

Caso 2: Negativo + Negativo (Ejemplo: \((-4) + (-1)\))

Partimos del -4 y, como sumamos un número negativo (-1), nos movemos 1 unidad a la izquierda. ¡Llegamos al -5!

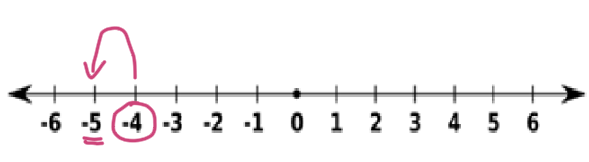
Suma de -4 + (-1) en la recta numérica

Caso 3: Positivo + Negativo (Ejemplo: \(5 + (-3)\))

Partimos del 5 y, como sumamos un número negativo (-3), nos movemos 3 unidades a la izquierda. ¡Llegamos al 2!

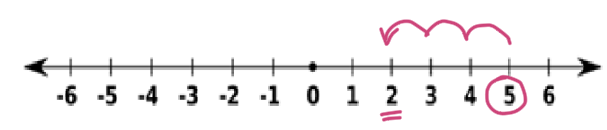
Suma de 5 + (-3) en la recta numérica

Caso 4: Negativo + Positivo (Ejemplo: \((-2) + 6\))

Partimos del -2 y, como sumamos un número positivo (6), nos movemos 6 unidades a la derecha. ¡Llegamos al 4!

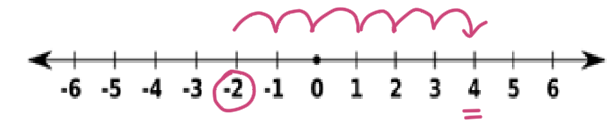
Suma de -2 + 6 en la recta numérica

Resta de Números Enteros

💡 Idea Clave: Transformar la Resta en Suma

Restar un número entero es exactamente lo mismo que sumar su número opuesto. Este truco simplifica todas las restas.

Por ejemplo: \(5 - 3\) se convierte en \(5 + (-3)\).

⚠️ ¡Advertencia! Cuidado al restar un negativo

Este es un error muy común. Restar un número negativo es sumar su opuesto positivo. ¡Los dos signos "menos" seguidos se convierten en un "más"!

Ejemplo: \(4 - (-1)\) se transforma en \(4 + 1 = 5\).

Ejemplo: Restar es lo mismo que sumar el opuesto

Esta es una regla fundamental. En vez de pensar en restar, siempre puedes transformarlo en una suma, lo que a menudo es más fácil. Simplemente sumas el número opuesto.

Observa los siguientes casos:

  • \( 5 - 3 \) se convierte en \( 5 + (-3) = 2 \)
  • \( -2 - 6 \) se convierte en \( -2 + (-6) = -8 \)
  • \( 4 - (-1) \) se convierte en \( 4 + 1 = 5 \)
  • \( -7 - (-3) \) se convierte en \( -7 + 3 = -4 \)
💡 Estrategias para Operaciones Combinadas

Cuando te enfrentas a una cadena de sumas y restas, existen dos métodos muy efectivos para llegar al resultado. ¡Puedes elegir el que más te acomode!

  • Método 1 (Directo): Operar de izquierda a derecha, paso a paso.
  • Método 2 (Agrupar): Juntar todos los números positivos, luego todos los negativos, y al final resolver la operación entre ambos grupos.
Ejemplo 1: Resolviendo \( 2 + (-5) - (-3) + 1 - 4 \)

Paso 1: Convertir todas las restas en sumas del opuesto.
La expresión se transforma en: \( 2 + (-5) + 3 + 1 + (-4) \)

Paso 2 (Método Directo):
\( 2 + (-5) = -3 \)
\( -3 + 3 = 0 \)
\( 0 + 1 = 1 \)
\( 1 + (-4) = -3 \)

Paso 2 (Método de Agrupar):
Positivos: \( 2 + 3 + 1 = 6 \)
Negativos: \( (-5) + (-4) = -9 \)
Resultado: \( 6 + (-9) = -3 \)

Resultado Final: -3

Ejemplo 2: Resolviendo \( -6 - 2 + (-1) - (-7) + 4 \)

Paso 1: Convertir todas las restas en sumas del opuesto.
La expresión se transforma en: \( -6 + (-2) + (-1) + 7 + 4 \)

Paso 2 (Método Directo):
\( -6 + (-2) = -8 \)
\( -8 + (-1) = -9 \)
\( -9 + 7 = -2 \)
\( -2 + 4 = 2 \)

Paso 2 (Método de Agrupar):
Positivos: \( 7 + 4 = 11 \)
Negativos: \( (-6) + (-2) + (-1) = -9 \)
Resultado: \( 11 + (-9) = 2 \)

Resultado Final: 2

📝 Práctica Guiada: Suma y Resta de Enteros

Estos ejercicios están organizados en 5 niveles. Resuelve cada nivel y luego presiona su respectivo botón para ver las soluciones.

Nivel 1: Suma de Números Positivos

  1. \( (+7) + (+3) = \)
  2. \( (+9) + (+8) = \)
  3. \( (+2) + (+6) + (+4) = \)
  4. \( (+5) + (+1) + (+9) = \)
  5. \( 11 + 4 = \)
  6. \( 15 + 8 = \)
  7. \( 20 + 12 = \)
  8. \( 3 + 6 + 9 = \)
  9. \( 10 + 20 + 5 = \)
  10. \( 7 + 2 + 11 = \)

Nivel 2: Suma de Números Negativos

  1. \( (-5) + (-4) = \)
  2. \( (-8) + (-6) = \)
  3. \( (-10) + (-2) = \)
  4. \( (-15) + (-5) = \)
  5. \( (-1) + (-9) = \)
  6. \( (-2) + (-3) + (-4) = \)
  7. \( (-7) + (-1) + (-2) = \)
  8. \( (-5) + (-5) + (-5) = \)
  9. \( (-10) + (-20) + (-30) = \)
  10. \( (-8) + (-2) + (-10) = \)

Nivel 3: Suma con Signos Mixtos

  1. \( 12 + (-5) = \)
  2. \( 8 + (-10) = \)
  3. \( 20 + (-25) = \)
  4. \( (-7) + 3 = \)
  5. \( (-15) + 20 = \)
  6. \( (-9) + 9 = \)
  7. \( 6 + (-10) + 2 = \)
  8. \( (-8) + 12 + (-3) = \)
  9. \( 20 + (-5) + (-15) = \)
  10. \( -3 + 13 + (-10) = \)

Nivel 4: Resta de Números Enteros

Recuerda la idea clave: restar un número es lo mismo que sumar su opuesto.

  1. \( 20 - 8 = \)
  2. \( 10 - 17 = \)
  3. \( 30 - (+10) = \)
  4. \( -15 - 5 = \)
  5. \( -9 - 11 = \)
  6. \( (-7) - (+8) = \)
  7. \( 14 - (-6) = \)
  8. \( 10 - (-10) = \)
  9. \( 5 - (-15) = \)
  10. \( (-8) - (-5) = \)
  11. \( (-12) - (-20) = \)
  12. \( (-9) - (-9) = \)

Nivel 5: Operaciones Combinadas

Usa la estrategia que más te acomode: operar de izquierda a derecha o agrupar.

  1. \( 8 - 10 + 3 = \)
  2. \( -5 - 4 + 12 = \)
  3. \( 10 + (-5) - 6 = \)
  4. \( 15 - 20 + 5 - 1 = \)
  5. \( -7 - 3 + 10 - 2 = \)
  6. \( 20 - (-10) - 5 = \)
  7. \( -8 - (-4) + (-5) = \)
  8. \( 14 - 9 - (-2) + 1 = \)
  9. \( -3 + (-7) - (-10) + 1 = \)
  10. \( 30 - 40 + (-5) - (-15) = \)

Encuentra el Sumando Faltante

1. \(4 + \_\_\_ = 1\)

2. \(\_\_\_ + (-3) = -8\)

3. \(-2 + \_\_\_ = 5\)

4. \(\_\_\_ + 7 = 0\)

5. \(-9 + \_\_\_ = -4\)

6. \(\_\_\_ + (-1) = -1\)

Problemas con Números Enteros

1. La temperatura en la mañana era de -3°C. Al mediodía, la temperatura subió 8°C. Por la noche, bajó 5°C. ¿Cuál fue la temperatura al final del día?

2. Un submarino se encuentra a -120 metros (120 metros bajo el nivel del mar). Primero, asciende 40 metros. Luego, desciende 65 metros. ¿A qué profundidad se encuentra el submarino finalmente?

3. Ana tenía $50 en su cuenta bancaria. Hizo un retiro de $80, luego depositó $35 y finalmente hizo otro retiro de $20. ¿Cuál es el saldo de su cuenta?

4. En un juego, Juan avanzó 5 pasos, retrocedió 9 pasos, luego avanzó 3 pasos y finalmente retrocedió 2 pasos. ¿Cuál es su posición final respecto al punto de inicio?

5. Un ascensor se encuentra en el piso 3. Sube 5 pisos, luego baja 9 pisos, sube 2 pisos y finalmente baja 6 pisos. ¿En qué piso se encuentra el ascensor al final?

¡Practica con estos ejercicios y verás cómo dominas la suma y la resta de números enteros!

5. Problemas de Variación con Números Enteros

Problemas de Variación con Números Enteros

En este tipo de problemas, nos interesa encontrar la diferencia entre dos valores. Esta diferencia nos muestra cómo ha cambiado una cantidad, ya sea aumentando (variación positiva) o disminuyendo (variación negativa).

📐 Fórmula Clave de Variación

Para encontrar la diferencia o variación entre dos números enteros, siempre usamos la misma fórmula:

Variación = Valor Final - Valor Inicial

  • Un resultado positivo indica un aumento o incremento.
  • Un resultado negativo indica una disminución o decremento.

Ejemplos Resueltos

1. Variación de Temperatura

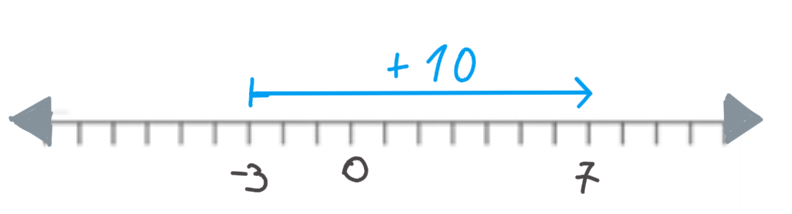
Problema: La temperatura a las 8:00 AM era de -3°C y a las 12:00 PM era de 7°C. ¿Cuál fue la variación de temperatura?

  • Valor final: 7°C
  • Valor inicial: -3°C

Operación: \( 7 - (-3) = 7 + 3 = 10 \)
Respuesta: La variación de temperatura fue de 10°C (un aumento de 10°C).

Termómetro mostrando variación de -3 a 7 grados

2. Cambio de Altitud

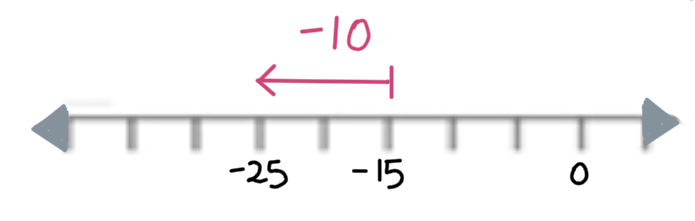
Problema: Un buzo se encontraba a -15 metros y descendió hasta -25 metros. ¿Cuál fue la variación en su altitud?

  • Valor final: -25 m
  • Valor inicial: -15 m

Operación: \( -25 - (-15) = -25 + 15 = -10 \)
Respuesta: La variación en su altitud fue de -10 metros (un descenso de 10 metros).

Buzo descendiendo de -15 a -25 metros

3. Diferencia de Dinero

Problema: Ana tenía $12 en su cuenta y luego de una transacción, su saldo quedó en -$5 (debe $5). ¿Cuál fue la variación en su saldo?

  • Valor final: -$5
  • Valor inicial: $12

Operación: \( -5 - 12 = -17 \)
Respuesta: La variación en el saldo fue de -$17 (una disminución de $17).

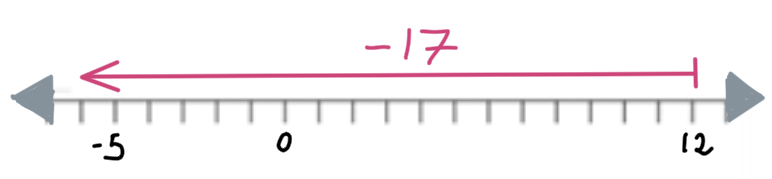
Variación de dinero de 12 a -5

4. Cambio de Posición

Problema: Un objeto se mueve desde la posición -4 en una recta numérica hasta la posición 3. ¿Cuál fue la variación en su posición?

  • Valor final: 3
  • Valor inicial: -4

Operación: \( 3 - (-4) = 3 + 4 = 7 \)
Respuesta: La variación en su posición fue de 7 (un desplazamiento de 7 unidades a la derecha).

Movimiento en recta numérica de -4 a 3

⚠️ ¡Cuidado! "Diferencia" no es lo mismo que "Variación"

En el lenguaje común, a veces usamos la palabra "diferencia" para referirnos a qué tan lejos están dos números, sin importar el orden. Sin embargo, en matemática y ciencias, la variación es un concepto preciso que nos indica tanto la magnitud como la dirección del cambio.

Por ejemplo, si la temperatura baja de 8°C a 2°C:

  • Alguien podría decir que la "diferencia" es de 6°C. Este número es correcto en magnitud, pero no nos dice si la temperatura subió o bajó.
  • La variación se calcula siempre como Valor Final - Valor Inicial. En este caso, es \( 2 - 8 = -6°C \). El signo negativo es fundamental, ya que nos confirma que la temperatura disminuyó.

Para estos problemas, ¡recuerda siempre usar la fórmula de variación para obtener la historia completa!

Ejercicios de Práctica

  1. La temperatura en la mañana era de 2°C y en la tarde era de -1°C. ¿Cuál fue la variación de temperatura?
  2. Un submarino estaba a -180 metros y ascendió a -120 metros. ¿Cuál fue la variación en su profundidad?
  3. Juan tenía una deuda de $25 (-$25) y luego de hacer un pago, su deuda quedó en $10 (-$10). ¿Cuál fue la variación en su saldo?
  4. Un ascensor estaba en el piso 8 y bajó al piso -1 (primer sótano). ¿Cuál fue la variación en su posición?
  5. En un juego, un jugador tenía -7 puntos y luego obtuvo 15 puntos. ¿Cuál fue la variación en su puntaje?
  6. Un auto se mueve de la posición 5 a la posición -2 en una carretera recta. ¿Cuál fue la variación en su posición?
  7. La temperatura al inicio de un experimento era de -5°C y al final era de -12°C. ¿Cuál fue la variación de temperatura?

6. Operaciones con Números Enteros: Multiplicación

Operaciones con Números Enteros: Multiplicación

🤓 Entendiendo la Regla de los Signos: ¿Por qué "menos por menos" es "más"?

Seguramente has aprendido las reglas de memoria, pero entender de dónde vienen te ayudará a no olvidarlas. Aquí te presentamos algunas ideas intuitivas.

Positivo × Positivo = Positivo
Es el caso más simple. Tener 3 grupos de 4 elementos te da 12 elementos. \(3 \times 4 = 12\).

Positivo × Negativo = Negativo
Piensa en esto como "añadir deudas". Si adquieres 3 deudas de $4 cada una, ahora tienes una deuda total de $12. \(3 \times (-4) = -12\).

Negativo × Negativo = Positivo
Este es el más curioso. Una forma de entenderlo es pensar que multiplicar por un negativo significa "hacer lo opuesto". Si "lo opuesto de añadir una deuda" es "quitar una deuda", ¡tu dinero aumenta!

Ejemplo: Un amigo te perdona 3 deudas de $4. Tu situación mejora en $12. \((-3) \times (-4) = 12\).

💡 Prueba con un Patrón Numérico

Observa la secuencia. Para que el patrón se mantenga, el resultado debe seguir aumentando de 2 en 2.

\( 2 \times (-2) = -4 \)
\( 1 \times (-2) = -2 \)
\( 0 \times (-2) = 0 \)
\( (-1) \times (-2) = 2 \)
\( (-2) \times (-2) = 4 \)

📐 Reglas Formales de la Multiplicación
  • Si los signos son iguales (Pos × Pos o Neg × Neg), el resultado es POSITIVO.
  • Si los signos son distintos (Pos × Neg o Neg × Pos), el resultado es NEGATIVO.
  • Cualquier número multiplicado por cero es siempre CERO.
Ejemplos: Números con el mismo signo

Cuando los dos números que multiplicas tienen el mismo signo (ambos positivos o ambos negativos), el resultado siempre será positivo.

  • Positivo × Positivo: \( 4 \times 6 = 24 \)
  • Negativo × Negativo: \( (-5) \times (-3) = 15 \)
Ejemplos: Números con distinto signo

Cuando los dos números que multiplicas tienen signos diferentes (uno positivo y otro negativo), el resultado siempre será negativo.

  • Positivo × Negativo: \( 7 \times (-2) = -14 \)
  • Negativo × Positivo: \( (-8) \times 3 = -24 \)
Ejemplos: Multiplicación por cero

Cualquier número entero, sin importar si es positivo o negativo, que se multiplica por cero, da como resultado cero.

  • \( 9 \times 0 = 0 \)
  • \( (-5) \times 0 = 0 \)
  • \( 0 \times 0 = 0 \)

En resumen

Signo Factor 1 Signo Factor 2 Signo Resultado
+ + +
- - +
+ - -
- + -
💡 Atajo para Multiplicar Varios Números

Cuando multiplicas una larga cadena de números, no necesitas ir de dos en dos. Simplemente cuenta cuántos factores negativos hay:

  • Si la cantidad de factores negativos es PAR (0, 2, 4, ...), el resultado final será POSITIVO.
  • Si la cantidad de factores negativos es IMPAR (1, 3, 5, ...), el resultado final será NEGATIVO.
Ejemplos: Multiplicación de Varios Factores

Al multiplicar varios números, el signo del resultado final depende de cuántos factores negativos hay:

  • \( 2 \times (-3) \times 4 = -24 \)

    (Hay 1 factor negativo, que es un número impar, por lo que el resultado es negativo).

  • \( (-1) \times (-5) \times 2 = 10 \)

    (Hay 2 factores negativos, un número par, por lo que el resultado es positivo).

  • \( (-2) \times (-3) \times (-4) = -24 \)

    (Hay 3 factores negativos, un número impar, por lo que el resultado es negativo).

  • \( (-1) \times 2 \times (-3) \times 4 = 24 \)

    (Hay 2 factores negativos, un número par, por lo que el resultado es positivo).

Problemas Resueltos

Ejemplo 1: Descenso de Temperatura

Problema: Si la temperatura baja 2°C cada hora, ¿cuál será el cambio total de temperatura después de 4 horas?

  • Cambio por hora: -2°C
  • Número de horas: 4

Operación: \( (-2) \times 4 = -8 \)
Respuesta: La temperatura habrá bajado 8°C en total.

Ejemplo 2: Deuda Acumulada

Problema: Juan le debe $5 a cada uno de sus 3 amigos. ¿Cuánto dinero debe en total?

  • Deuda por amigo: -$5
  • Número de amigos: 3

Operación: \( (-5) \times 3 = -15 \)
Respuesta: Juan debe $15 en total.

Ejercicios de Práctica

Cálculos Básicos: Multiplicación con dos factores

  1. \( 8 \times 5 = \)
  2. \( 7 \times 9 = \)
  3. \( 12 \times 4 = \)
  4. \( 6 \times (-7) = \)
  5. \( 10 \times (-3) = \)
  6. \( 5 \times (-11) = \)
  7. \( (-9) \times 4 = \)
  8. \( (-6) \times 8 = \)
  9. \( (-12) \times 2 = \)
  10. \( (-7) \times (-5) = \)
  11. \( (-10) \times (-10) = \)
  12. \( (-4) \times (-9) = \)

Cálculos Básicos: Multiplicación con varios factores

  1. \( 2 \times (-3) \times 5 = \)
  2. \( (-4) \times 6 \times 2 = \)
  3. \( (-1) \times (-2) \times (-3) = \)
  4. \( 7 \times (-2) \times (-1) \times (-2) = \)
  5. \( (-5) \times (-4) \times 2 = \)
  6. \( 3 \times (-3) \times (-6) = \)
  7. \( (-2) \times 5 \times (-3) \times 2 = \)
  8. \( (-1) \times (-1) \times (-2) \times (-5) = \)

Encuentra el Factor Faltante

  1. \( 4 \times \_\_\_ = -12 \)
  2. \( \_\_\_ \times (-5) = 20 \)
  3. \( -7 \times \_\_\_ = -14 \)
  4. \( \_\_\_ \times 8 = -32 \)
  5. \( -2 \times \_\_\_ \times 3 = 18 \)
  6. \( -5 \times (-2) \times \_\_\_ = -40 \)

Resolución de Problemas

  1. Un submarino desciende 30 metros por minuto. Si comienza en la superficie (0 metros), ¿a qué profundidad estará después de 5 minutos?
  2. Una empresa pierde $100 por cada hora que no produce. Si la producción estuvo detenida durante 8 horas, ¿cuál fue la pérdida total?
  3. En un juego, un jugador pierde 4 puntos por cada error que comete. Si comete 6 errores, ¿cuál será su puntaje final si partió en 0?
  4. Si la temperatura baja 3°C cada hora y la temperatura actual es de 5°C, ¿cuál será la temperatura después de 6 horas?
  5. Un buzo se encuentra a -12 metros y desciende a una velocidad de 2 metros por segundo durante 7 segundos. ¿A qué profundidad final estará?

7. Operaciones con Números Enteros: División

Operaciones con Números Enteros: División

💡 Idea Clave: La División es la Inversa de la Multiplicación

La forma más fácil de entender la división de enteros es recordar que es la operación opuesta a la multiplicación. Cada operación de multiplicación nos entrega dos operaciones de división.

Por ejemplo, si sabemos que \( 5 \times 3 = 15 \), entonces también sabemos que:

  • \( 15 \div 3 = 5 \)
  • \( 15 \div 5 = 3 \)

Usaremos esta idea para entender la regla de los signos.

🤓 Deduciendo la Regla de los Signos

Como ya dominas la multiplicación, podemos usarla para derivar las reglas de la división fácilmente:

Para cada caso, nos preguntamos: "¿Por qué número debo multiplicar el divisor para obtener el dividendo?"

Caso 1: Positivo ÷ Positivo

Razonamiento (basado en la multiplicación) Conclusión (Regla de División)
Para resolver \(12 \div 4 = ?\), nos preguntamos:
\(4 \times ? = 12\).
La única respuesta posible es 3.		 \( (+) \div (+) = (+) \)

Caso 2: Negativo ÷ Positivo

Razonamiento (basado en la multiplicación) Conclusión (Regla de División)
Para resolver \((-12) \div 4 = ?\), nos preguntamos:
\(4 \times ? = -12\).
Para obtener un resultado negativo, la respuesta debe ser negativa: -3.		 \( (-) \div (+) = (-) \)

Caso 3: Positivo ÷ Negativo

Razonamiento (basado en la multiplicación) Conclusión (Regla de División)
Para resolver \(12 \div (-4) = ?\), nos preguntamos:
\((-4) \times ? = 12\).
Para obtener un resultado positivo, la respuesta debe ser negativa: -3.		 \( (+) \div (-) = (-) \)

Caso 4: Negativo ÷ Negativo

Razonamiento (basado en la multiplicación) Conclusión (Regla de División)
Para resolver \((-12) \div (-4) = ?\), nos preguntamos:
\((-4) \times ? = -12\).
Para obtener un resultado negativo, la respuesta debe ser positiva: 3.		 \( (-) \div (-) = (+) \)

¡Como puedes ver, la regla de los signos para la división es idéntica a la de la multiplicación!

📐 Resumen: Regla de los Signos para la División
  • Si los signos son IGUALES (Pos ÷ Pos o Neg ÷ Neg), el resultado es POSITIVO.
  • Si los signos son DISTINTOS (Pos ÷ Neg o Neg ÷ Pos), el resultado es NEGATIVO.
⚠️ ¡Cuidado con el Cero en la División!

Este es un punto muy importante y una regla que no se puede romper.

  • Cero dividido por cualquier número: El resultado es siempre 0. (Ej: \( 0 \div (-5) = 0 \))
  • Un número dividido por cero: ¡Esta operación NO ESTÁ DEFINIDA en matemática! Nunca se puede dividir por cero. (Ej: \( 8 \div 0 = \text{Indefinido} \))
⚠️ ¡Cuidado! La Ambiguëdad de las Divisiones Múltiples

A diferencia de la suma o multiplicación, la división no es "asociativa". Esto significa que una expresión como \( 8 \div 4 \div 2 \) es ambigua porque el resultado cambia según el orden en que la resuelvas:

  • Agrupando por la izquierda: \( (8 \div 4) \div 2 = 2 \div 2 = 1 \)
  • Agrupando por la derecha: \( 8 \div (4 \div 2) = 8 \div 2 = 4 \)

Para evitar esta confusión, la regla matemática estándar es operar siempre de izquierda a derecha cuando hay operaciones de la misma prioridad. Por lo tanto, la interpretación correcta por defecto es la primera: el resultado es 1.

Recomendación de buena costumbre: Para ser absolutamente claro y no dejar lugar a dudas, la mejor práctica es siempre usar paréntesis. Un problema bien escrito indicará explícitamente \( (8 \div 4) \div 2 \) o \( 8 \div (4 \div 2) \) para que no haya confusión alguna.

🤓 Una Mirada Profunda: ¿Por qué la regla es "de Izquierda a Derecha"?

Es una excelente pregunta. La regla de "izquierda a derecha" no es un capricho, sino que se basa en una propiedad matemática más profunda que verás en detalle más adelante: los inversos multiplicativos (las fracciones).

En realidad, cada división se puede reescribir como una multiplicación por una fracción. Así, la operación:

\( 8 \div 4 \div 2 \)

Es matemáticamente equivalente a:

\( 8 \times \frac{1}{4} \times \frac{1}{2} \)

Y como la multiplicación sí se puede realizar en cualquier orden (es asociativa), el resultado siempre será 1, sin importar cómo la agrupes.

Pero Para no adelantarnos, por ahora nos quedamos con la regla que es más simple y nunca falla: para operaciones de la misma jerarquía, se resuelve de izquierda a derecha.

Problemas Resueltos

Ejemplo 1: Repartir una Deuda

Problema: Cuatro amigos tienen una deuda de $28 y quieren repartirla en partes iguales. ¿Cuánto dinero debe pagar cada uno?

Análisis: Una deuda se representa con un número negativo (-$28) y se reparte entre 4 personas.

Operación: \( (-28) \div 4 = -7 \)
Respuesta: Cada amigo debe $7.

Ejemplo 2: Temperatura Promedio

Problema: Durante 5 días se registraron las temperaturas: -2°C, -4°C, 1°C, -3°C y 0°C. ¿Cuál fue la temperatura promedio?

Análisis: Para el promedio, primero sumamos todas las temperaturas y luego dividimos por la cantidad de días.

Suma: \( (-2) + (-4) + 1 + (-3) + 0 = -8 \)
Operación: \( (-8) \div 5 = -1.6 \)
Respuesta: La temperatura promedio fue de -1.6°C.

Ejercicios de Práctica

Cálculos Básicos

  1. \( (-20) \div 4 = \)
  2. \( 18 \div (-2) = \)
  3. \( (-30) \div (-5) = \)
  4. \( 24 \div 8 = \)
  5. \( (-10) \div 1 = \)
  6. \( 0 \div (-9) = \)
  7. \( (-16) \div (-4) = \)
  8. \( 35 \div (-7) = \)

Encuentra el Valor Faltante

  1. \( -20 \div \_\_\_ = 5 \)
  2. \( \_\_\_ \div (-3) = 6 \)
  3. \( -14 \div \_\_\_ = -2 \)
  4. \( \_\_\_ \div 7 = -4 \)

Resolución de Problemas

  1. Un submarino se encuentra a -150 metros y desciende a velocidad constante hasta -450 metros en 6 minutos. ¿Cuál fue la variación total y cuántos metros descendió por minuto?
  2. Seis amigos tienen que pagar una deuda total de $90. Si la deuda se reparte en partes iguales, ¿cuánto debe pagar cada uno?
  3. En un experimento, la temperatura de una sustancia disminuyó 24°C en 3 horas. Si la disminución fue constante, ¿cuál fue la variación por hora?
  4. Un jugador perdió 36 puntos en 4 rondas de un juego. Si perdió la misma cantidad en cada ronda, ¿cuántos puntos perdió por ronda?

8. Potencias de Números Enteros

Potencias de Números Enteros

Ahora ampliaremos nuestro estudio a las potencias de números enteros, lo que incluye bases negativas.

🤓 Analizando el Signo con la base (-1)

La base más simple para entender qué pasa con el signo es (-1). Si observas el patrón, te darás cuenta de que el signo del resultado depende directamente de si el exponente es par o impar.

\( (-1)^1 = -1 \) (Impar → Negativo)
\( (-1)^2 = 1 \) (Par → Positivo)
\( (-1)^3 = -1 \) (Impar → Negativo)
\( (-1)^4 = 1 \) (Par → Positivo)

Este comportamiento se aplica a cualquier potencia con base negativa.

📐 Regla para Potencias de Base Negativa

Cuando la base de una potencia es un número negativo, el signo del resultado final depende del exponente:

  • Si el exponente es PAR (2, 4, 6, ...), el resultado será siempre POSITIVO.
  • Si el exponente es IMPAR (1, 3, 5, ...), el resultado será siempre NEGATIVO.
Ejemplos: Potencias de Base Negativa

Veamos cómo se aplica la regla con una base de (-2):

  • \( (-2)^2 \): El exponente (2) es par, por lo tanto el resultado es positivo. \( (-2) \times (-2) = 4 \).
  • \( (-2)^3 \): El exponente (3) es impar, por lo tanto el resultado es negativo. \( (-2) \times (-2) \times (-2) = -8 \).
  • \( (-2)^4 \): El exponente (4) es par, el resultado es positivo. \( (-2)^4 = 16 \).
  • \( (-2)^5 \): El exponente (5) es impar, el resultado es negativo. \( (-2)^5 = -32 \).
⚠️ ¡CUIDADO! No es lo mismo \( (-a)^n \) que \( -a^n \)

Los paréntesis lo cambian todo. Esta es la diferencia más importante que debes recordar. Observa el contraste directo en esta tabla:

Con Paréntesis (la base es negativa) Sin Paréntesis (la base es positiva)
\( (-3)^2 = (-3) \times (-3) = 9 \) \( -3^2 = -(3 \times 3) = -9 \)
\( (-5)^2 = (-5) \times (-5) = 25 \) \( -5^2 = -(5 \times 5) = -25 \)

Análisis detallado:

  • Con paréntesis \( (-2)^4 \): La base que se repite es -2. Multiplicas el -2 por sí mismo 4 veces.
    \( (-2) \times (-2) \times (-2) \times (-2) = 16 \) (El resultado es positivo porque el exponente es par).
  • Sin paréntesis \( -2^4 \): La base que se repite es solo el 2. El signo negativo está fuera, esperando el resultado de la potencia.
    \( -(2 \times 2 \times 2 \times 2) = -(16) = -16 \).
💡 Una Mirada Profunda: ¿Por qué funciona la regla?

Podemos descomponer una potencia de base negativa. Por ejemplo, \( (-a)^n \) es lo mismo que \( (-1)^n \times a^n \). Como \(a^n\) siempre será positivo (si a es positivo), el signo final de la operación depende exclusivamente del valor de \( (-1)^n \).

Ejercicios de Práctica

Cálculos Directos

  1. \( (-4)^2 \)
  2. \( (-2)^5 \)
  3. \( (-1)^7 \)
  4. \( (-5)^3 \)
  5. \( (-3)^4 \)
  6. \( -10^2 \) <-- ¡Ojo, sin paréntesis!
  7. \( (-6)^3 \)
  8. \( -3^3 \)
  9. \( (-1)^{20} \)
  10. \( -7^2 \)
  11. \( (-10)^3 \)
  12. \( -1^{100} \)
  13. \( (-5)^4 \)
  14. \( -2^6 \)

Encontrar el Exponente y Simplificar

  1. Si \( (-2)^x = -8 \), ¿cuánto vale \(x\)?
  2. Si \( (-3)^x = 81 \), ¿cuánto vale \(x\)?
  3. Simplifica \( (-a)^8 \)
  4. Simplifica \( (-a)^9 \)
  5. Simplifica \( (-2a)^3 \)
  6. Simplifica \( (-1)^x \), donde \(x\) es un número par.

Resolución de Problemas

  1. La temperatura en una ciudad es de -3°C. Durante la noche, esta temperatura se eleva a la tercera potencia. ¿Cuál es la temperatura final?
  2. En un juego, cada vez que pierdes, tu puntaje se multiplica por -2. Si inicias con 5 puntos y pierdes 3 veces seguidas, ¿cuál es tu puntaje final?
  3. Si \( (-2)^x = 16 \) y \( (-2)^y = -32 \), ¿cuáles son los valores de \(x\) e \(y\)?

9. Potencias de Base Entera y Exponente Entero

Potencias de Base Entera y Exponente Entero

En esta página, exploraremos las potencias donde la base es un número entero (positivo, negativo o cero) y el exponente también es un número entero (positivo, negativo o cero). Nos enfocaremos especialmente en el caso de los exponentes negativos.

🤓 Descubriendo el Patrón con Exponentes Decrecientes

La mejor forma de entender los exponentes negativos es observar el patrón que surge al disminuir sucesivamente el exponente. Usemos una tabla con base 2 para ver qué sucede.

Potencia Resultado Desarrollo (Verificación) Fracción en Potencia
\(2^3\) 8 \(2 \times 2 \times 2\) -
\(2^2\) 4 \(2 \times 2\) -
\(2^1\) 2 \(2\) -
\(2^0\) 1 \(\frac{2}{2}\) -
\(2^{-1}\) \(\frac{1}{2}\) \(\frac{1}{2}\) \(\frac{1}{2^1}\)
\(2^{-2}\) \(\frac{1}{4}\) \(\frac{1}{2} \times \frac{1}{2}\) \(\frac{1}{2^2}\)
\(2^{-3}\) \(\frac{1}{8}\) \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\) \(\frac{1}{2^3}\)

Análisis del Patrón:

  • Cada vez que el exponente disminuye en 1, el resultado se divide por la base (2).
  • Este patrón nos lleva de forma natural a que \(2^0 = 1\).
  • Al continuar el patrón, \(2^{-1}\) es simplemente \(1 \div 2\), es decir, \(\frac{1}{2}\).
  • La última columna revela la regla: un exponente negativo es lo mismo que el inverso de la base elevada al exponente positivo.
📐 Definición de Exponente Negativo

Una potencia con exponente negativo es igual al inverso multiplicativo (o recíproco) de la base elevada al exponente positivo correspondiente.

\( a^{-n} = \frac{1}{a^n} \)

(Siempre que \(a \neq 0\))

En resumen: Un exponente negativo no significa que el resultado sea negativo. Significa que debes "invertir" la base.

Ejemplo: ¿Y si la base también es negativa?

Ahora, apliquemos la misma lógica a una base negativa como (-3). Aquí se combinan dos reglas: la del exponente negativo (invertir) y la de la potencia de base negativa (el signo depende de si el exponente es par o impar).

Potencia Resultado Desarrollo (Verificación) Fracción en Potencia
\((-3)^2\) 9 \((-3) \times (-3)\) -
\((-3)^1\) -3 \((-3)\) -
\((-3)^0\) 1 \(\frac{-3}{-3}\) -
\((-3)^{-1}\) \(-\frac{1}{3}\) \(-\frac{1}{3}\) \(\frac{1}{(-3)^1}\)
\((-3)^{-2}\) \(\frac{1}{9}\) \(-\frac{1}{3} \times -\frac{1}{3}\) \(\frac{1}{(-3)^2}\)
\((-3)^{-3}\) \(-\frac{1}{27}\) \(-\frac{1}{3} \times -\frac{1}{3} \times -\frac{1}{3}\) \(\frac{1}{(-3)^3}\)

Análisis del Patrón:

  • La regla del inverso (\( a^{-n} = \frac{1}{a^n} \)) sigue funcionando perfectamente. Por ejemplo, \((-3)^{-2} = \frac{1}{(-3)^2}\).
  • Luego, resolvemos la potencia del denominador: \((-3)^2 = 9\).
  • Así, el resultado final es \(\frac{1}{9}\). Fíjate que el resultado es positivo porque el exponente (-2) actúa sobre el denominador como un exponente par.
💡 En Resumen: Cómo Resolver Potencias con Exponente Negativo

Para resolver cualquier potencia con exponente negativo, sigue estos dos pasos:

  1. Invierte la base: Reescribe la potencia como una fracción con un 1 en el numerador y la potencia con el exponente positivo en el denominador.
  2. Resuelve la nueva potencia: Calcula la potencia en el denominador, recordando las reglas de signo para bases negativas (exponente par o impar).
  • \(5^{-2} = \frac{1}{5^2} = \frac{1}{25}\)
  • \((-2)^{-3} = \frac{1}{(-2)^3} = \frac{1}{-8} = -\frac{1}{8}\) (Exponente impar → resultado negativo)
  • \((-3)^{-4} = \frac{1}{(-3)^4} = \frac{1}{81}\) (Exponente par → resultado positivo)

Ejercicios de Práctica

1. Cálculos con Bases Enteras

Aplica la regla principal: \( a^{-n} = \frac{1}{a^n} \). ¡No olvides las reglas de signo para la base!

  1. \(4^{-2}\)
  2. \(2^{-5}\)
  3. \(7^{-1}\)
  4. \((-5)^{-2}\)
  5. \((-2)^{-3}\)
  6. \(10^{-3}\)
  7. \(6^{-3}\)
  8. \((-1)^{-7}\)

2. Encontrar el Valor Faltante (Ecuaciones)

  1. Si \(2^{-x} = \frac{1}{16}\), ¿cuánto vale \(x\)?
  2. Si \(a^{-3} = \frac{1}{27}\), ¿cuánto vale \(a\)?
  3. Si \(3^{-x} = \frac{1}{81}\), ¿cuánto vale \(x\)?
  4. Si \(a^{-2} = \frac{1}{49}\), ¿cuánto vale \(a\)?
  5. Si \(5^{-x} = \frac{1}{125}\), ¿cuánto vale \(x\)?
  6. Si \(x^{-4} = \frac{1}{16}\), ¿cuánto vale \(x\)?

3. Problemas de Aplicación

  1. Una población de bacterias se reduce a la mitad cada hora. Si inicialmente hay \(2^4\) bacterias, ¿qué fracción de la población inicial quedará después de 3 horas? (Expresa la respuesta como una potencia de 2).
  2. Si la velocidad de un objeto es \(5^{-1}\) metros por segundo, ¿qué fracción de un metro recorre en un segundo?
  3. La intensidad de la luz disminuye con el cuadrado de la distancia. Si a 1 metro la intensidad es 1, ¿cómo se expresaría la intensidad a 4 metros usando una potencia con exponente negativo?

10. Propiedades de las Potencias base entera y exponente entero

Propiedades de las Potencias

Ahora que ya comprendes las potencias de base entera y exponente entero, repasaremos las propiedades fundamentales que nos ayudan a simplificar y resolver operaciones con ellas.

💡 Mapa de la Lección: Las 7 Propiedades Clave

A continuación, exploraremos 7 propiedades fundamentales de las potencias que te permitirán simplificar casi cualquier expresión. Esta tabla te servirá como un resumen y formulario de referencia rápida.

Propiedad Fórmula
1. Producto de Potencias de Igual Base \( a^m \times a^n = a^{m+n} \)
2. Cociente de Potencias de Igual Base \( \frac{a^m}{a^n} = a^{m-n} \)
3. Potencia de una Potencia \( (a^m)^n = a^{m \times n} \)
4. Potencia de Exponente Cero \( a^0 = 1 \)
5. Potencia de Exponente Uno \( a^1 = a \)
6. Potencia de un Producto \( (a \times b)^n = a^n \times b^n \)
7. Potencia de un Cociente \( (\frac{a}{b})^n = \frac{a^n}{b^n} \)

1. Producto de Potencias de Igual Base

📐 Fórmula: \(a^m \times a^n = a^{m+n}\)

Cuando se multiplican potencias con la misma base, se mantiene la base y se suman los exponentes.

Ejemplo: \( (-2)^3 \times (-2)^2 = (-2)^{3+2} = (-2)^5 = -32 \)

Ejercicios:

  1. \( (-3)^2 \times (-3)^2 \)
  2. \( 5^2 \times 5^3 \)
  3. \( 2^5 \times 2^{-3} \)
  4. \( (-4)^{-1} \times (-4)^{-2} \)
  5. \( 10^3 \times 10^{-5} \times 10^4 \)
  6. \( 7^{-4} \times 7^2 \)
  7. \( (-5)^3 \times (-5)^{-5} \)
  8. \( x^7 \cdot x^2 \)
  9. \( y^{-3} \cdot y^8 \)
  10. \( (3b)^4 \cdot (3b)^{-2} \)
  11. \( (-3a)^2 \times (-3a)^5 \)

2. Cociente de Potencias de Igual Base

📐 Fórmula: \(a^m \div a^n = a^{m-n}\) (donde \(a \neq 0\))

Cuando se dividen potencias con la misma base, se mantiene la base y se restan los exponentes.

Ejemplo: \( (-3)^5 \div (-3)^2 = (-3)^{5-2} = (-3)^3 = -27 \)

⚠️ ¡Ojo al Restar un Exponente Negativo!

Recuerda la regla de los signos. Un error común es olvidar que restar un negativo es lo mismo que sumar. Por ejemplo: \( 5^{4 - (-2)} = 5^{4+2} = 5^6 \).

Ejercicios:

  1. \( (-4)^8 \div (-4)^6 \)
  2. \( 10^7 \div 10^3 \)
  3. \( 5^2 \div 5^{-1} \)
  4. \( (-2)^{-5} \div (-2)^{-2} \)
  5. \( 7^{-3} \div 7^2 \)
  6. \( 8^{-3} \div 8^{-4} \)
  7. \( (-6)^2 \div (-6)^5 \)
  8. \( \frac{x^9}{x^3} \)
  9. \( \frac{a^3}{a^5} \)
  10. \( y^4 \div y^{-3} \)
  11. \( (-2b)^7 \div (-2b)^3 \)

3. Potencia de una Potencia

📐 Fórmula: \((a^m)^n = a^{m \times n}\)

Cuando una potencia se eleva a otro exponente, se mantiene la base y se multiplican los exponentes.

Ejemplo: \( ((-2)^3)^2 = (-2)^{3 \times 2} = (-2)^6 = 64 \)

Ejercicios:

  1. \( ((-1)^5)^3 \)
  2. \( (4^2)^3 \)
  3. \( (2^{-2})^4 \)
  4. \( ((-3)^3)^{-1} \)
  5. \( (5^{-2})^{-2} \)
  6. \( ((-2)^{-3})^{-2} \)
  7. \( (7^3)^{-2} \)
  8. \( (x^5)^2 \)
  9. \( (a^{-3})^4 \)
  10. \( ((2y)^2)^3 \)
  11. \( ((-4x^2)^3)^2 \)

4. Potencia de Exponente 0

📐 Fórmula: \(a^0 = 1\) (si \(a \neq 0\))

Cualquier número (excepto 0) elevado a la potencia 0 es igual a 1.

Ejemplo: \( (-5)^0 = 1 \)

💡 ¿De dónde viene esta regla?

Imagina que divides una potencia por sí misma. Usando la propiedad del cociente, obtienes exponente cero. Pero como sabes, cualquier cosa dividida por sí misma es 1.

\( \frac{a^n}{a^n} = a^{n-n} = a^0 \). Y también, \( \frac{a^n}{a^n} = 1 \). ¡Por eso, \(a^0 = 1\)!

Ejercicios:

  1. \( (-8)^0 \)
  2. \( 12^0 \)
  3. \( -5^0 \) (¡Ojo, sin paréntesis!)
  4. \( (3^4)^0 \)
  5. \( (-2)^5 \times (-2)^{-5} \)
  6. \( x^4 \div x^4 \) (si \(x \neq 0\))

5. Potencia de Exponente 1

📐 Fórmula: \(a^1 = a\)

Cualquier número elevado a la potencia 1 es igual a sí mismo.

Ejemplo: \( (-7)^1 = -7 \)

Ejercicios:

  1. \( (-15)^1 \)
  2. \( 20^1 \)
  3. \( (-3)^4 \div (-3)^3 \)
  4. \( 10^{-2} \times 10^3 \)
  5. \( (x^5)^1 \)
  6. \( (ab^2)^1 \)

6. Potencia de un Producto

📐 Fórmula: \((a \times b)^n = a^n \times b^n\)

La potencia de un producto es igual al producto de las potencias de cada factor.

Ejemplo: \( (-2 \times 3)^2 = (-2)^2 \times 3^2 = 4 \times 9 = 36 \)

Ejercicios (Aplicación Directa)

Aplica la propiedad para reescribir cada potencia como un producto de potencias con bases positivas.

  1. \( (-6)^2 \)
  2. \( (-10)^3 \)
  3. \( (-15)^2 \)
  4. \( (-2x)^4 \)
  5. \( (-3ab)^3 \)
  6. \( (-14)^2 \)
  7. \( (-20)^3 \)
  8. \( (-5y)^4 \)
  9. \( (-yz)^7 \)
  10. \( (-100)^2 \)
💡 Pensando al Revés: Descomponiendo una Potencia

Así como podemos "repartir" un exponente en una multiplicación, también podemos hacer lo contrario: agrupar dos potencias con el mismo exponente en una sola.

Por ejemplo: \( (-2)^2 \times (-5)^2 \) puede agruparse como \( ((-2) \times (-5))^2 = (10)^2 = 100 \). En los siguientes ejercicios, harás este proceso a la inversa.

Ejercicios (Descomposición)

Expresa cada número como unacociente de dos potencias con al menos una de las bases negativa y el mismo exponente.

  1. \(36\)
  2. \(100\)
  3. \(64\)
  4. \(225\)
  5. \(49\)
  6. \(-27\)
  7. \(-125\)
  8. \(144\)

6. Potencia de un Cociente

Ejercicios (Aplicación Directa)

Aplica la propiedad para reescribir cada potencia como un cociente de potencias con bases positivas.

  1. \( (\frac{-10}{5})^3 \)
  2. \( (\frac{12}{-4})^2 \)
  3. \( (\frac{-9}{3})^3 \)
  4. \( (\frac{-2x}{y})^4 \)
  5. \( (\frac{a}{-2b})^3 \)
  6. \( (\frac{15}{-3})^3 \)
  7. \( (\frac{-20}{-10})^2 \)
  8. \( (\frac{x}{-y})^5 \)
  9. \( (\frac{-a}{-b})^6 \)
  10. \( (\frac{4x}{-2y})^3 \)
💡 Pensando al Revés: Descomponiendo un Cociente

También podemos expresar un número como un cociente de potencias con el mismo exponente. Por ejemplo, \( 9 \) puede verse como \( 81 \div 9 \), lo que nos permite escribirlo como \( \frac{(-9)^2}{(-3)^2} \).

Ejercicios (Descomposición)

Expresa cada número como un cociente de dos potencias con al menos una de las bases negativa y el mismo exponente.

  1. \(4\)
  2. \(25\)
  3. \(8\)
  4. \(9\)
  5. \(16\)
  6. \(100\)
  7. \(-27\)
  8. \(-32\)

🏆 Desafío Final: Propiedades Combinadas

¡Es hora de poner todo en práctica! En los siguientes ejercicios, necesitarás aplicar dos o más propiedades de las potencias para llegar a la expresión más simple.

  1. Simplifica: \( (x^2 \cdot x^3)^2 \)
  2. Simplifica: \( \frac{(a^5)^2}{a^3} \)
  3. Simplifica: \( ((-2)^3 \times (-2))^{-1} \)
  4. Simplifica: \( (\frac{y^4}{y^6})^3 \)
  5. Simplifica: \( (3x^2)^3 \cdot x^{-4} \)
  6. Simplifica: \( \frac{(-a)^7}{(-a)^3 \cdot a^2} \)
  7. Simplifica: \( ((b^{-2})^{-3})^{-1} \)
  8. Simplifica: \( (\frac{x^2 y^{-1}}{xy^2})^{-2} \)
  9. Simplifica: \( \frac{(2^3 \cdot 3^2)^2}{2^4 \cdot 3^5} \)
  10. Simplifica: \( ((-5)^0 \cdot 4^2)^{-1} \)
  11. Simplifica: \( (\frac{a^{-3}}{a^{-5}})^3 \)
  12. Simplifica: \( \frac{(-x^2y)^3}{-(xy^2)^2} \)

11. Multiplicación de Monomios

Multiplicación de Monomios

📐 Procedimiento para Multiplicar Monomios

Para multiplicar monomios, sigue estos tres sencillos pasos:

  1. Multiplica los coeficientes: Son los números que acompañan a las letras, incluyendo sus signos.
  2. Multiplica las partes literales: Son las letras. Si las bases (letras) son iguales, mantén la base y suma sus exponentes.
  3. Junta los resultados: Une el nuevo coeficiente con la nueva parte literal.
💡 Herramientas Clave que Necesitarás

Antes de practicar, recuerda estas dos reglas fundamentales:

  • Ley de los Signos (Multiplicación): Mismos signos dan (+), signos distintos dan (-).
  • Propiedad de Potencias: Para multiplicar potencias de igual base, se conserva la base y se suman los exponentes (\( a^m \times a^n = a^{m+n} \)).
⚠️ ¡Cuidado! Los exponentes se suman, no se multiplican

Un error muy común al aplicar la propiedad de las potencias es multiplicar los exponentes en vez de sumarlos. ¡No caigas en la trampa!

Recuerda siempre la base de la propiedad:
\(x^2 \cdot x^3\) significa \( (x \cdot x) \cdot (x \cdot x \cdot x) \), lo que da un total de 5 equis, es decir, \(x^5\).

El resultado NO es \(x^6\). Esa regla (multiplicar exponentes) se usa para la "potencia de una potencia", como en \( (x^2)^3 \).

Ejemplo: Coeficiente por Monomio

Problema: \( (-6) \times (3x^2) \)

En este caso, nos enfocamos solo en multiplicar el número suelto (coeficiente) por el coeficiente del monomio. La parte literal (las letras) se mantiene igual.

  1. Identifica los coeficientes: -6 y 3.
  2. Multiplícalos (con regla de signos): \( (-6) \times 3 = -18 \).
  3. Conserva la parte literal: \( x^2 \).

Resultado: \( -18x^2 \)

Ejercicios Iniciales: Coeficiente por Monomio

  1. \( 3 \times (4x) \)
  2. \( -5 \times (2y) \)
  3. \( 6 \times (-3b) \)
  4. \( -2 \times (-7a) \)
  5. \( 8 \times (5m) \)
  6. \( -9 \times (3n) \)
  7. \( 11 \times (-2p) \)
  8. \( -10 \times (-4q) \)
Ejemplo: Variable por Variable

Problema: \( (y^3) \cdot (-y^2) \)

Aquí, nos enfocamos en la parte literal. Como las bases ('y') son iguales, aplicamos la propiedad de las potencias.

  1. Aplica la regla de signos: Tenemos un positivo (implícito) por un negativo, el resultado será negativo.
  2. Suma los exponentes: \( y^{3+2} = y^5 \).

Resultado: \( -y^5 \)

Ejercicios Iniciales: Variable por Variable

  1. \( a \cdot a \)
  2. \( b \cdot b^2 \)
  3. \( m^3 \cdot m \)
  4. \( c \cdot (-c) \)
  5. \( p \cdot p^3 \)
  6. \( q^5 \cdot q^2 \)
  7. \( x \cdot (-x^4) \)
  8. \( (-y^3) \cdot (-y^3) \)
Ejemplo: Monomios Simples

Problema: \( (-4a^2) \times (-2a^3) \)

Ahora combinamos los dos pasos anteriores: multiplicamos coeficientes con coeficientes y literales con literales.

  1. Multiplica los coeficientes: \( (-4) \times (-2) = 8 \).
  2. Multiplica la parte literal: \( a^2 \cdot a^3 = a^{2+3} = a^5 \).

Resultado: \( 8a^5 \)

Ejercicios Iniciales: Monomios Simples

  1. \( (2x) \times (5x) \)
  2. \( (-4y) \times y \)
  3. \( (3a) \times (-6a^2) \)
  4. \( (-5b^2) \times (-2b^2) \)
  5. \( (6p) \times (3p^2) \)
  6. \( (-7q^3) \times (4q) \)
  7. \( (10r^2) \times (-3r^2) \)
  8. \( (-2s) \times (-8s) \)

Paso Final: Juntando Todo (Ejemplos Guiados)

Ejemplo 1: \( (-4a^2b) \times (3ab^3) \)

1. Coeficientes: \( -4 \times 3 = -12 \)

2. Parte Literal:

  • Para la 'a': \( a^2 \times a^1 = a^{2+1} = a^3 \)
  • Para la 'b': \( b^1 \times b^3 = b^{1+3} = b^4 \)

3. Resultado Final: \( -12a^3b^4 \)

Ejemplo 2: \( (\frac{2}{5}xy^2z) \times (-10xz^2) \)

1. Coeficientes: \( \frac{2}{5} \times -10 = \frac{-20}{5} = -4 \)

2. Parte Literal:

  • Para la 'x': \( x^1 \times x^1 = x^{1+1} = x^2 \)
  • Para la 'y': \( y^2 \) (se mantiene igual, ya que no hay otra 'y')
  • Para la 'z': \( z^1 \times z^2 = z^{1+2} = z^3 \)

3. Resultado Final: \( -4x^2y^2z^3 \)

Práctica Final: Monomios Completos

Resuelve las siguientes multiplicaciones de monomios:

  1. \( (-2x) \times (4xy) \)
  2. \( (6a^2b) \times (-3ab^2) \)
  3. \( (-5mn) \times (-8m^2n^3) \)
  4. \( (\frac{1}{2}xy^2) \times (-4x^3y) \)
  5. \( (-7) \times (3a^2bc) \)
  6. \( (9p^2q) \times (-2pq) \)
  7. \( (-4xyz) \times (-6x^2yz^3) \)
  8. \( (\frac{3}{4}ab^2) \times (8a^2b) \)
  9. \( (-10m) \times (5m^3n) \)
  10. \( (-12x^2y) \times (-\frac{1}{3}xy^2) \)
  11. \( (5c^3d^2) \times (5cd^3) \)
  12. \( (-z^5) \times (12z) \)
  13. \( (7x^2y^3) \times (-xy) \)
  14. \( (-\frac{2}{3}m^2n) \times (-9mn^3) \)
  15. \( (20a^4b^2c) \times (\frac{1}{4}a^2b^2c^2) \)
  16. \( (-8p^3q^2) \times (-2p^2q^3) \)
  17. \( (x^3y^2z) \times (-xyz) \)
  18. \( (-1.5a^2b) \times (4ab^3) \)
  19. \( (11m^2n^2) \times (-3mn) \)
  20. \( (6x^4) \times (-3y^4) \)

12. Simplificación de Términos Semejantes (Adición y Sustracción)

Simplificación de Términos Semejantes (Adición y Sustracción)

🤓 ¿Qué son los Términos Semejantes?

Piensa en esto como si juntaras frutas. Si tienes 3 manzanas y te dan 5 manzanas más, ahora tienes 8 manzanas. Pero si tienes 3 manzanas y 2 peras, no puedes decir que tienes "5 manziperas", ¿verdad? Sigues teniendo 3 manzanas y 2 peras por separado.

En álgebra, los "términos semejantes" son como el mismo tipo de fruta. Son aquellos que tienen exactamente la misma parte literal (las mismas letras elevadas a los mismos exponentes).

  • \( 7x \) y \( -2x \) son semejantes.
  • \( 4a^2b \) y \( a^2b \) son semejantes.
  • \( 5x \) y \( 5y \) no son semejantes (distinta letra).
  • \( 8m^2 \) y \( 3m^3 \) no son semejantes (mismo letra, pero distinto exponente).
📐 Procedimiento para Simplificar Expresiones
  1. Identifica y agrupa los términos que sean semejantes entre sí.
  2. Suma o resta los coeficientes de cada grupo, aplicando las reglas de los signos que ya conoces.
  3. La parte literal se mantiene exactamente igual.

Práctica Inicial: Habilidades Fundamentales

1. Identificando Términos Semejantes

En la siguiente lista, agrupa los términos que son semejantes entre sí:

\( 5x, \quad -3y^2, \quad 4xy, \quad -x, \quad 6xy, \quad 2x^2, \quad y^2, \quad -8x^2 \)

2. Sumando y Restando Pares Semejantes

  1. \( 7a + 4a \)
  2. \( 10b - 3b \)
  3. \( -8m - 2m \)
  4. \( -5x + 12x \)
  5. \( 9p - 15p \)
  6. \( -4z + (-3z) \)
  7. \( 15c - 25c \)
  8. \( -y + 8y \)
  9. \( 6a^2 + 3a^2 \)
  10. \( 12b^3 - 5b^3 \)
  11. \( -9x^2y - 3x^2y \)
  12. \( -7mn^3 + 15mn^3 \)
  13. \( 20p^4 - 25p^4 \)
  14. \( -ab + (-5ab) \)
  15. \( 18x^2y^2 - 9x^2y^2 \)
  16. \( -3c^5 + 3c^5 \)
  17. \( 15mn + (-8mn) \)
  18. \( -11p^2q - 5p^2q \)
  19. \( x^3y - 10x^3y \)
  20. \( 25a^3b^2 + 15a^3b^2 \)

Ejemplos Guiados: Expresiones Completas

Ejemplo 1: \( 3x - 5y + 2x + 7y \)

1. Identificar y agrupar términos semejantes:

\( (3x + 2x) + (-5y + 7y) \)

2. Operar los coeficientes de cada grupo:

\( (3+2)x + (-5+7)y \)

3. Resultado Final: \( 5x + 2y \)

⚠️ ¡Cuidado con los Paréntesis y el Signo Negativo!

Cuando hay un signo de resta (-) delante de un paréntesis, ese signo le cambia el signo a todos los términos que están adentro. Es un error muy común olvidar esto.

Por ejemplo: \( -(5m + 2n) \) se convierte en \( -5m - 2n \).

Ejemplo 2 (con paréntesis): \( 8m - 3n - (5m + 2n) \)

1. Eliminar el paréntesis (distribuyendo el signo negativo):

\( 8m - 3n - 5m - 2n \)

2. Identificar y agrupar términos semejantes:

\( (8m - 5m) + (-3n - 2n) \)

3. Operar los coeficientes:

\( (8-5)m + (-3-2)n \)

4. Resultado Final: \( 3m - 5n \)

Práctica Final: Expresiones Algebraicas

Simplifica las siguientes expresiones:

  1. \( 5a + 3a - 2a + 7a \)
  2. \( 10x - 4x - 8x + 3x \)
  3. \( -9m + 4p - 6p + 3m \)
  4. \( -p - 7p + 4q - 2q \)
  5. \( 6c - 5c + 8d + 2d - 3c \)
  6. \( 4x - 2y - 3x + 5y \)
  7. \( -7a + 5b - 8a + 4a - 3b \)
  8. \( 9xy - 3x + 4xy - 2x - 5 \)
  9. \( 5a + 3b - (2a - 7b) \)
  10. \( -9x^2 + 4x - 6 + 3x^2 - 2x \)
  11. \( 10mn - 4m^2n + 8mn - 5m^2n \)
  12. \( 6a^2b^2 - 4ab + 8a^2b^2 + 2ab - 3 \)
  13. \( -7a + 5b - 8c + 4a - 3b + 5c \)
  14. \( (5x - 3y) + (2x + 8y) \)
  15. \( 10a - (4b + 6a) - 3b \)

Práctica Final: Expresiones con Paréntesis (Versión Extendida)

Aplica todo lo aprendido para simplificar estas expresiones. Recuerda eliminar los paréntesis primero, prestando especial atención a los signos negativos.

  1. \( (3x + 2y) + (5x - y) \)
  2. \( (7a - 4b) - (3a + 2b) \)
  3. \( (-m + 2n) + (3m - 3n) \)
  4. \( (a^2 + b^2) - (2a^2 - b^2) \)
  5. \( -(p - q) + (p + q) \)
  6. \( -(x^2 + 3y) - (5y - x^2) \)
  7. \( 10m + (5n - 8m) - 2n \)
  8. \( 8p - (4q - 6p) + 3q \)
  9. \( x^2 + (3x - x^2) + 5x \)
  10. \( ab - (2ab + 4a) - 3a \)
  11. \( 15a - 2b - (10a + 3b) \)
  12. \( -y^2 + (x^2 - y^2) - (x^2) \)
  13. \( (a^2 - 3ab) - (b^2 + 2ab) + (a^2 - b^2) \)
  14. \( -(x + y) + (2x - 3y) - (x - 5y) \)
  15. Desafío: \( 5a - [6b - (3a + 2b)] \)
  16. Desafío Mayor: \( x^2 - (y^2 - [2x^2 - (y^2 + x^2)]) \)

13. ley distributiva y factor comun (nueva version)

Ley Distributiva y Factor Común

En esta lección, exploraremos dos conceptos que son como dos caras de la misma moneda: la ley distributiva (que nos permite expandir expresiones) y el factor común (que nos permite contraerlas).

Parte 1: La Ley Distributiva (Expandir)

📐 Procedimiento para Aplicar la Ley Distributiva

La ley distributiva te dice que para multiplicar un término por una suma o resta, debes multiplicar ese término por cada uno de los términos que están dentro del paréntesis.

Fórmulas:

  • \( a(b + c) = ab + ac \)
  • \( a(b - c) = ab - ac \)

Ejemplos Numéricos

Ejemplo 1: \( 3(4 + 5) \)
  1. Afuera por el primero: \( 3 \times 4 = 12 \)
  2. Afuera por el segundo: \( 3 \times 5 = 15 \)
  3. Juntar resultados: \( 12 + 15 = 27 \)

Comprobación: \( 3 \times (4+5) = 3 \times 9 = 27 \)

Ejemplo 2: \( -2(6 - 3) \)
  1. Afuera por el primero: \( (-2) \times 6 = -12 \)
  2. Afuera por el segundo: \( (-2) \times (-3) = +6 \)
  3. Juntar resultados: \( -12 + 6 = -6 \)

Comprobación: \( -2 \times (6-3) = -2 \times 3 = -6 \)

Ejemplos Algebraicos

Ejemplo 3: \( 2(x + y) \)
  1. Afuera por el primero: \( 2 \times x = 2x \)
  2. Afuera por el segundo: \( 2 \times y = 2y \)
  3. Juntar resultados: \( 2x + 2y \)
Ejemplo 4: \( -5(a - 3b) \)
  1. Afuera por el primero: \( (-5) \times a = -5a \)
  2. Afuera por el segundo: \( (-5) \times (-3b) = +15b \)
  3. Juntar resultados: \( -5a + 15b \)
Ejemplo 5: \( x(y - z) \)
  1. Afuera por el primero: \( x \times y = xy \)
  2. Afuera por el segundo: \( x \times (-z) = -xz \)
  3. Juntar resultados: \( xy - xz \)

Práctica (Parte 1): Aplicando la Ley Distributiva

  1. \( 5(6 + 2) \)
  2. \( -3(8 - 4) \)
  3. \( 7(2 - 5) \)
  4. \( -4(-3 - 6) \)
  5. \( 6(x + 3) \)
  6. \( 4(y - 5) \)
  7. \( -2(a + 8) \)
  8. \( -5(b - 2) \)
  9. \( 8(-m - 3) \)
  10. \( -1(p - 7) \)
  11. \( a(x + y) \)
  12. \( x(y - z) \)
  13. \( -b(c + d) \)
  14. \( m(-n + p) \)
  15. \( 2x(3a - 4b) \)
  16. \( -3c(2m + 5n) \)
  17. \( x(x + 5) \)
  18. \( a(3 - a) \)
  19. \( -y(y + 2) \)
  20. \( 3m(m^2 + 2m) \)
  21. \( -2p^2(p - 4) \)
  22. \( 4(a + b - c) \)
  23. \( -2(x - y + z) \)
  24. \( a(x + y - z) \)
  25. \( 3x(x^2 + 2x - 1) \)
  26. \( -5y^2(y - 3y^2 + 1) \)
  27. \( 2x(3a - 2b + c) \)
  28. \( -mn(m^2 - n^2 - mn) \)
  29. \( x^2(3x + 2x^2 + 4) \)
  30. \( (a+b-c)(-3) \)
💡 Conectando las Ideas: La Factorización como Proceso Inverso

Ya viste cómo "repartir" un término para expandir una expresión. Ahora, aprenderás a hacer exactamente lo contrario: mirar una expresión expandida y encontrar qué término se "repartió" originalmente. Este proceso se llama factorizar.

Distribuir: \( \rightarrow 4(x + y) = 4x + 4y \rightarrow \)
Factorizar: \( \leftarrow 4(x + y) = 4x + 4y \leftarrow \)

Parte 2: Factor Común (Factorizar)

🤓 ¿Qué es Factorizar?

Factorizar es el proceso de reescribir una suma o resta como una multiplicación. Para ello, buscamos el Factor Común, que es el "ingrediente" que se repite en todos los términos de la expresión.

📐 Procedimiento para Encontrar el Factor Común
  1. Para los Coeficientes: Encuentra el Máximo Común Divisor (MCD) de los números.
  2. Para la Parte Literal: Busca las letras que se repiten en todos los términos y escoge la que tenga el menor exponente.
  3. Arma el Factor Común: Junta el MCD de los números y las letras comunes.
  4. Divide y Escribe el Paréntesis: Escribe el factor común y abre un paréntesis. Dentro, coloca el resultado de dividir cada término original por el factor común.

Ejemplos Guiados de Factorización

Ejemplo 1: Factorizar \( 5x - 10y \)

Análisis: El Máximo Común Divisor (MCD) entre 5 y 10 es 5. No hay letras que se repitan en ambos términos.

Factor Común: 5

Resultado: \( 5(x - 2y) \)

Ejemplo 2: Factorizar \( -3a - 6b \)

Análisis: El MCD entre 3 y 6 es 3. Como el primer término es negativo, a menudo es útil factorizar también el signo negativo.

Factor Común: -3

Resultado: \( -3(a + 2b) \)

(Nota: Al dividir -6b entre -3, el resultado es +2b)

Ejemplo 3: Factorizar \( x^2 + xy \)

Análisis: No hay un MCD numérico (es 1). La letra que se repite en ambos términos es la x. La de menor exponente es x¹.

Factor Común: x

Resultado: \( x(x + y) \)

Ejemplo 4: Factorizar \( 2a^2 + 4a \)

1. Coeficientes (2 y 4): El MCD es 2.

2. Parte Literal (a² y a): La letra 'a' se repite. La de menor exponente es a¹.

3. Factor Común: Juntamos los resultados: 2a.

4. Dividimos:

  • \( 2a^2 \div 2a = a \)
  • \( 4a \div 2a = 2 \)

Resultado Final: \( 2a(a + 2) \)

Práctica (Parte 2): Encontrando el Factor Común

  1. \( 8x + 12y \)
  2. \( 9a - 6 \)
  3. \( -5m - 10n \)
  4. \( 14p + 21q \)
  5. \( xy + xz \)
  6. \( ab - ac \)
  7. \( m^2 + mn \)
  8. \( p^3 - p^2 \)
  9. \( 6x^2 + 3x \)
  10. \( 10y^3 - 15y^2 \)
  11. \( -8a^2b + 4ab^2 \)
  12. \( 9m^2n - 12mn^2 \)
  13. \( 16p^3q^2 + 24p^2q^3 \)
  14. \( -25x^4y + 15x^2y^3 \)
  15. \( 10a - 15b + 20c \)
  16. \( 9x^2 - 6x + 3 \)
  17. \( -8m^3 - 12m^2 - 4m \)
  18. \( 14a^2b - 21ab^2 + 7ab \)
  19. \( 18x^3y^2 - 27x^2y^3 + 9x^2y^2 \)
  20. \( -10m^4n^2 - 20m^3n^3 - 5m^2n^4 \)
💡 Estrategia: Expandir y Simplificar en Dos Pasos

Cuando te enfrentas a una expresión con varios paréntesis, el camino más seguro es seguir un proceso ordenado de dos pasos:

  1. Paso 1: Expandir (Eliminar Paréntesis)
    Usa la ley distributiva para multiplicar y eliminar todos los paréntesis de la expresión. ¡Presta mucha atención a los signos negativos delante de un paréntesis!
  2. Paso 2: Simplificar (Juntar Términos Semejantes)
    Una vez que tienes una expresión larga y sin paréntesis, agrupa y combina todos los términos semejantes para llegar a la forma más simple.

Desafío: Expandir y Simplificar

Aplica la estrategia de dos pasos para resolver las siguientes expresiones. ¡Presta mucha atención al orden y a los signos al eliminar los paréntesis y corchetes!

  1. \( 4(x - 3y) + 2(x + 5y) \)
  2. \( 3a(2b + c) - 2(3ab + 4ac) \)
  3. \( -5(2m - n) + 4(-m + 3n) \)
  4. \( 2(3p - q) - (5p + 2q) + 4(p - 3q) \)
  5. \( x(y + 2) - y(x - 3) \)
  6. \( a(a+b) - b(a+b) \)
  7. \( 5(x^2 - 2x) + 3x(x - 1) \)
  8. \( -3(a + 2b) + 4b(a - 1) - 2(b - a) \)
  9. Desafío Anidado 1: \( 2[x - 3(y - x)] \)
  10. Desafío Anidado 2: \( 3a - \{2b + [5a - (4b - a)]\} \)
  11. Desafío Anidado 3: \( 2x^2 - [x^2 - \{y - (3x^2 - y)\}] \)
  12. Desafío Anidado 4: \( m - (2m + [ - (m - n) + (2n - m)]) \)
💡 Estrategia Avanzada: Factorizar para Simplificar

A veces, te encontrarás con expresiones que parecen largas y complicadas. Un truco de experto es, en lugar de expandir todo inmediatamente, observar si puedes factorizar primero para agrupar términos. Esto puede simplificar el problema de forma sorprendente.

Observa el ejemplo que discutimos: \( 3x + 3y - x - y \). En vez de operar término a término, podemos agrupar:

\( (3x + 3y) - (x + y) \)

Luego, factorizamos cada grupo:

\( 3(x+y) - 1(x+y) \)

Ahora, \((x+y)\) es un término común. Si tienes 3 de "algo" y le quitas 1 de "algo", te quedan 2 de "algo":

\( 2(x+y) \)

Finalmente, si es necesario, expandimos:

\( 2x + 2y \)

Desafío Final: Factorizar para Simplificar

Usa la estrategia de factorizar primero para simplificar las siguientes expresiones.

  1. \( 3(a+b) + 5(a+b) \)
  2. \( 7(x-y) - 4(x-y) \)
  3. \( 6(m+n) - (m+n) \)
  4. \( 2(p-q) - 8(p-q) \)
  5. \( 2x + 2y + 5x + 5y \)
  6. \( 8a - 8b - 3a + 3b \)
  7. \( 5m + 10n - (m + 2n) \)
  8. \( 3x(a+1) - 5(a+1) \)

14. Jerarquía de Operaciones y Paréntesis

Jerarquía de Operaciones y Paréntesis

Cuando tenemos una expresión matemática con varias operaciones (suma, resta, multiplicación, división, potencias), es fundamental seguir un orden específico para resolverla correctamente. Este orden se conoce como la jerarquía de operaciones.

📐 El Orden de las Operaciones

Para resolver cualquier operación combinada, debes seguir estos pasos en orden estricto:

  1. Paréntesis (P): Primero, resuelve todas las operaciones que estén dentro de paréntesis (), corchetes [] o llaves {}, desde el más interno hacia el más externo.
  2. Potencias (P): Luego, calcula todas las potencias y raíces.
  3. Multiplicación y División (M, D): Después, realiza todas las multiplicaciones y divisiones, operando en el orden en que aparecen, de izquierda a derecha.
  4. Adición y Sustracción (A, S): Finalmente, realiza todas las sumas y restas, operando de izquierda a derecha.
💡 Recordatorio: PAPOMUDAS

Una forma fácil de recordar este orden en Chile es con la palabra PAPOMUDAS:

PAréntesis - POtencias - MUltiplicación - División - Adición - Sustracción

Ejemplos Guiados

Ejemplo 1: Sin Paréntesis

Expresión: \( 5 + 3 \times 2^2 - 6 \div 3 \)

Desarrollo del Cálculo:

 5 + 3 × 2² - 6 ÷ 3 =
 5 + 3 ×  4  - 6 ÷ 3 =
 5 +   12   -    2   =
    17     -    2   =
          15

Explicación Paso a Paso:

  1. Potencias: Primero, calculamos \(2^2 = 4\).
  2. Multiplicación y División (de izquierda a derecha): Calculamos \(3 \times 4 = 12\) y \(6 \div 3 = 2\).
  3. Suma y Resta (de izquierda a derecha): Calculamos \(5 + 12 = 17\) y luego \(17 - 2 = 15\).

Resultado Final: 15

Ejemplo 2: Con Paréntesis

Expresión: \( (5 + 3) \times (2^2 - 6) \div 2 \)

Desarrollo del Cálculo:

 (5 + 3) × (2² - 6) ÷ 2 =
    8    × (4 - 6)  ÷ 2 =
    8    ×   (-2)   ÷ 2 =
       -16       ÷ 2 =
              -8

Explicación Paso a Paso:

  1. Paréntesis: Resolvemos las operaciones dentro de cada uno.
    En el primero: \( 5 + 3 = 8 \).
    En el segundo: \( 2^2 - 6 = 4 - 6 = -2 \).
  2. Multiplicación y División (de izquierda a derecha): Calculamos \(8 \times (-2) = -16\) y luego \(-16 \div 2 = -8\).

Resultado Final: -8

Ejemplo 3: Con Paréntesis Anidados

Expresión: \( 10 - [3 + (4 - 2) \times 5] \)

Desarrollo del Cálculo:

 10 - [3 + (4 - 2) × 5] =
 10 - [3 +    2    × 5] =
 10 - [3 +     10    ] =
 10 - [      13     ] =
 10 - 13 =
 -3

Explicación Paso a Paso:

  1. Paréntesis más interno: Resolvemos \( (4 - 2) = 2 \).
  2. Siguiente paréntesis (corchete): Dentro del corchete, respetamos la jerarquía (primero multiplicación). Calculamos \(2 \times 5 = 10\) y luego \(3 + 10 = 13\).
  3. Resta Final: \( 10 - 13 = -3 \).

Resultado Final: -3

Ejercicios de Práctica Numérica

  1. \( 7 + 3 \times 4 - 5 \)
  2. \( 10 - 2 \times 3 + 4 \)
  3. \( (-2)^3 + 4 \times 5 - 2 \)
  4. \( 6 \div 2 + 3 \times 4 - 1 \)
  5. \( 15 - 3 \times 2^2 + 1 \)
  6. \( (7 + 3) \times 2 - 5 \)
  7. \( 10 - (2 \times 3) + 4 \)
  8. \( (-2)^3 + (4 \times 5 - 2) \)
  9. \( (6 \div 2 + 3) \times 4 - 1 \)
  10. \( 15 - (3 \times 2^2) + 1 \)
  11. \( 5 \times [3 + (2 - 1) \times 4] \)
  12. \( 12 \div [6 - (2 + 1) \times 2] \)
  13. \( (-3)^2 + [4 - (5 - 2) \times 3] \)
  14. \( [8 - (6 \div 3 + 1)] \times 2 \)
  15. \( 20 - [(3 + 2) \times 4 - 10] \)

Desafío Algebraico: Jerarquía de Operaciones con Variables

Ahora que dominas la jerarquía de operaciones con números, aplicaremos las mismas reglas para simplificar expresiones algebraicas. El objetivo es el mismo: seguir el orden correcto para llegar a la expresión más simple posible.

Ejemplo 1: \( 5x + 2(x^2 - 4x) - 3x^2 \)

En esta expresión, la jerarquía nos dice que primero debemos resolver la multiplicación (la distribución del 2).

  1. Paso 1 (Expandir): Aplicamos la ley distributiva.
    \( 5x + 2x^2 - 8x - 3x^2 \)
  2. Paso 2 (Agrupar): Identificamos y agrupamos los términos semejantes.
    \( (2x^2 - 3x^2) + (5x - 8x) \)
  3. Paso 3 (Simplificar): Resolvemos las sumas y restas.
    \( -x^2 - 3x \)

Resultado Final: \( -x^2 - 3x \)

Ejemplo 2 (con corchetes): \( 3[a - (2a + 1)] + 7 \)

Aquí, resolvemos desde el paréntesis más interno hacia afuera.

  1. Paso 1 (Paréntesis interno): Eliminamos el paréntesis redondo, distribuyendo el signo negativo.
    \( 3[a - 2a - 1] + 7 \)
  2. Paso 2 (Simplificar dentro del corchete): Juntamos los términos semejantes dentro del corchete.
    \( 3[-a - 1] + 7 \)
  3. Paso 3 (Expandir): Aplicamos la ley distributiva con el 3.
    \( -3a - 3 + 7 \)
  4. Paso 4 (Simplificar final): Sumamos los números.
    \( -3a + 4 \)

Resultado Final: \( -3a + 4 \)

🏆 Desafío Final: Combinando Propiedades y Operaciones

¡Es hora de unirlo todo! En los siguientes ejercicios, necesitarás usar la jerarquía de operaciones (PAPOMUDAS) junto con las propiedades de las potencias y la simplificación de términos semejantes para encontrar la respuesta final.

  1. \( 5(x + 3) + 2x \)
  2. \( 4a + 3(a - 2) \)
  3. \( 8y - 2(3y + 4) \)
  4. \( x(x + 6) - x^2 \)
  5. \( 3m(m - 2) + 6m \)
  6. \( -4b(2 - b) + 5b^2 \)
  7. \( (2x^2 \cdot 3x) + 4(x^3 - 2x) \)
  8. \( 10p^2 - (p \cdot 5p) + 3p \)
  9. \( 2[3(x+5) - x] \)
  10. \( a[4a - (a + 2)] + 5a \)
  11. \( -3[b^2 - 2(b^2 + b)] \)
  12. \( x^2 + 2[x(x-3) - (x^2 - 6x)] \)

Problemas de Aplicación

  1. Un camión transporta 25 cajas de manzanas (30 kg c/u) y 10 sacos de papas (50 kg c/u). Si descarga 5 cajas de manzanas y 3 sacos de papas, ¿cuántos kg de carga le quedan?
  2. En un torneo, un jugador con 200 puntos gana 3 partidas (+150 puntos c/u) y luego pierde 2 partidas (-80 puntos c/u). ¿Cuál es su puntaje final?
  3. Una tienda tiene una oferta: "Compre 2 camisas a $25 c/u y la tercera a mitad de precio". Si un cliente compra 5 camisas, ¿cuánto paga?
  4. Un restaurante ofrece un menú con 4 entradas, 5 platos principales y 3 postres. ¿Cuántas combinaciones diferentes de menú se pueden formar?
  5. Un automovilista conduce 3 horas a 80 km/h, se detiene 30 minutos, y luego conduce 2 horas más a 70 km/h. ¿Cuántos kilómetros recorrió en total?

15. Operaciones con Valor Absoluto

Operaciones con Valor Absoluto

🤓 ¿Qué significa operar con valor absoluto?

Cuando aparece una expresión como \( |a - b| \), primero se calcula lo que está dentro de las barras (el argumento), y luego se aplica el valor absoluto.

El valor absoluto representa la distancia al cero, por lo tanto el resultado siempre es positivo o cero.

📐 Pasos para resolver:

  1. Resuelve lo que está dentro de las barras.
  2. Aplica el valor absoluto (elimina el signo negativo si lo hay).

Ejemplo: \( |3 - 7| = |-4| = 4 \)

🧪 Práctica Guiada:

  1. \( |5 - 8| \)
  2. \( |-3 + 4| \)
  3. \( |(-2)^2 - 5| \)
  4. \( ||4| - |7|| \)
  5. \( |(-6) \cdot 3| \)
  6. \( |-(-8)| \)
  7. \( |10 - (-5)| \)
  8. \( ||-9| - 3| \)
  9. \( |(-4)^2 - 20| \)
  10. \( |0 - (-7)| \)
  11. \( |-(3 \cdot 4)| \)
  12. \( ||2| + |-5|| \)

💡 Consejo:

Resuelve siempre primero lo que está dentro de las barras. Si la expresión tiene varias operaciones, recuerda usar la jerarquía de operaciones (paréntesis → potencias → multiplicación/división → suma/resta).

🎯 Desafíos con Literales:

  1. Si \( x = -3 \), calcula \( |x + 5| \)
  2. Si \( a = -4 \) y \( b = 2 \), calcula \( ||a| - |b|| \)
  3. Si \( m = -6 \), calcula \( |m| + |-m| \)
  4. Si \( y = -2 \), calcula \( |(y)^2 - 5| \)