Los datos estan dispersos?
8. Interpretación y Comparación con Medidas de Dispersión
Interpretación y Comparación con Medidas de Dispersión
Repaso: Medidas de Dispersión
Recordemos que las medidas de dispersión (rango, varianza, desviación estándar) nos indican qué tan "esparcidos" o "concentrados" están los datos alrededor de la media. Son fundamentales para comprender la variabilidad de un conjunto de datos.
Interpretación Conjunta de Media y Desviación Estándar
La media y la desviación estándar se interpretan *juntas* para tener una idea completa de la distribución de los datos. La media nos da el "centro" y la desviación estándar nos dice qué tan "anchos" son los datos alrededor de ese centro.
Ejemplo:
- Conjunto A: Media = 50, Desviación estándar = 5
- Conjunto B: Media = 50, Desviación estándar = 15
Ambos conjuntos tienen la misma media (50), pero el Conjunto B tiene una desviación estándar mucho mayor. Esto significa que:
- En el Conjunto A, la mayoría de los datos estarán relativamente cerca de 50 (probablemente entre 45 y 55, o entre 40 y 60, si consideramos dos desviaciones estándar).
- En el Conjunto B, los datos estarán mucho más dispersos. Es más probable encontrar valores significativamente más alejados de 50 (por ejemplo, valores por debajo de 35 o por encima de 65).
Comparación de Conjuntos de Datos
Podemos usar la media y la desviación estándar para comparar diferentes conjuntos de datos, incluso si tienen unidades diferentes (aunque en ese caso, es mejor usar el coeficiente de variación, que veremos más adelante).
Ejemplo (mismas unidades): Dos clases rinden el mismo examen:
- Clase X: Media = 75, Desviación estándar = 8
- Clase Y: Media = 75, Desviación estándar = 3
Conclusión: Ambas clases tienen el mismo promedio, pero la Clase Y tiene notas mucho más homogéneas (menos dispersas) que la Clase X.
Ejemplo (contexto diferente): Edades de dos grupos:
- Grupo P: Media = 25 años, Desviación estándar = 2 años
- Grupo Q: Media = 60 años, Desviación estándar = 10 años
Conclusión: Grupo P son más jovenes que el grupo Q, y además las edades del grupo P son mas homogeneas que el grupo Q
Diagramas de Caja y Bigotes (Boxplots)
Los diagramas de caja y bigotes (boxplots) son una forma visual de representar la dispersión de un conjunto de datos. No vamos a entrar en detalle sobre cómo construirlos, pero es importante saber *interpretarlos*.
Un boxplot muestra:
- Mediana: Una línea dentro de la caja.
- Cuartiles (Q1 y Q3): Los bordes de la caja. El 50% de los datos está *dentro* de la caja (entre Q1 y Q3). Este rango se llama *rango intercuartílico* (IQR).
- "Bigotes": Líneas que se extienden desde la caja hasta los valores máximo y mínimo *dentro de un cierto rango* (generalmente, 1.5 veces el IQR).
- Valores Atípicos (Outliers): Puntos individuales que se muestran *fuera* de los bigotes. Son valores inusualmente altos o bajos.
Ejemplo:
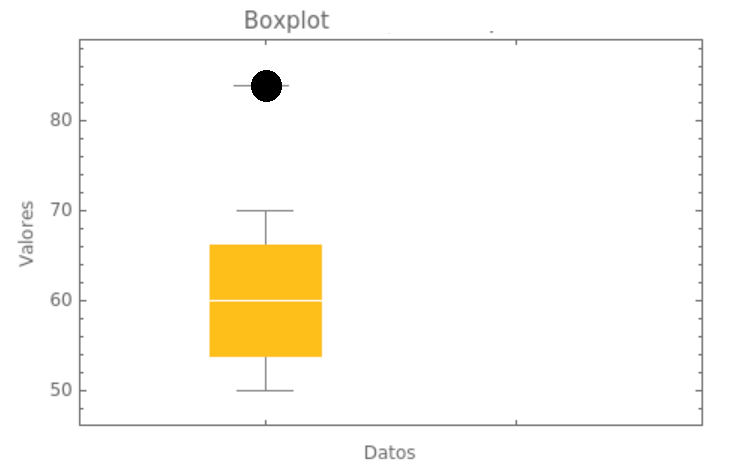
Lectura de la imagen
- La mediana está en 60.
- El primer cuartil (Q1) está en 55.
- El tercer cuartil (Q3) está en 65.
- Los "bigotes" se extienden hasta 50 y 70.
- Hay un punto atípico en 85.
Interpretación:
- El valor "típico" de los datos es alrededor de 60 (la mediana).
- El 50% central de los datos está entre 55 y 65.
- La mayoría de los datos están entre 50 y 70.
- Hay un valor inusualmente alto (85) que se considera un valor atípico.
Valores Atípicos (Outliers)
Identificación (Regla General)
Una regla general para identificar valores atípicos es la regla del "1.5 veces el IQR":
- Calcula el Rango Intercuartílico (IQR) = Q3 - Q1.
- Calcula los "límites":
- Límite inferior = Q1 - 1.5 * IQR
- Límite superior = Q3 + 1.5 * IQR
- Cualquier valor *fuera* de estos límites se considera un valor atípico.
Ejemplo:
Datos: 2, 3, 5, 7, 8, 9, 10, 12, 15, 25
- Q1 = 4 (mediana de la primera mitad de los datos)
- Q3 = 11 (mediana de la segunda mitad de los datos)
- IQR = 11-4=7
- Límite inferior: 4 - 1.5 * 7 = -6.5
- Límite superior: 11 + 1.5 * 7 = 21.5
El valor 25 es un valor atípico, ya que es mayor que 21.5
Importancia
Los valores atípicos pueden deberse a errores de medición, errores de registro, o pueden ser valores válidos pero inusuales. Es importante identificarlos porque:
- Pueden distorsionar las medidas de tendencia central (especialmente la media) y las medidas de dispersión.
- Pueden indicar información importante sobre el proceso o fenómeno que se está estudiando.
No siempre se deben eliminar los valores atípicos. Hay que investigarlos y decidir si se eliminan, se corrigen o se mantienen, según el contexto.
Ejercicios y Problemas
Ejercicio 1: Dados los siguientes conjuntos de datos, interpreta la media y la desviación estándar en términos de la dispersión de los datos:
- Conjunto X: Media = 10, Desviación estándar = 2
- Conjunto Y: Media = 10, Desviación estándar = 8
- Conjunto Z: Media = 100, Desviación estándar = 10
Ejercicio 2: Dados los siguientes boxplots (Diagramas de caja y bigotes)
Boxplot A:
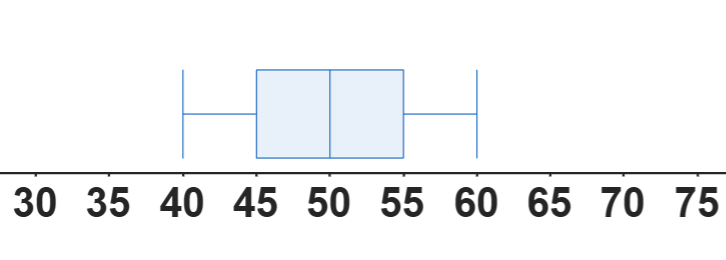
Boxplot B:
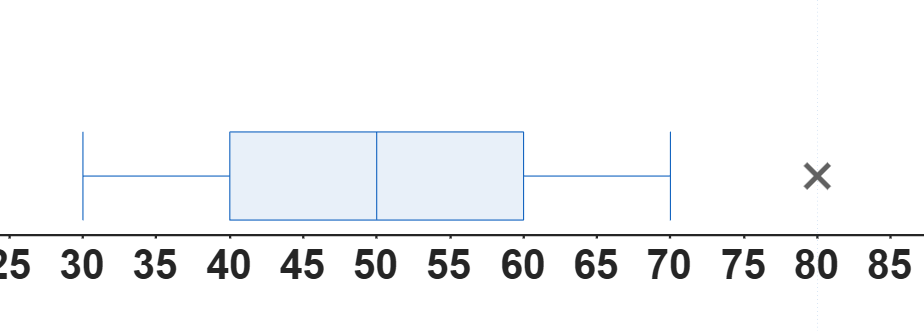
- ¿Qué boxplot representa datos con mayor dispersión?
- ¿Cuál boxplot indica la presencia de un valor atípico?
Ejercicio 3: Para el siguiente conjunto de datos, identifica si hay valores atípicos utilizando la regla del 1.5 * IQR:
1, 3, 5, 7, 8, 9, 10, 12, 14, 30
Problema 1: Dos empresas, A y B, fabrican bombillas. Se prueban muestras de bombillas de cada empresa y se registra su duración (en horas):
Empresa A: Media = 1000 horas, Desviación estándar = 50 horas
Empresa B: Media = 1000 horas, Desviación estándar = 150 horas
- ¿Qué empresa produce bombillas con una duración más consistente (menos variable)?
- Si quieres comprar bombillas que duren *alrededor* de 1000 horas, ¿qué empresa elegirías? ¿Por qué?
- Si necesitas buscar bombillas que duren mas de 1100 horas, ¿qué empresa elegirías? ¿Por qué?
Problema 2: Se registran las alturas (en cm) de los estudiantes de dos clases:
Clase 1: 160, 165, 170, 175, 180
Clase 2: 150, 160, 170, 180, 190
- Calcula la media y la desviación estándar (muestral) para cada clase.
- ¿Qué clase tiene mayor variabilidad en las alturas?
- Si se agrega un estudiante de 200 cm a la Clase 1, ¿cómo afectaría esto a la media y a la desviación estándar? ¿Y si se agrega a la Clase 2?
© 2025 - Material de Apoyo
Problema 1: Tiempos de Atención en un Banco
Este tipo de análisis es crucial para la gestión de servicios. Un banco podría usar estos datos para decidir si necesita contratar más personal en una sucursal, mejorar sus procesos o redistribuir a sus empleados para que los tiempos de espera sean más consistentes y bajos para los clientes.
Se realiza un estudio sobre el tiempo (en minutos) que tardan los clientes en ser atendidos en dos sucursales de un banco. Los datos se consideran una muestra.
Sucursal A:
| Tiempo (min) | Frecuencia |
|---|---|
| [0 - 5) | 10 |
| [5 - 10) | 15 |
| [10 - 15) | 8 |
| [15 - 20) | 5 |
| [20 - 25) | 2 |
Sucursal B:
| Tiempo (min) | Frecuencia |
|---|---|
| [0 - 5) | 5 |
| [5 - 10) | 10 |
| [10 - 15) | 15 |
| [15 - 20) | 12 |
| [20 - 25) | 8 |
- Calcula la media y la desviación estándar para cada sucursal.
- ¿En qué sucursal los tiempos de atención son más consistentes? Justifica con los datos.
- Si fueras un cliente, ¿en qué sucursal es más probable que tengas que esperar más de 15 minutos? Justifica.
a) Cálculos para cada sucursal:
Sucursal A:
- Media (\(\bar{x}_A\)): \(8.75\) minutos
- Desviación Estándar (\(s_A\)): \(5.72\) minutos
Sucursal B:
- Media (\(\bar{x}_B\)): \(12.8\) minutos
- Desviación Estándar (\(s_B\)): \(6.09\) minutos
b) Consistencia de los tiempos: La consistencia se mide con la desviación estándar. Una menor desviación estándar implica mayor consistencia. La Sucursal A tiene una desviación estándar (\(s_A \approx 5.72\)) menor que la Sucursal B (\(s_B \approx 6.09\)), por lo tanto, sus tiempos de atención son más consistentes o predecibles.
c) Probabilidad de esperar más de 15 minutos: Para responder a esto, miramos la frecuencia relativa en los intervalos de 15 minutos o más.
- Sucursal A: \(5+2 = 7\) clientes de un total de 40 esperaron más de 15 min. Esto es \(\frac{7}{40} = 17.5\%\).
- Sucursal B: \(12+8 = 20\) clientes de un total de 50 esperaron más de 15 min. Esto es \(\frac{20}{50} = 40\%\).
Por lo tanto, es mucho más probable esperar más de 15 minutos en la Sucursal B.

