Los datos estan dispersos?
3. Organización de Datos en Tablas e Interpretación Gráfica
Organización de Datos en Tablas e Interpretación Gráfica
🤓 Nota del Profesor: Antes de poder analizar qué tan "dispersos" están nuestros datos, primero debemos ser capaces de ordenarlos y visualizarlos de manera efectiva. Las tablas y los gráficos son nuestras herramientas principales para transformar una lista caótica de números en información útil.
Tipos de Tablas de Frecuencias
Dependiendo de la naturaleza de los datos, usamos distintas tablas para organizarlos.
| Tipo de Tabla | Uso Principal | Ejemplo de Datos |
|---|---|---|
| tabla de registros o datos sueltos | Cuando hay un registro de cada uno de los datos y no han sido agrupados. | Sueldo específico de cada trabajador, registros de RUT. |
| Frecuencias para Datos no Agrupados | Cuando tenemos un número manejable de valores distintos que se repiten. | Notas de un curso (valores del 1 al 7), número de hijos por familia. |
| Frecuencias para Datos Agrupados | Cuando tenemos muchos valores distintos o son datos continuos. | Alturas de personas, peso de objetos, tiempo de espera en una fila. |
Ejemplos de Tablas para Organizar Datos
🧪 Ejemplo: Tabla de Datos Simple
En estos registros de altura no hay valores repetidos.
Datos: Alturas (cm) de 5 estudiantes.
| Estudiante | Altura (cm) |
|---|---|
| 1 | 160 |
| 2 | 165 |
| 3 | 170 |
| 4 | 172 |
| 5 | 168 |
🧪 Ejemplo: Tabla de Frecuencias (Datos no Agrupados)
Aqui hay edades que se repiten, asi que se muestra cada edad una sola vez y su frecuencia respectiva (cuántas veces aparece).
Datos: Edades de 10 estudiantes: 20, 22, 20, 21, 22, 20, 23, 22, 20, 21.
| Edad | Frecuencia (f) | Frecuencia Relativa (%) |
|---|---|---|
| 20 | 4 | 40% |
| 21 | 2 | 20% |
| 22 | 3 | 30% |
| 23 | 1 | 10% |
| Total | 10 | 100% |
🧪 Ejemplo: Tabla de Frecuencias (Datos Agrupados)
Aqui con 40 estudiantes hay muchas estaturas distintas mejor las agrupamos en intervalos o clases.
Datos: Alturas (cm) de 40 estudiantes.
| Intervalo de Altura (cm) | Frecuencia (f) |
|---|---|
| 150 - 159 | 5 |
| 160 - 169 | 12 |
| 170 - 179 | 15 |
| 180 - 189 | 8 |
| Total | 40 |
💡 ¿Cuándo agrupar en intervalos?
Agrupar datos en intervalos o "clases" es útil para simplificar un conjunto de datos grande y continuo. Al hacerlo, recuerda estas reglas generales:
- Todos los intervalos deben tener la misma amplitud.
- Los intervalos no deben superponerse.
- Deben cubrir todo el rango de tus datos, desde el mínimo hasta el máximo.
- Una buena práctica es usar entre 5 y 15 intervalos (regla práctica: raíz cuadrada del número de datos).
Interpretación Visual de la Dispersión
Los gráficos nos permiten "ver" la dispersión de los datos de un solo vistazo.
Histogramas
Un histograma nos muestra la forma de la distribución de los datos. Observando su forma, podemos estimar visualmente la dispersión:
- Un histograma alto y estrecho indica baja dispersión (datos muy concentrados alrededor de la media).
- Un histograma ancho y plano indica alta dispersión (datos muy esparcidos).
Diagramas de Caja (Boxplots)
Estos diagramas son un resumen visual de cinco números clave y son excelentes para comparar la dispersión entre distintos grupos.
📐 Componentes de un Diagrama de Caja:
- Mediana (Q2): La línea que divide la caja en dos.
- Caja: Contiene el 50% central de los datos. Sus bordes son el primer cuartil (Q1) y el tercer cuartil (Q3).
- Rango Intercuartílico (IQR): Es el ancho de la caja (Q3 - Q1). Un IQR más grande implica mayor dispersión en el centro de los datos.
- Bigotes: Las líneas que se extienden desde la caja. Indican la dispersión de los datos fuera del 50% central.
- Valores Atípicos (Outliers): Puntos individuales fuera de los bigotes, que representan valores inusualmente altos o bajos.
🧪 Ejemplo: Comparación de Boxplots
Analicemos la dispersión de tres conjuntos de datos (j, k, l) a través de sus diagramas de caja.
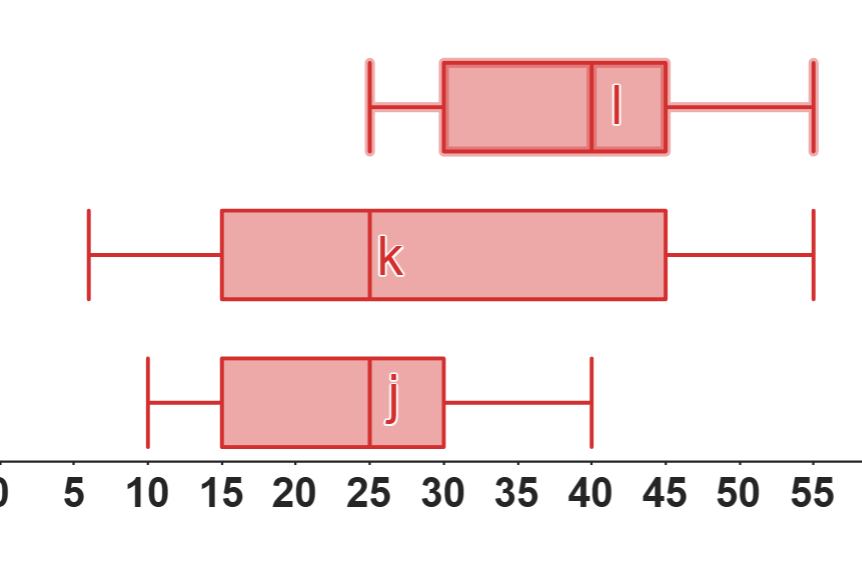
A continuación, se resumen las diferencias clave que podemos observar:
| Característica | j | k | l |
|---|---|---|---|
| Rango (Dispersión Total) | Bajo (10 a 40) | Muy Alto (5 a 55) | Bajo (25 a 55) |
| Rango Intercuartílico (IQR) | Bajo (15) | Alto (30) | Bajo (15) |
| Simetría | Relativamente simétrico | Asimétrico a la derecha | Asimétrico a la izquierda |
| Conclusión | Datos consistentes y bajos. | Datos muy variables y dispersos. | Datos consistentes y altos. |
Ejercicios y Problemas
✍️ Ejercicio 1: Tabla de Frecuencias
Las calificaciones de 20 estudiantes son: 7, 8, 6, 5, 9, 7, 8, 10, 6, 7, 7, 8, 9, 5, 6, 8, 7, 4, 9, 7. Organiza los datos en una tabla de frecuencias y calcula la frecuencia relativa de cada calificación.
| Calificación | Frecuencia Absoluta | Frecuencia Relativa |
|---|---|---|
| 4 | 1 | 0.05 (5%) |
| 5 | 2 | 0.10 (10%) |
| 6 | 3 | 0.15 (15%) |
| 7 | 6 | 0.30 (30%) |
| 8 | 4 | 0.20 (20%) |
| 9 | 3 | 0.15 (15%) |
| 10 | 1 | 0.05 (5%) |
| Total | 20 | 1.00 (100%) |
✍️ Ejercicio 2: Datos Agrupados
Los pesos (kg) de 30 paquetes son: 1.2, 1.5, 1.8, 2.1, 1.3, 1.6, 1.9, 2.0, 1.4, 1.7, 1.2, 1.5, 2.3, 1.8, 1.6, 1.4, 1.7, 2.0, 1.9, 1.3, 1.5, 1.8, 2.2, 1.7, 1.4, 1.6, 2.1, 1.9, 1.5, 1.8. Agrupa los datos en una tabla de frecuencias con intervalos de ancho 0.4 kg, comenzando en 1.2 kg.
| Intervalo de Peso (kg) | Frecuencia |
|---|---|
| 1.2 - 1.5 | 11 |
| 1.6 - 1.9 | 13 |
| 2.0 - 2.3 | 6 |
| Total | 30 |
✍️ Ejercicio 3: Interpretación de Histogramas
Observa los siguientes histogramas (descritos):
- Histograma A: Simétrico y estrecho, centrado en 50.
- Histograma B: Sesgado a la derecha, la mayoría de datos entre 20 y 40.
- Histograma C: Ancho y plano, extendiéndose de 10 a 90.
¿Qué histograma tiene la mayor desviación estándar? ¿Y la menor?
- Mayor desviación estándar: Histograma C (es el más ancho y plano, indica mayor dispersión).
- Menor desviación estándar: Histograma A (es el más estrecho, indica la menor dispersión).
✍️ Problema 1: Comparando la Dispersión
Se te presentan dos diagramas de caja:
- Boxplot X: Mediana = 30, IQR = 10 (Q1=25, Q3=35), sin valores atípicos.
- Boxplot Y: Mediana = 30, IQR = 20 (Q1=20, Q3=40), con un valor atípico en 60.
¿Qué boxplot representa datos con mayor dispersión? Justifica.
El Boxplot Y representa datos con mayor dispersión. Su Rango Intercuartílico (IQR) es de 20, el doble que el de X, lo que significa que el 50% central de sus datos está mucho más esparcido. Además, la presencia de un valor atípico también indica una mayor variabilidad general.
✍️ Problema 2: Análisis de Consultorios
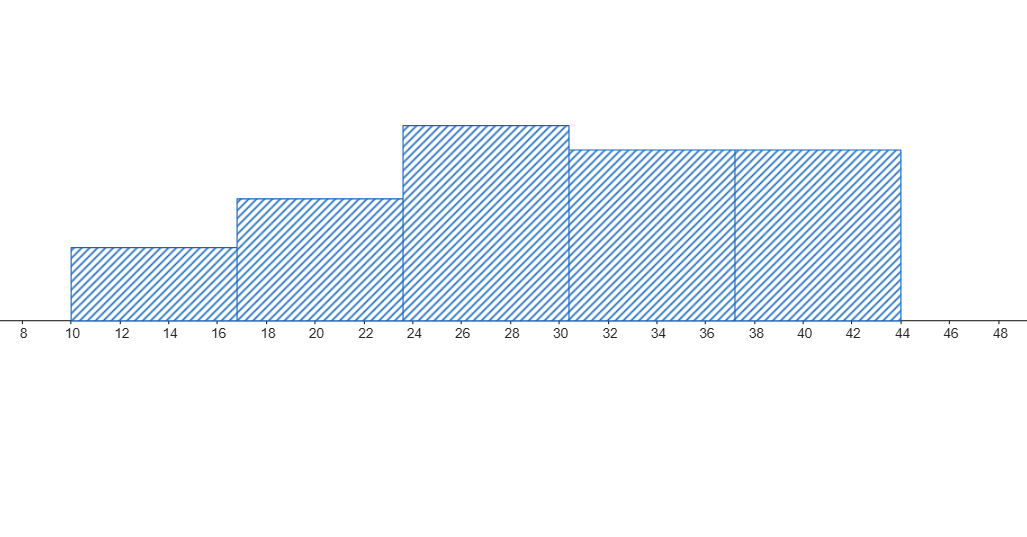
Observa los gráficos (histograma y boxplot) de los tiempos de espera en dos consultorios médicos y responde:
Consultorio A
Consultorio B
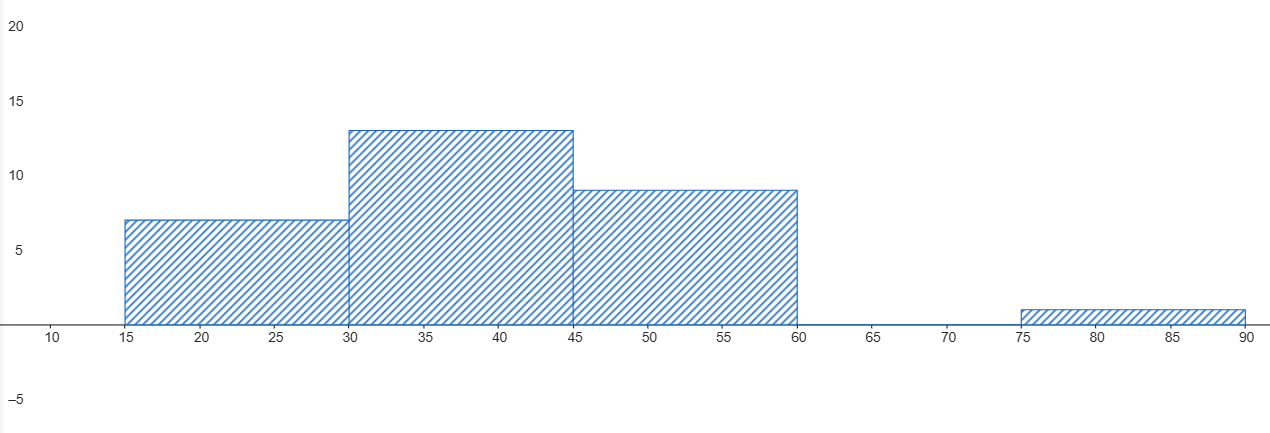
- ¿Qué consultorio tiene, en promedio, tiempos de espera más largos?
- ¿En qué consultorio los tiempos son más variables (mayor dispersión)?
- Si tuvieras prisa, ¿a qué consultorio irías y por qué?
- El Consultorio B tiene tiempos de espera más largos en promedio (su mediana en el boxplot y el centro de su histograma están más a la derecha).
- El Consultorio B tiene tiempos más variables (su histograma es más ancho y su boxplot tiene una caja y bigotes más largos).
- Iría al Consultorio A. Aunque no garantiza el menor tiempo, su menor dispersión y menor promedio lo hacen la apuesta más segura para una espera corta.
© 2025 - Material de Apoyo Actualizado

