Los números naturales
12. Potencias de Números Naturales
Potencias de Números Naturales
Una potencia es una forma abreviada de escribir una multiplicación de un número por sí mismo varias veces. Se compone de una base y un exponente. La base es el número que se multiplica por sí mismo, y el exponente indica cuántas veces se multiplica la base.
Ejemplo:
\(2^3 = 2 \times 2 \times 2 = 8\)
En este ejemplo, 2 es la base y 3 es el exponente. Se lee "2 elevado a la potencia 3" o "2 al cubo".
Elementos de una Potencia
- Base: Es el número que se multiplica por sí mismo.
- Exponente: Indica cuántas veces se multiplica la base por sí misma.
- Potencia: Es el resultado de la operación.
Ejemplos de Potencias
- \(3^2 = 3 \times 3 = 9\) ("3 al cuadrado" o "3 a la potencia 2")
- \(5^4 = 5 \times 5 \times 5 \times 5 = 625\) ("5 a la cuarta" o "5 a la potencia 4")
- \(10^3 = 10 \times 10 \times 10 = 1000\) ("10 al cubo" o "10 a la potencia 3")
- \(1^5 = 1 \times 1 \times 1 \times 1 \times 1 = 1\) ("1 a la quinta" o "1 a la potencia 5")
- \(7^0 = 1\) ("7 a la cero")
Ejercicios de Potencias
- \(2^4\) = 16
- \(4^3\) = 64
- \(6^2\) = 36
- \(3^5\) = 243
- \(9^3\) = 729
- \(10^6\) = 1000000
- \(15^2\) = 225
- \(1^{10}\) = 1
- \(8^0\) = 1
- \(20^2\) = 400
El Árbol de Potencias
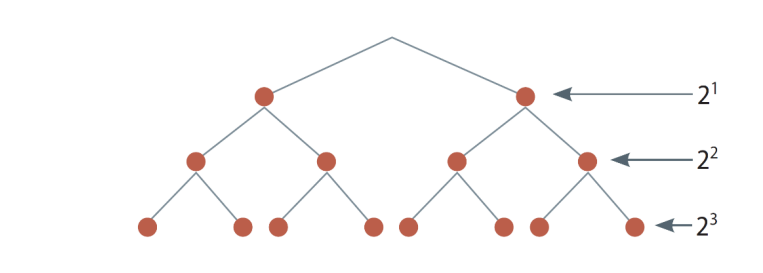
El árbol de potencias es una forma visual de entender cómo se construyen las potencias. Se empieza con la base en la parte inferior (la "raíz") y se va multiplicando por la base a medida que se sube por el árbol. Cada nivel del árbol representa un exponente.
Ejemplo con base 2:
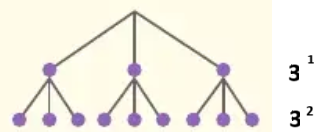
Ejemplo con base 3:
Como se puede ver en el árbol, cada nivel se obtiene multiplicando el nivel anterior por la base. También se puede deducirr que cualquier número elevado a la potencia 0 es 1 (excepto el 0).
Encontrar la Base
En algunos casos, se nos da la potencia y el exponente, y se nos pide encontrar la base. Para esto, necesitamos pensar en qué número multiplicado por sí mismo la cantidad de veces que indica el exponente nos da la potencia.
Ejemplos:
- Si \(x^2 = 9\), entonces \(x = 3\) porque \(3 \times 3 = 9\)
- Si \(x^3 = 8\), entonces \(x = 2\) porque \(2 \times 2 \times 2 = 8\)
- Si \(x^4 = 16\), entonces \(x = 2\) porque \(2 \times 2 \times 2 \times 2 = 16\)
Ejercicios de Encontrar la Base
- Si \(x^2 = 25\), ¿cuánto vale \(x\)? x = 5
- Si \(x^3 = 27\), ¿cuánto vale \(x\)? x = 3
- Si \(x^4 = 81\), ¿cuánto vale \(x\)? x = 3
- Si \(x^2 = 100\), ¿cuánto vale \(x\)? x = 10
- Si \(x^3 = 64\), ¿cuánto vale \(x\)? x = 4
- Si \(x^5 = 32\), ¿cuánto vale \(x\)? x = 2
- Si \(x^2 = 144\), ¿cuánto vale \(x\)? x = 12
- Si \(x^3 = 125\), ¿cuánto vale \(x\)? x = 5
- Si \(x^4 = 625\), ¿cuánto vale \(x\)? x = 5
- Si \(x^6 = 1\), ¿cuánto vale \(x\)? x = 1
Problemas Básicos con Potencias
- Un edificio tiene 4 pisos. Cada piso tiene 4 departamentos, y en cada departamento viven 4 personas. ¿Cuántas personas viven en el edificio? (Expresa la solución usando potencias) \(4^3 = 64\) personas
- Una bacteria se duplica cada hora. Si al principio hay una bacteria, ¿cuántas bacterias habrá después de 5 horas? (Expresa la solución usando potencias) \(2^5 = 32\) bacterias
- Juan ahorra dinero de la siguiente manera: el primer día ahorra 1 peso, el segundo día ahorra 2 pesos, el tercer día ahorra 4 pesos, y así sucesivamente, duplicando la cantidad cada día. ¿Cuánto dinero tendrá ahorrado al cabo de una semana? (Expresa la solución usando potencias) \(2^7 - 1 = 127\) pesos
- En un tablero de ajedrez, hay 1 grano de trigo en el primer casillero, 2 en el segundo, 4 en el tercero, y así sucesivamente, duplicando la cantidad en cada casillero. ¿Cuántos granos de trigo hay en el quinto casillero? (Expresa la solución usando potencias) \(2^4 = 16\) granos
- María tiene una cadena de mensajes que envía a 3 amigos. Cada amigo reenvía el mensaje a otros 3 amigos, y cada uno de estos lo reenvía a otros 3 amigos. ¿Cuántas personas habrán recibido el mensaje después de la tercera ronda de reenvíos? (Expresa la solución usando potencias) \(3^3 = 27\) personas