semejanzas y escalas
2. Semejanza de Figuras Geométricas
Semejanza de Figuras Geométricas
Definición:
Recordemos que dos figuras geométricas son semejantes si tienen la misma forma, pero no necesariamente el mismo tamaño. Una figura puede ser una versión a escala de la otra (más grande o más pequeña). La congruencia es un caso especial de semejanza, donde la razón de semejanza es exactamente 1. Es decir, dos figuras congruentes son semejantes, pero dos figuras semejantes no son necesariamente congruentes.
Características Clave de Figuras Semejantes:
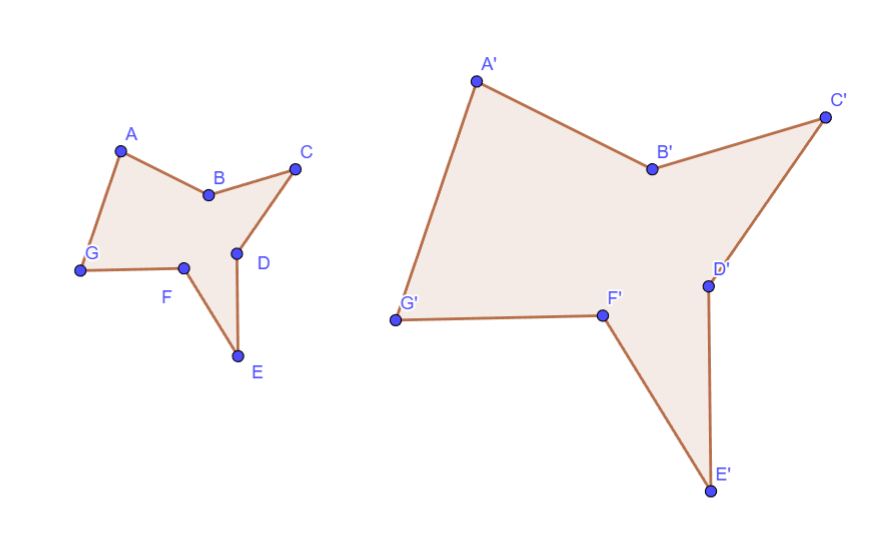
Semejanza de Polígonos:
Para que dos polígonos sean semejantes, deben cumplirse todas las siguientes condiciones:
- Mismo Número de Lados: Deben tener la misma cantidad de lados.
- Ángulos Correspondientes Congruentes: Todos los pares de ángulos correspondientes deben medir lo mismo.
- Lados Correspondientes Proporcionales: La razón entre las longitudes de los lados correspondientes debe ser la misma para todos los pares de lados.
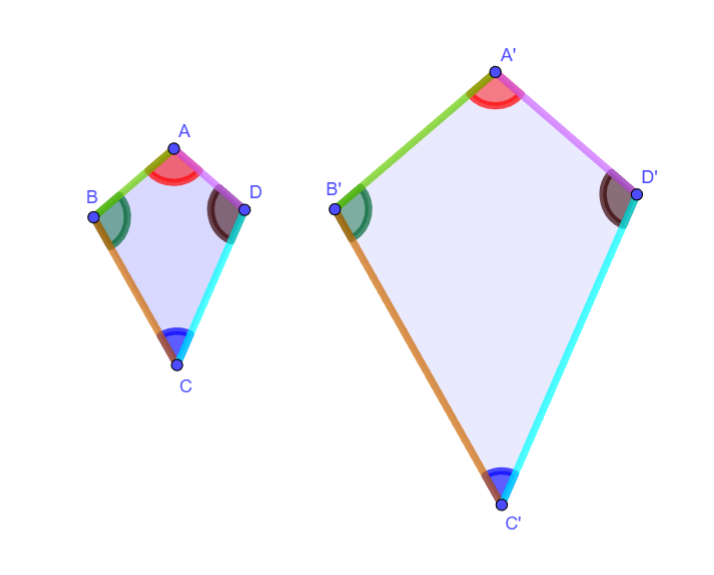
Ejemplo y contraejemplo:
- Todos los cuadrados son semejantes entre sí. Siempre tienen ángulos de 90 grados, y la razón de semejanza es simplemente la proporción entre las longitudes de sus lados.
- Un rectángulo y un cuadrado no son semejantes en general, a menos que el rectángulo también sea un cuadrado. Aunque pueden tener ángulos correspondientes iguales (todos rectos), sus lados no serán proporcionales a menos que sea un caso especial.
Semejanza de Triángulos (Caso Especial Importante):
Los triángulos son un caso especial, y existen criterios específicos que simplifican la determinación de la semejanza. No es necesario verificar todas las condiciones; basta con cumplir uno de estos criterios:
-
Criterio Ángulo-Ángulo (AA): Si dos triángulos tienen dos ángulos correspondientes congruentes, entonces son semejantes. (Si dos ángulos son iguales, el tercero también lo es).
-
Criterio Lado-Lado-Lado (LLL): Si los tres lados de un triángulo son proporcionales a los tres lados correspondientes de otro triángulo, entonces son semejantes.
-
Criterio Lado-Ángulo-Lado (LAL): Si dos triángulos tienen un ángulo correspondiente congruente, y los lados que forman ese ángulo son proporcionales, entonces son semejantes.
Una Definición Alternativa de Semejanza de Polígonos:
Dos polígonos son semejantes si se pueden descomponer en el mismo número de triángulos semejantes, dispuestos de la misma manera. Es decir, si podemos trazar diagonales en ambos polígonos de tal forma que obtengamos triángulos, y cada triángulo en un polígono es semejante a su triángulo correspondiente en el otro polígono.
Por ejemplo si deseamos saber si el siguiente par de poligonos son semejantes....
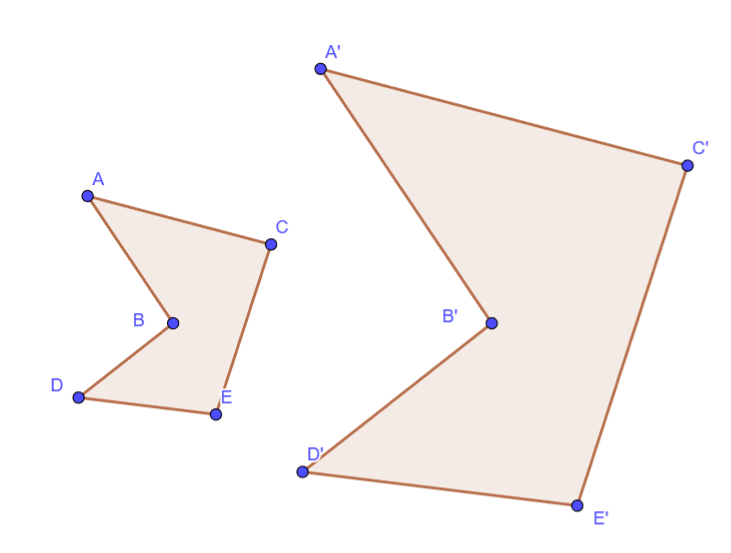
podemos estudiar si los triangulos que respectivamente lo componen son semejantes y estan puestos en el mismo orden.
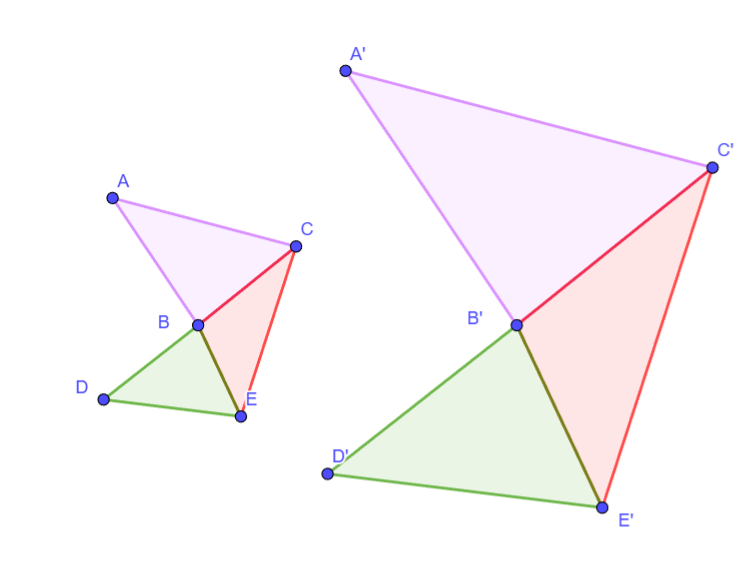
Semejanza de Figuras Irregulares (Planas):
Dos figuras planas irregulares son semejantes si una es una versión a escala de la otra. Como en estas figuras no siempre tenemos ángulos definidos para comparar, la condición de semejanza se basa en la proporcionalidad de las distancias. Para cualquier par de puntos correspondientes en las dos figuras, la razón entre sus distancias debe ser constante e igual a la razón de semejanza. Esta condición generaliza la idea de lados proporcionales en polígonos. Es necesario establecer una correspondencia clara entre los puntos de ambas figuras. Visualmente, deben tener la "misma forma", pero una puede ser más grande o más pequeña. Es importante destacar que todas las distancias correspondientes deben mantener la misma proporción para que la semejanza se cumpla.
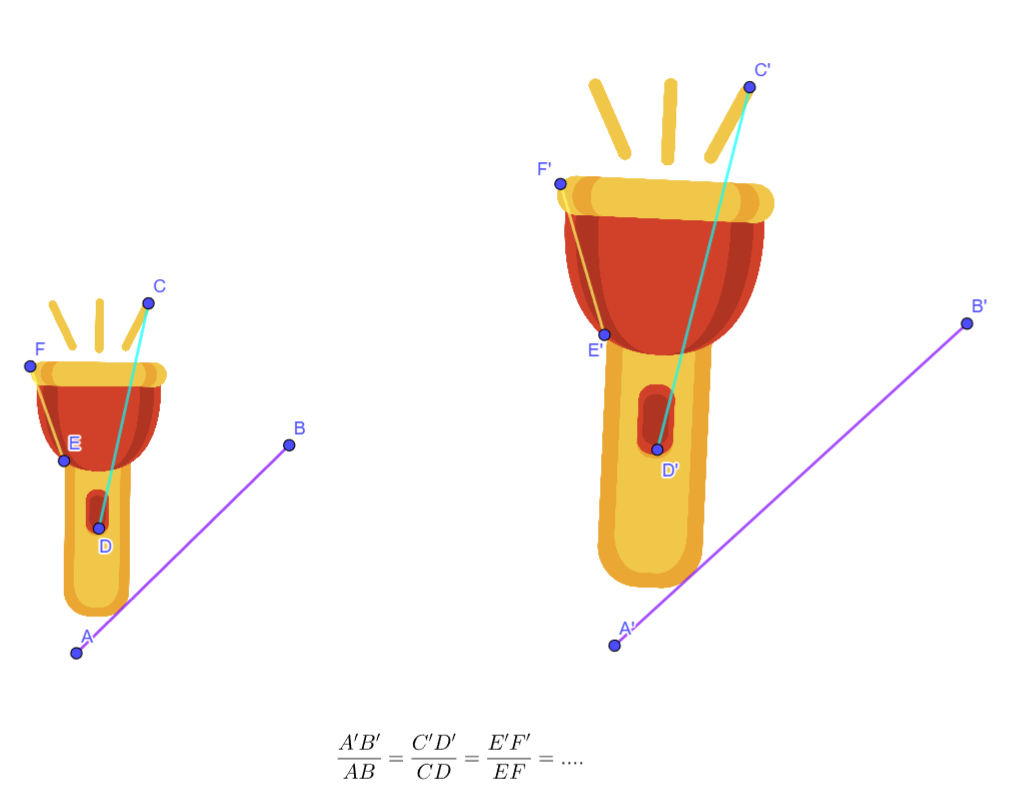
Aplicaciones:
La semejanza tiene numerosas aplicaciones prácticas, incluyendo:
- Cartografía: Mapas y planos a escala.
- Arquitectura y Diseño: Maquetas y modelos.
- Fotografía y Video: Ampliación y reducción de imágenes.
- Ingeniería: Construcción de modelos.
- Arte: Perspectiva.
- Diseño Gráfico
Conexión con Homotecias:
Recordemos que una transformación geométrica que produce figuras semejantes es la homotecia. La razón de semejanza entre dos figuras homotéticas es igual a la razón de la homotecia en el caso que dicha homotecia sea positiva.
Teorema de Tales:
Recordemos el Teorema de Tales, que establece que si tres o más rectas paralelas son intersectadas por dos transversales, entonces los segmentos determinados sobre las transversales son proporcionales. Aunque ya hemos demostrado este teorema, es importante destacar que también se puede demostrar utilizando el concepto de homotecia. Esta es una muestra más de la estrecha relación entre la semejanza y las homotecias.

