semejanzas y escalas
3. Razon de semejanza y razon de homotecia
Razón de Semejanza y Razón de Homotecia
Razón de Semejanza:
La razón de semejanza es la proporción constante entre las longitudes correspondientes de dos figuras semejantes. Es fundamental el orden en que se comparan las figuras:
- "Razón de semejanza de la figura S a la figura T":
- Significa que la figura T es la imagen (la figura transformada , ya sea ampliación o reduccion)
- La figura S es la preimagen (la figura original).
- La razón se calcula dividiendo una longitud en T (imagen) entre la longitud correspondiente en S (preimagen).
\[ \frac{imagen(T)}{preimagen(S)} \]
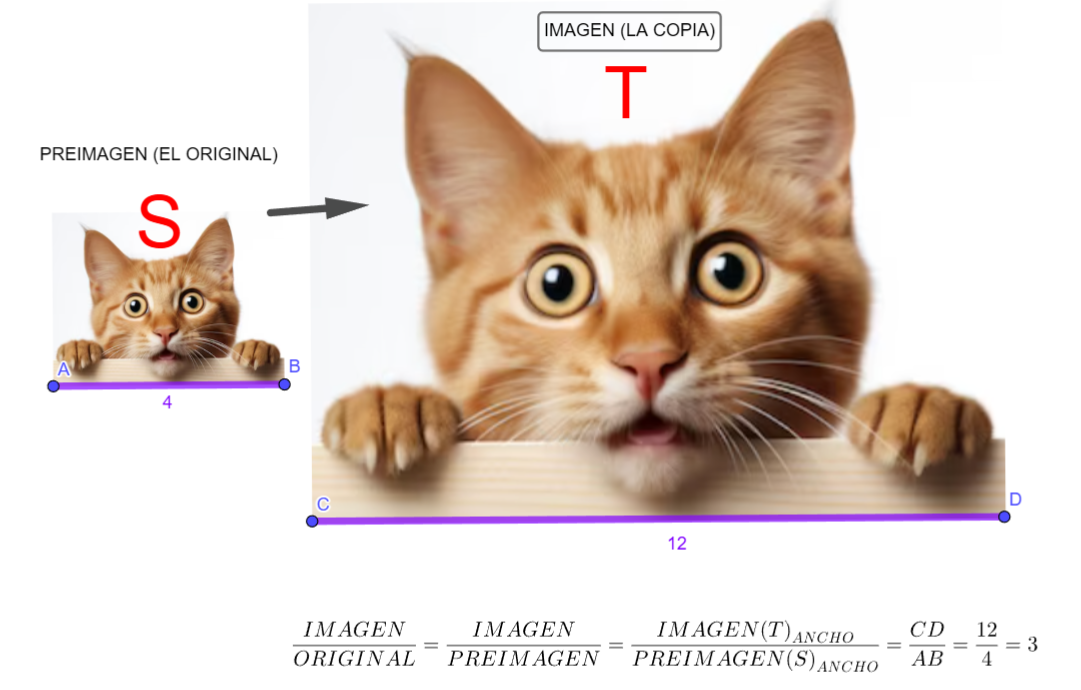
"Las medidas de la imagen son tres veces mas grande que las del original".
- "Razón de semejanza de la figura T a la figura S":
-
- Significa que la figura S es la imagen
- La figura T es la preimagen.
- La razón se calcula dividiendo una longitud en S (imagen) entre la longitud correspondiente en T (preimagen).
\[ \frac{imagen(S)}{original(T)} \]
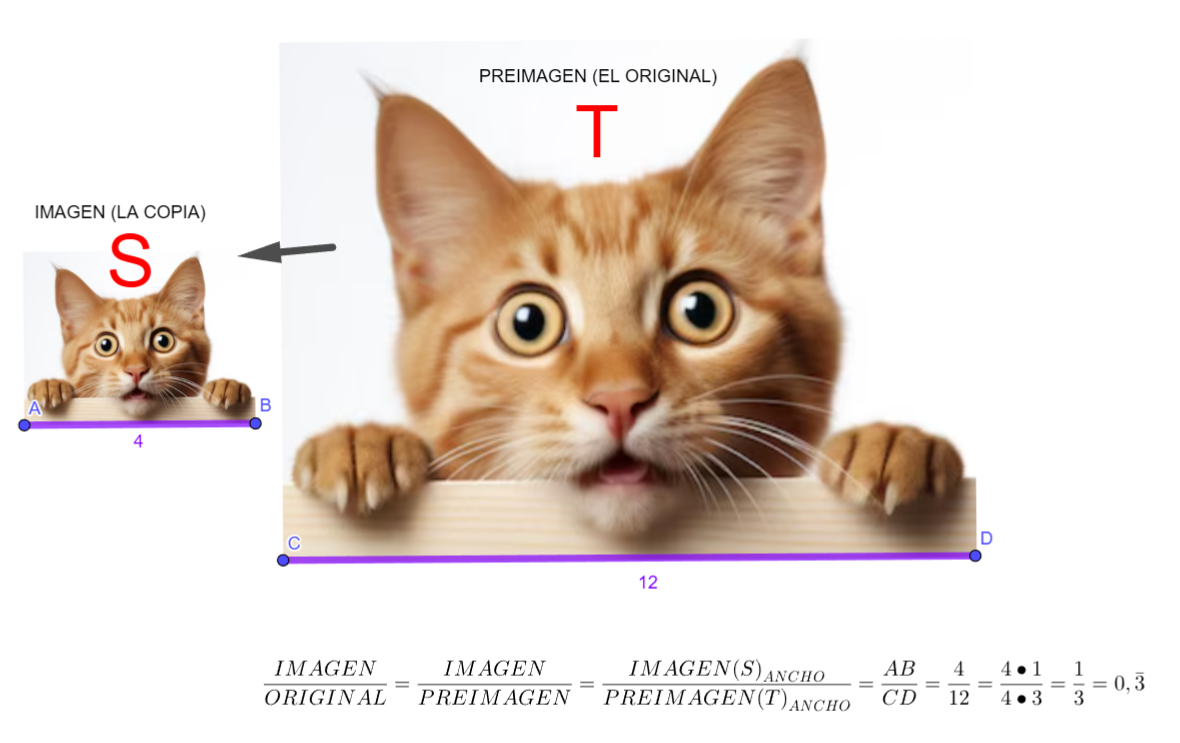
"Las medidas de la imagen son tres veces mas pequenas que las del original"
La razón de semejanza es siempre un número positivo, ya que representa una proporción entre longitudes. Si cambiamos el orden de la preimagen y la imagen, la razón de semejanza se invierte.
Ejemplo:
Sean dos triangulos ABC y A'B'C'
- El triángulo A'B'C' es semejante al triángulo ABC
- A'B' = 2 * AB,
Entonces:
- La razón de semejanza de ABC a A'B'C' es 2 (A'B'C' es el doble de grande).
- La razón de semejanza de A'B'C' a ABC es 1/2 (ABC es la mitad de grande).
Razón de Homotecia (k):
La razón de homotecia es el factor por el cual se multiplican las distancias desde un punto fijo (el centro de homotecia) para obtener una figura homotética. Indica:
- Magnitud del Escalamiento: El valor absoluto de k (|k|) determina el factor de escala.
- |k| > 1: Ampliación.
- 0 < |k| < 1: Reducción.
- |k| = 1: Congruencia.
- Dirección (Inversión): El signo de k:
- k > 0: La imagen está del mismo lado del centro de homotecia que la preimagen.
- k < 0: La imagen está del lado opuesto del centro (inversión).
Relación entre Razón de Semejanza y Razón de Homotecia:
Cuando dos figuras son homotéticas, la razón de semejanza entre ellas es igual al valor absoluto de la razón de homotecia (|k|). La homotecia garantiza la semejanza, y la razón de homotecia nos da, directamente (con su valor absoluto), la razón de semejanza.
Si dos figuras son simplemente semejantes, pero no sabemos si existe una homotecia que las relacione, solo podemos hablar de la razón de semejanza.
Ejemplos (Homotecia):
- k = 3: La figura homotética es tres veces más grande y está del mismo lado del centro. Razón de semejanza = 3.
- k = -1/2: La figura homotética es la mitad de grande y está invertida. Razón de semejanza = 1/2.
- k = -1: La figura homotética es una reflexión de la original. Razón de semejanza = 1.
En resumen: La razón de homotecia (k) describe completamente la transformación (escalamiento e inversión/dirección). La razón de semejanza, siempre positiva, solo indica la proporción entre los tamaños de las figuras, y es igual a |k| cuando las figuras son homotéticas. El orden en que se consideran la preimagen y la imagen es crucial para interpretar correctamente la razón de semejanza.
Ejercicios Conceptuales
- Verdadero o Falso (Justifica): "Si dos figuras son semejantes, entonces siempre son congruentes".
- Completar la frase: "La razón de semejanza de la figura A a la figura B es 3/4. Esto significa que la figura ________ es más grande, y cada longitud en la figura ___________ es _________ veces la longitud correspondiente en la figura ____________."
- Explicación: Dos amigos discuten. Uno dice que si dos rectángulos tienen todos sus ángulos iguales, entonces son semejantes. El otro dice que eso no es suficiente. ¿Quién tiene razón y por qué?
- Relación con Homotecia: Explica con tus propias palabras cómo se relacionan la razón de semejanza y la razón de homotecia cuando dos figuras son homotéticas. ¿Qué ocurre si la razón de homotecia es negativa?
Ejercicios Prácticos
- Dos triángulos, ABC y DEF, son semejantes. Se sabe que la razón de semejanza de ABC a DEF es 1/3. Si DE = 18 cm, calcula AB.
- En un triángulo rectángulo ABC, la altura desde el ángulo recto a la hipotenusa divide al triángulo en dos triángulos más pequeños. Demuestra que estos dos triángulos más pequeños son semejantes entre sí, y *determina la razón de semejanza entre ellos* si los segmentos en que la altura divide a la hipotenusa miden 4 cm y 9 cm.
- Dos triángulos, PQR y STU, son semejantes. La razón de semejanza de PQR a STU es 2/5. Si PQ = 6 cm, QR = 8 cm, y PR = 10 cm, calcula las longitudes de los lados de STU. *Expresa las longitudes de los lados de STU usando la razón de semejanza.*
- Dos pentágonos regulares son semejantes. Si la razón de semejanza del pentágono mayor al menor es 5/2, y el perímetro del pentágono menor es 30 cm, calcula la longitud del lado del pentágono mayor.
- Un arquitecto construye una maqueta de un edificio. La razón de semejanza de la maqueta al edificio real es 1/100. Si la altura de la maqueta es de 65 cm, ¿cuál es la altura real del edificio (en metros)? Si una ventana en el edificio real mide 2.5 metros de alto, ¿cuánto medirá la altura de la ventana correspondiente en la maqueta?
- Tienes una fotografía y la proyectas en una pantalla. La razón de semejanza de la imagen proyectada a la fotografía original es 5. Si el ancho de la fotografía original es de 12 cm, ¿cuál es el ancho de la imagen proyectada? Si quieres que la imagen proyectada tenga un ancho de 1.80 metros, ¿cuál debería ser la razón de semejanza entre la imagen proyectada y la fotografía original?
- Un árbol y un poste son perpendiculares al suelo. El árbol mide *h* metros y el poste 3 metros. En cierto momento del día, la razón de semejanza entre el triángulo formado por el árbol y su sombra y el triángulo formado por el poste y su sombra es 4. Si la sombra del poste mide 2.5 metros, ¿cuánto mide la sombra del árbol? ¿Cuánto mide el árbol?
- Se da un triangulo ABC, y un punto P. Se realiza una homotecia con centro en P. Dibuja una figura homotética A'B'C' si la razón de semejanza de A'B'C' a ABC es 3/2.
Problemas de Aplicación
- El telescopio casero: Quieres construir un telescopio casero... Si la distancia focal de la lente objetivo es 100 cm y la distancia focal de la lente ocular es 5 cm, ¿cuál es la *razón de semejanza* entre la imagen final que ves y el objeto real (muy lejano)?
- La cámara oscura: Una cámara oscura... Si un objeto de 1 metro de altura, situado a 5 metros del orificio, produce una imagen de 10 cm de altura en la pared opuesta, ¿cuál es la *razón de semejanza* entre la imagen y el objeto real? ¿A qué distancia está la pared opuesta del orificio?
- Estimación de alturas: Un método antiguo para estimar la altura de un árbol... Supón que tus ojos están a 1.60 metros del suelo. Te colocas a 2 metros de un espejo, y el espejo está a 15 metros del árbol. ¿Cuál es la *razón de semejanza* entre el triángulo formado por tu vista y el espejo y el triángulo formado por el árbol y el espejo? ¿Cuál es la altura del árbol?
- Diseño de una rampa: Quieres diseñar una rampa... Se te pide que la *razón de semejanza* entre el triángulo formado por la rampa y un triángulo más pequeño de referencia (con altura 1 metro y base 5 metros) sea de 1/4. ¿qué longitud tendrá la rampa resultante?

