Criterio AA de Semejanza de Triángulos

Enunciado

El criterio AA (Ángulo-Ángulo) establece que si dos ángulos de un triángulo son congruentes a dos ángulos de otro triángulo, entonces los dos triángulos son semejantes.

Si dos triangulos tienen dos ángulos correspondientes del mismo tamaño , es logico deducir que la tercera pareja de ángulos tambien serán congruentes ya que deben sumar 180°, por lo tanto los tres ángulos son congruentes

Pero ahora se debe deducir que los lados correspondientes seán proporcionales.... 

Demostración Formal

Dados dos triángulos, ΔABC y ΔDEF, donde ∠A ≅ ∠D y ∠B ≅ ∠E, demostraremos que ΔABC ~ ΔDEF.

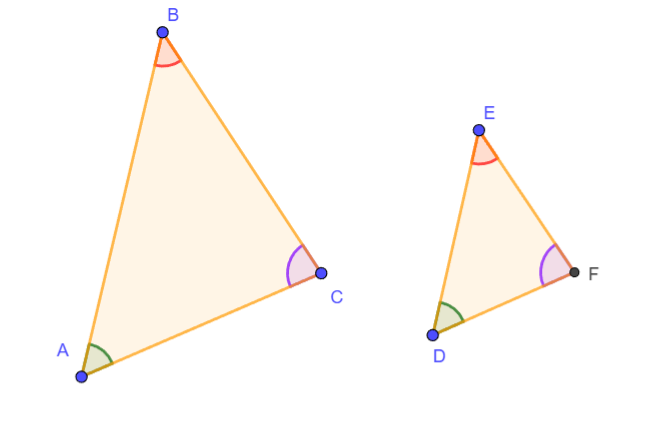
(Nota La siguiente demostracion supone que la primera figura es mas grande que la segunda, se podria extender los lados del primer triangulo en caso que el segundo sea mas grande y la demostracion seria valida igual, sin embargo para mayor claridad se eligio solo mostrar el primer caso "grande-chico" ya que el segundo seria trivialmente demostrable)

1.- Construcción: 

Con ayuda de un compaz Construimos un punto E' en AB  y F' en AC tal que DE = AE' y DF = AF'. Esto crea un triángulo ΔAE'F'.  

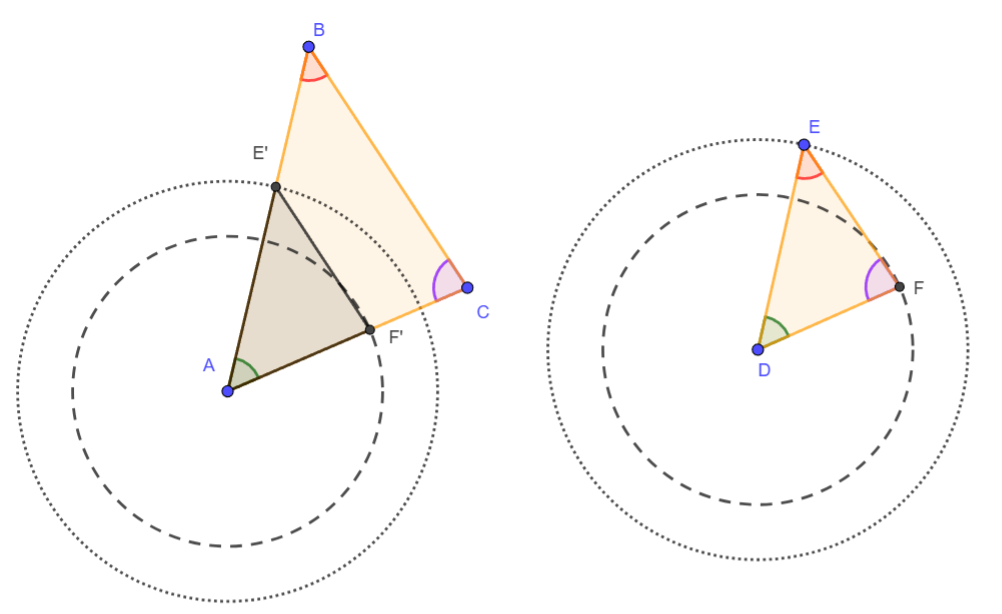
2.- Triángulos Congruentes: 

El triángulo que se formó es de la misma forma y tamaño que el segundo triángulo (el mas pequeño de ambos) y esto lo podemos asegurar por un criterio de congruencia LAL

" ΔAE'F' ≅ ΔDEF por el postulado LAL (Lado-Ángulo-Lado)".

3.- Ángulos Correspondientes:

podemos conliur entonces que  ∠E' ≅ ∠E (ángulos correspondientes de triángulos congruentes).

4.- Ángulos y Rectas Paralelas: 

 a)  ∠B ≅ ∠E (dado, es decir es premisa antes de empezar a demostrar) 
 b)  ∠E' ≅ ∠E (paso 3). 

Por transitividad, ∠B  ≅ ∠E', ya que ambos miden lo mismo (∠E )

 Al ser ∠B y ∠E' ángulos correspondientes (recordar secantes entre paralelas), podemos afirmar que  E'F' || BC.

5.- Usando el Teorema de Tales:

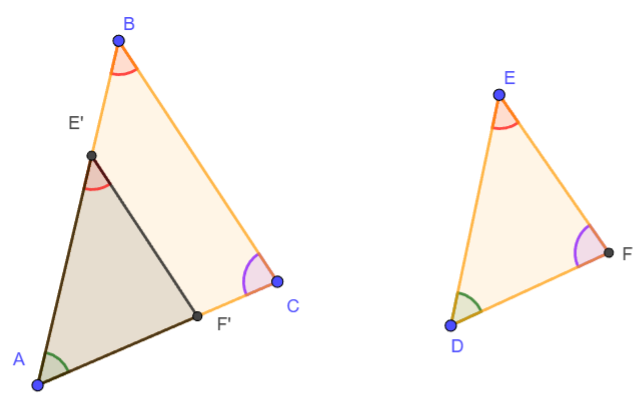
  Al ser E'F' || BC implica que
\[ \frac{AE'}{AB} = \frac{AF'}{AC} = \frac{E'F'}{BC} \]

6.- Sustitución:
Del paso 1 construcción sabiamos que AE' = DE y AF' = DF, asi que sustituyendo obtenemos

\[ \frac{DE}{AB} = \frac{DF}{AC} = \frac{E'F'}{BC} \]

Luego, como ΔAE'F' ≅ ΔDEF, E'F' = EF, por lo tanto: 

\[ \frac{DE}{AB} = \frac{DF}{AC} = \frac{EF}{BC} \]

Definición de Semejanza:
Los lados correspondientes son proporcionales.(recien demostrado)
los ángulos son congruentes (explicado al principio)
 entonces ΔABC ~ ΔDEF.


A continuación te presento La construccion que permite demostrar el criterio AA
puedes desplazar levemente los puntos para observar que la consistencia de dicha demostración es válida en todo tipo de triángulos

Ejemplos

Ejemplo 1: Triángulos Rectángulos

Dos triángulos rectángulos con un ángulo agudo de 30° son semejantes por AA (90° y 30°).

Ejemplo 2: Triángulos con Ángulos Compartidos

Un triángulo grande ΔABC y un triángulo más pequeño ΔADE (con DE || BC) son semejantes por AA (∠A compartido y ángulos correspondientes).

Ejemplo 3: Medición Indirecta

Si una vara de altura 'v' proyecta una sombra 's', y un edificio proyecta una sombra 'S', la altura del edificio 'H' se puede calcular como H = (v * S) / s, usando triángulos semejantes formados por la vara, el edificio y sus sombras.