Criterio LAL de Semejanza de Triángulos

Enunciado

El criterio LAL (Lado-Ángulo-Lado) establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo, y los ángulos comprendidos entre esos lados son congruentes, entonces los dos triángulos son semejantes.

Es decir, si tenemos dos triángulos, \( \triangle ABC \) y \( \triangle DEF \), y podemos verificar que \( \frac{AB}{DE} = \frac{AC}{DF} \) (es decir, que los lados \( AB \) y \( AC \) del primer triángulo son proporcionales a los lados \( DE \) y \( DF \) del segundo triángulo, respectivamente), y además, \( \angle A \cong \angle D \) (el ángulo entre \( AB \) y \( AC \) es congruente al ángulo entre \( DE \) y \( DF \)), entonces \( \triangle ABC \sim \triangle DEF \).

Demostración Formal

Dados dos triángulos, \( \triangle ABC \) y \( \triangle DEF \), donde \( \frac{AB}{DE} = \frac{AC}{DF} \) y \( \angle A \cong \angle D \), demostraremos que \( \triangle ABC \sim \triangle DEF \).

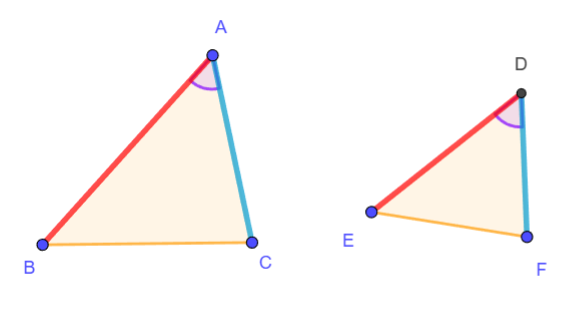
(Nota: Asumiremos, para simplificar la visualización, que \( \triangle ABC \) es mayor que \( \triangle DEF \). La demostración se puede adaptar fácilmente al caso contrario.)

Construcción:

Con ayuda de una regla, construimos un punto \( E' \) en \( AB \) tal que \( AE' = DE \). Luego, trazamos un segmento \( E'F' \) paralelo a \( BC \), donde \( F' \) está en \( AC \). Esto crea un triángulo \( \triangle AE'F' \).

Proporcionalidad (Teorema de Tales):

Como \( E'F' \parallel BC \), por el Teorema de Tales, sabemos que:

\[ \frac{AB}{AE'} = \frac{AC}{AF'} \]

Sustitución (usando la hipótesis):

Sabemos (por construcción) que \(AE' = DE\). También sabemos que \(\frac{AB}{DE} = \frac{AC}{DF}\). Podemos expresar esto como \(\frac{DE}{AB}=\frac{DF}{AC}\).

Sustituyendo \( AE' \) por \( DE \) en la proporción anterior:

\[ \frac{AB}{DE} = \frac{AC}{AF'} \]

Como \(\frac{DE}{AB} = \frac{DF}{AC}\), entonces, por transitividad:

\[ \frac{AC}{AF'} = \frac{AC}{DF} \]

Esto implica que \( AF' = DF \).

Triángulos Congruentes:

Ahora tenemos:

• \( AE' = DE \) (por construcción)
• \( AF' = DF \) (demostrado)
• \( \angle A \cong \angle D \) (dado)

Por el postulado LAL de congruencia de triángulos, podemos afirmar que \( \triangle AE'F' \cong \triangle DEF \).

Ángulos Correspondientes y Semejanza:

Como \( \triangle AE'F' \cong \triangle DEF \), sabemos que todos sus ángulos correspondientes son congruentes. En particular, \( \angle AE'F' \cong \angle E \).

Además, por construcción, como \(E'F' \parallel BC\), se tiene que \( \angle AE'F' \cong \angle B\)

Por transitividad, \( \angle B \cong \angle E \).

Ahora, en los triángulos originales \( \triangle ABC \) y \( \triangle DEF \), tenemos:

• \( \angle A \cong \angle D \) (dado)
• \( \angle B \cong \angle E \) (demostrado)

Por el criterio AA de semejanza, concluimos que \( \triangle ABC \sim \triangle DEF \).

En resumen:

Hemos construido un triángulo (\( \triangle AE'F' \)) congruente al triángulo más pequeño (\( \triangle DEF \)) dentro del triángulo más grande (\( \triangle ABC \)). Usando la proporcionalidad dada y el Teorema de Tales, demostramos que los lados del triángulo construido son proporcionales a los lados del triángulo grande. Finalmente, la congruencia de ángulos y el criterio AA nos permiten concluir que los dos triángulos originales son semejantes. ¡Hemos demostrado el criterio LAL!