Los números naturales
8. ¡Explorando el Mundo de los Números Primos!
¡Explorando el Mundo de los Números Primos!
Imagina que los números son como bloques de construcción. ¡Algunos son piezas únicas y fundamentales! Esos bloques especiales se llaman números primos.
- Un número primo es un número natural mayor que 1 que solo tiene dos divisores distintos: el 1 y sí mismo. (Ej: 2, 3, 5, 7, 11)
- Un número compuesto es aquel que tiene más de dos divisores. (Ej: 4, 6, 8, 9, 10)
- Ojo: El número 1 no se considera ni primo ni compuesto.
Ejemplos para entender la diferencia
La clave está en contar cuántos divisores tiene un número. Usemos tu idea de los "divisores elementales" (que son siempre el 1 y el mismo número).
| ✅ Números Primos (Solo 2 divisores) | ❌ Números Compuestos (Más de 2 divisores) |
|---|---|
| Número 7 Divisores: {1, 7} Tiene solo los 2 divisores elementales. |
Número 9 Divisores: {1, 3, 9} Tiene los 2 elementales y otros más (en este caso, el 3). |
| Número 11 Divisores: {1, 11} Tiene solo los 2 divisores elementales. |
Número 12 Divisores: {1, 2, 3, 4, 6, 12} Tiene los 2 elementales y muchos otros más. |
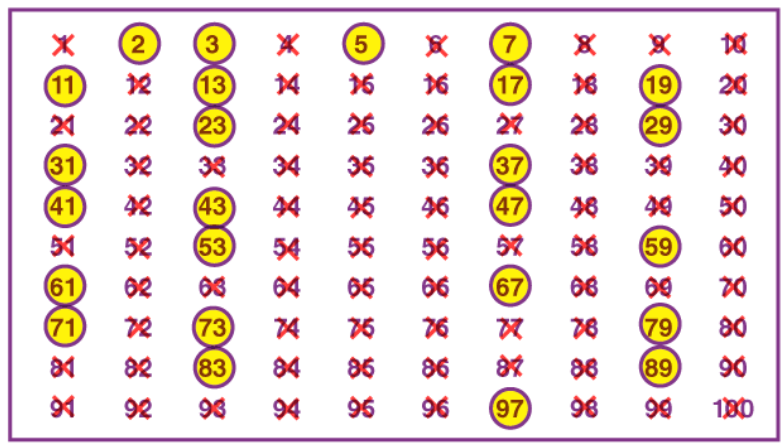
¡A cazar primos con la Criba de Eratóstenes!
La Criba de Eratóstenes es un método antiguo y muy visual para encontrar todos los números primos hasta un cierto límite. ¡Es como un juego de detectives!
- Escribe una lista de números, por ejemplo, del 1 al 50.
- Tacha el número 1, ya que no es primo.
- Encierra en un círculo el 2 (el primer primo) y tacha todos sus múltiplos (4, 6, 8...).
- Encierra el siguiente número no tachado (el 3) y tacha todos sus múltiplos (6, 9, 12...).
- Continúa este proceso hasta que todos los números estén encerrados o tachados.
Al final, ¡todos los números que quedaron encerrados son los primos!
Descomposición en Factores Primos
Los números primos son los "ladrillos" con los que se construyen todos los demás números. Cualquier número compuesto puede escribirse como un producto único de números primos. A esto se le llama descomposición o factorización prima.
Ejemplo: Descomponer el número 36
Podemos hacerlo con divisiones sucesivas:
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
Entonces, la descomposición prima de 36 es: 2 x 2 x 3 x 3, que se escribe como \(2^2 \times 3^2\).
También podemos usar un árbol de factores:
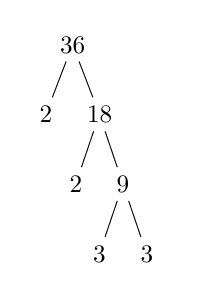
¡Practica la factorización!
Ahora es tu turno. Intenta descomponer los siguientes números en factores primos:
- 48
- 75
- 120
- 160
- 392
- 48 = \(2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3\)
- 75 = \(3 \times 5 \times 5 = 3 \times 5^2\)
- 120 = \(2 \times 2 \times 2 \times 3 \times 5 = 2^3 \times 3 \times 5\)
- 160 = \(2 \times 2 \times 2 \times 2 \times 2 \times 5 = 2^5 \times 5\)
- 392 = \(2 \times 2 \times 2 \times 7 \times 7 = 2^3 \times 7^2\)
¿Por qué son importantes los números primos?
- Son los "ladrillos" de los números: Todo número compuesto tiene una "receta" única de factores primos (Teorema Fundamental de la Aritmética).
- Simplificación de fracciones: Conocer los factores primos de numerador y denominador es la clave para simplificar fracciones de forma eficiente.
- Criptografía: La seguridad en internet (contraseñas, transacciones bancarias) depende de operaciones con números primos extremadamente grandes.
Cuando envías un mensaje por WhatsApp o compras algo online, tu información se protege usando un sistema de llaves (pública y privada). La seguridad de este sistema se basa en que es muy fácil multiplicar dos números primos gigantes, pero es extremadamente difícil tomar el resultado (un número compuesto muy grande) y descubrir cuáles fueron los dos primos originales que lo formaron. ¡Las matemáticas protegen tus secretos!

