4. Operaciones con Números Enteros: Suma y Resta

Operaciones con Números Enteros: Suma y Resta

🌍 Entendiendo los Números Enteros con Dinero

Imagina que el dinero que tienes en tu bolsillo son números positivos y el dinero que debes son números negativos. Esta es una forma simple de ver cómo funcionan:

  • Si tienes $5 y recibes $3 más: \(5 + 3 = 8\). Ahora tienes $8.
  • Si debes $4 y pides prestado $2 más: \((-4) + (-2) = -6\). Ahora tu deuda total es de $6.
  • Si debes $7 pero solo tienes $5: \((-7) + 5 = -2\). Después de pagar, todavía debes $2.
  • Si tienes $8 y pagas una deuda de $3: \(8 + (-3) = 5\). Después de pagar, te quedan $5.

Suma de Números Enteros

📐 Reglas para Sumar Enteros

1. Números con el mismo signo: Se suman sus valores y se mantiene el mismo signo.

  • \(3 + 5 = 8\)
  • \((-4) + (-2) = -6\)

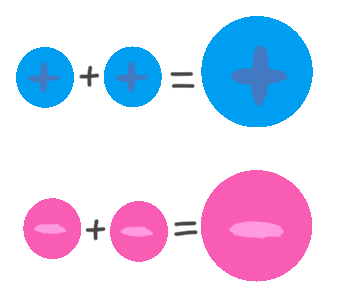
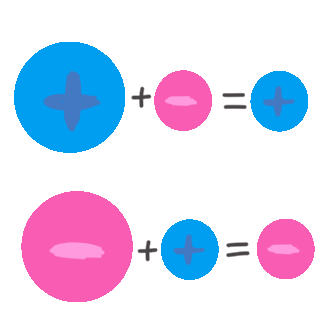
2. Números con distinto signo: Se restan sus valores (el mayor menos el menor) y el resultado se queda con el signo del número que tiene mayor valor.

  • \(7 + (-2) = 5\) (El 7 es más grande, el resultado es positivo)
  • \((-8) + 3 = -5\) (El 8 es más grande, el resultado es negativo)

🤓 Visualizando la Suma en la Recta Numérica

Usar la recta numérica es una excelente estrategia visual para entender cómo se comportan los números enteros. La regla de oro es:

  • Sumar un número positivo significa moverse hacia la derecha (en la dirección de los números más grandes).
  • Sumar un número negativo significa moverse hacia la izquierda (en la dirección de los números más pequeños).

Veamos los cuatro casos posibles:

Caso 1: Positivo + Positivo (Ejemplo: \(3 + 2\))

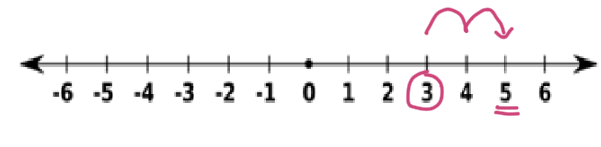
Partimos del 3 y, como sumamos un número positivo (2), nos movemos 2 unidades a la derecha. ¡Llegamos al 5!

Suma de 3 + 2 en la recta numérica

Caso 2: Negativo + Negativo (Ejemplo: \((-4) + (-1)\))

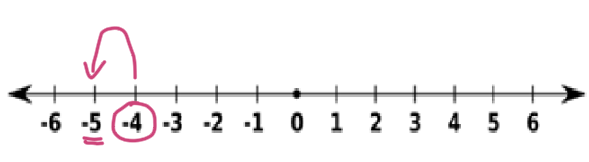
Partimos del -4 y, como sumamos un número negativo (-1), nos movemos 1 unidad a la izquierda. ¡Llegamos al -5!

Suma de -4 + (-1) en la recta numérica

Caso 3: Positivo + Negativo (Ejemplo: \(5 + (-3)\))

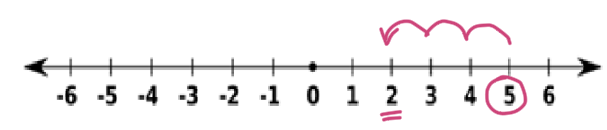
Partimos del 5 y, como sumamos un número negativo (-3), nos movemos 3 unidades a la izquierda. ¡Llegamos al 2!

Suma de 5 + (-3) en la recta numérica

Caso 4: Negativo + Positivo (Ejemplo: \((-2) + 6\))

Partimos del -2 y, como sumamos un número positivo (6), nos movemos 6 unidades a la derecha. ¡Llegamos al 4!

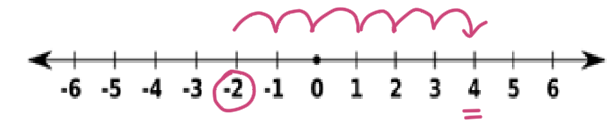
Suma de -2 + 6 en la recta numérica

Resta de Números Enteros

💡 Idea Clave: Transformar la Resta en Suma

Restar un número entero es exactamente lo mismo que sumar su número opuesto. Este truco simplifica todas las restas.

Por ejemplo: \(5 - 3\) se convierte en \(5 + (-3)\).

⚠️ ¡Advertencia! Cuidado al restar un negativo

Este es un error muy común. Restar un número negativo es sumar su opuesto positivo. ¡Los dos signos "menos" seguidos se convierten en un "más"!

Ejemplo: \(4 - (-1)\) se transforma en \(4 + 1 = 5\).

Ejemplo: Restar es lo mismo que sumar el opuesto

Esta es una regla fundamental. En vez de pensar en restar, siempre puedes transformarlo en una suma, lo que a menudo es más fácil. Simplemente sumas el número opuesto.

Observa los siguientes casos:

  • \( 5 - 3 \) se convierte en \( 5 + (-3) = 2 \)
  • \( -2 - 6 \) se convierte en \( -2 + (-6) = -8 \)
  • \( 4 - (-1) \) se convierte en \( 4 + 1 = 5 \)
  • \( -7 - (-3) \) se convierte en \( -7 + 3 = -4 \)
💡 Estrategias para Operaciones Combinadas

Cuando te enfrentas a una cadena de sumas y restas, existen dos métodos muy efectivos para llegar al resultado. ¡Puedes elegir el que más te acomode!

  • Método 1 (Directo): Operar de izquierda a derecha, paso a paso.
  • Método 2 (Agrupar): Juntar todos los números positivos, luego todos los negativos, y al final resolver la operación entre ambos grupos.
Ejemplo 1: Resolviendo \( 2 + (-5) - (-3) + 1 - 4 \)

Paso 1: Convertir todas las restas en sumas del opuesto.
La expresión se transforma en: \( 2 + (-5) + 3 + 1 + (-4) \)

Paso 2 (Método Directo):
\( 2 + (-5) = -3 \)
\( -3 + 3 = 0 \)
\( 0 + 1 = 1 \)
\( 1 + (-4) = -3 \)

Paso 2 (Método de Agrupar):
Positivos: \( 2 + 3 + 1 = 6 \)
Negativos: \( (-5) + (-4) = -9 \)
Resultado: \( 6 + (-9) = -3 \)

Resultado Final: -3

Ejemplo 2: Resolviendo \( -6 - 2 + (-1) - (-7) + 4 \)

Paso 1: Convertir todas las restas en sumas del opuesto.
La expresión se transforma en: \( -6 + (-2) + (-1) + 7 + 4 \)

Paso 2 (Método Directo):
\( -6 + (-2) = -8 \)
\( -8 + (-1) = -9 \)
\( -9 + 7 = -2 \)
\( -2 + 4 = 2 \)

Paso 2 (Método de Agrupar):
Positivos: \( 7 + 4 = 11 \)
Negativos: \( (-6) + (-2) + (-1) = -9 \)
Resultado: \( 11 + (-9) = 2 \)

Resultado Final: 2

📝 Práctica Guiada: Suma y Resta de Enteros

Estos ejercicios están organizados en 5 niveles. Resuelve cada nivel y luego presiona su respectivo botón para ver las soluciones.

Nivel 1: Suma de Números Positivos

  1. \( (+7) + (+3) = \)
  2. \( (+9) + (+8) = \)
  3. \( (+2) + (+6) + (+4) = \)
  4. \( (+5) + (+1) + (+9) = \)
  5. \( 11 + 4 = \)
  6. \( 15 + 8 = \)
  7. \( 20 + 12 = \)
  8. \( 3 + 6 + 9 = \)
  9. \( 10 + 20 + 5 = \)
  10. \( 7 + 2 + 11 = \)

Nivel 2: Suma de Números Negativos

  1. \( (-5) + (-4) = \)
  2. \( (-8) + (-6) = \)
  3. \( (-10) + (-2) = \)
  4. \( (-15) + (-5) = \)
  5. \( (-1) + (-9) = \)
  6. \( (-2) + (-3) + (-4) = \)
  7. \( (-7) + (-1) + (-2) = \)
  8. \( (-5) + (-5) + (-5) = \)
  9. \( (-10) + (-20) + (-30) = \)
  10. \( (-8) + (-2) + (-10) = \)

Nivel 3: Suma con Signos Mixtos

  1. \( 12 + (-5) = \)
  2. \( 8 + (-10) = \)
  3. \( 20 + (-25) = \)
  4. \( (-7) + 3 = \)
  5. \( (-15) + 20 = \)
  6. \( (-9) + 9 = \)
  7. \( 6 + (-10) + 2 = \)
  8. \( (-8) + 12 + (-3) = \)
  9. \( 20 + (-5) + (-15) = \)
  10. \( -3 + 13 + (-10) = \)

Nivel 4: Resta de Números Enteros

Recuerda la idea clave: restar un número es lo mismo que sumar su opuesto.

  1. \( 20 - 8 = \)
  2. \( 10 - 17 = \)
  3. \( 30 - (+10) = \)
  4. \( -15 - 5 = \)
  5. \( -9 - 11 = \)
  6. \( (-7) - (+8) = \)
  7. \( 14 - (-6) = \)
  8. \( 10 - (-10) = \)
  9. \( 5 - (-15) = \)
  10. \( (-8) - (-5) = \)
  11. \( (-12) - (-20) = \)
  12. \( (-9) - (-9) = \)

Nivel 5: Operaciones Combinadas

Usa la estrategia que más te acomode: operar de izquierda a derecha o agrupar.

  1. \( 8 - 10 + 3 = \)
  2. \( -5 - 4 + 12 = \)
  3. \( 10 + (-5) - 6 = \)
  4. \( 15 - 20 + 5 - 1 = \)
  5. \( -7 - 3 + 10 - 2 = \)
  6. \( 20 - (-10) - 5 = \)
  7. \( -8 - (-4) + (-5) = \)
  8. \( 14 - 9 - (-2) + 1 = \)
  9. \( -3 + (-7) - (-10) + 1 = \)
  10. \( 30 - 40 + (-5) - (-15) = \)

Encuentra el Sumando Faltante

1. \(4 + \_\_\_ = 1\)

2. \(\_\_\_ + (-3) = -8\)

3. \(-2 + \_\_\_ = 5\)

4. \(\_\_\_ + 7 = 0\)

5. \(-9 + \_\_\_ = -4\)

6. \(\_\_\_ + (-1) = -1\)

Problemas con Números Enteros

1. La temperatura en la mañana era de -3°C. Al mediodía, la temperatura subió 8°C. Por la noche, bajó 5°C. ¿Cuál fue la temperatura al final del día?

2. Un submarino se encuentra a -120 metros (120 metros bajo el nivel del mar). Primero, asciende 40 metros. Luego, desciende 65 metros. ¿A qué profundidad se encuentra el submarino finalmente?

3. Ana tenía $50 en su cuenta bancaria. Hizo un retiro de $80, luego depositó $35 y finalmente hizo otro retiro de $20. ¿Cuál es el saldo de su cuenta?

4. En un juego, Juan avanzó 5 pasos, retrocedió 9 pasos, luego avanzó 3 pasos y finalmente retrocedió 2 pasos. ¿Cuál es su posición final respecto al punto de inicio?

5. Un ascensor se encuentra en el piso 3. Sube 5 pisos, luego baja 9 pisos, sube 2 pisos y finalmente baja 6 pisos. ¿En qué piso se encuentra el ascensor al final?

¡Practica con estos ejercicios y verás cómo dominas la suma y la resta de números enteros!