Capitulo 0.2 N° enteros (nivelacion)
5. Problemas de Variación con Números Enteros
Problemas de Variación con Números Enteros
En este tipo de problemas, nos interesa encontrar la diferencia entre dos valores. Esta diferencia nos muestra cómo ha cambiado una cantidad, ya sea aumentando (variación positiva) o disminuyendo (variación negativa).
Para encontrar la diferencia o variación entre dos números enteros, siempre usamos la misma fórmula:
Variación = Valor Final - Valor Inicial
- Un resultado positivo indica un aumento o incremento.
- Un resultado negativo indica una disminución o decremento.
Ejemplos Resueltos
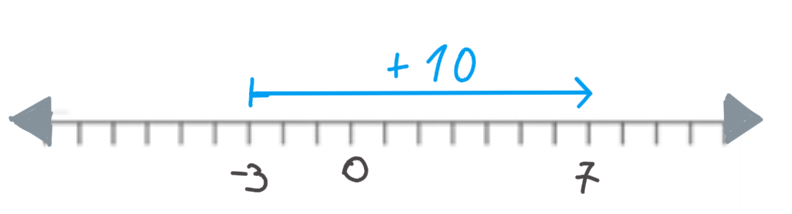
Problema: La temperatura a las 8:00 AM era de -3°C y a las 12:00 PM era de 7°C. ¿Cuál fue la variación de temperatura?
- Valor final: 7°C
- Valor inicial: -3°C
Operación: \( 7 - (-3) = 7 + 3 = 10 \)
Respuesta: La variación de temperatura fue de 10°C (un aumento de 10°C).
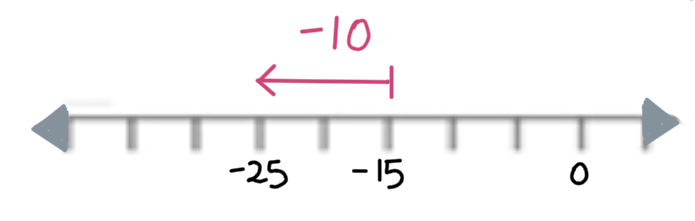
Problema: Un buzo se encontraba a -15 metros y descendió hasta -25 metros. ¿Cuál fue la variación en su altitud?
- Valor final: -25 m
- Valor inicial: -15 m
Operación: \( -25 - (-15) = -25 + 15 = -10 \)
Respuesta: La variación en su altitud fue de -10 metros (un descenso de 10 metros).
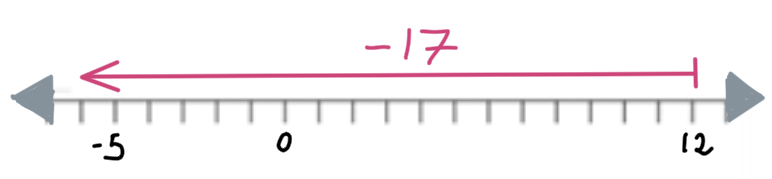
Problema: Ana tenía $12 en su cuenta y luego de una transacción, su saldo quedó en -$5 (debe $5). ¿Cuál fue la variación en su saldo?
- Valor final: -$5
- Valor inicial: $12
Operación: \( -5 - 12 = -17 \)
Respuesta: La variación en el saldo fue de -$17 (una disminución de $17).
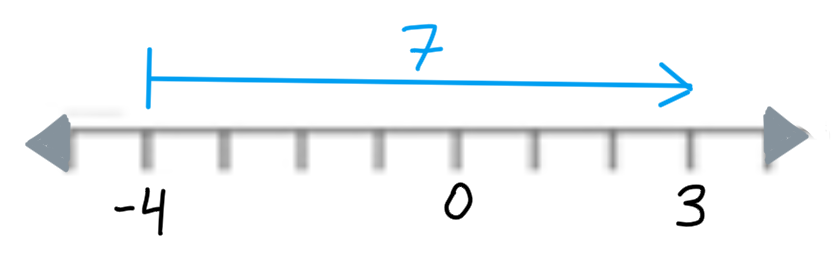
Problema: Un objeto se mueve desde la posición -4 en una recta numérica hasta la posición 3. ¿Cuál fue la variación en su posición?
- Valor final: 3
- Valor inicial: -4
Operación: \( 3 - (-4) = 3 + 4 = 7 \)
Respuesta: La variación en su posición fue de 7 (un desplazamiento de 7 unidades a la derecha).
En el lenguaje común, a veces usamos la palabra "diferencia" para referirnos a qué tan lejos están dos números, sin importar el orden. Sin embargo, en matemática y ciencias, la variación es un concepto preciso que nos indica tanto la magnitud como la dirección del cambio.
Por ejemplo, si la temperatura baja de 8°C a 2°C:
- Alguien podría decir que la "diferencia" es de 6°C. Este número es correcto en magnitud, pero no nos dice si la temperatura subió o bajó.
- La variación se calcula siempre como Valor Final - Valor Inicial. En este caso, es \( 2 - 8 = -6°C \). El signo negativo es fundamental, ya que nos confirma que la temperatura disminuyó.
Para estos problemas, ¡recuerda siempre usar la fórmula de variación para obtener la historia completa!
Ejercicios de Práctica
- La temperatura en la mañana era de 2°C y en la tarde era de -1°C. ¿Cuál fue la variación de temperatura?
- Un submarino estaba a -180 metros y ascendió a -120 metros. ¿Cuál fue la variación en su profundidad?
- Juan tenía una deuda de $25 (-$25) y luego de hacer un pago, su deuda quedó en $10 (-$10). ¿Cuál fue la variación en su saldo?
- Un ascensor estaba en el piso 8 y bajó al piso -1 (primer sótano). ¿Cuál fue la variación en su posición?
- En un juego, un jugador tenía -7 puntos y luego obtuvo 15 puntos. ¿Cuál fue la variación en su puntaje?
- Un auto se mueve de la posición 5 a la posición -2 en una carretera recta. ¿Cuál fue la variación en su posición?
- La temperatura al inicio de un experimento era de -5°C y al final era de -12°C. ¿Cuál fue la variación de temperatura?
Respuestas:
- Variación: \( (-1) - 2 = -3 \). La temperatura bajó 3°C.
- Variación: \( (-120) - (-180) = 60 \). El submarino subió 60 metros.
- Variación: \( (-10) - (-25) = 15 \). El saldo de Juan aumentó en $15 (su deuda disminuyó).
- Variación: \( (-1) - 8 = -9 \). El ascensor bajó 9 pisos.
- Variación: \( 15 - (-7) = 22 \). El puntaje aumentó en 22 puntos.
- Variación: \( (-2) - 5 = -7 \). El auto se desplazó 7 unidades en sentido negativo.
- Variación: \( (-12) - (-5) = -7 \). La temperatura bajó 7°C.

