Libro Productos Notables
2. El Cuadrado de un Binomio: el caso de la suma
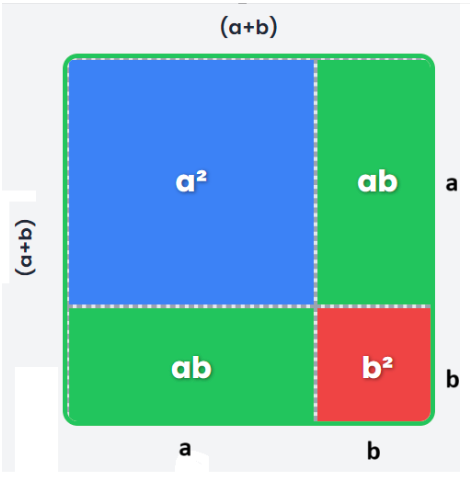
Ahora que hemos repasado la propiedad distributiva, estamos listos para explorar uno de los productos notables más importantes: el cuadrado de un binomio. En esta página nos enfocaremos en el caso de la suma, es decir, expresiones de la forma \((a+b)^2\).
Desarrollo del Producto Notable \((a+b)^2\)
¿Qué significa elevar un binomio al cuadrado?
Elevar un binomio al cuadrado significa multiplicarlo por sí mismo. Entonces:
\[ (a+b)^2=(a+b)(a+b) \]
Usando la propiedad distributiva:
\[ (a+b)(a+b)=a(a+b)+b(a+b) \]
\[ =a^2+ab+ba+b^2 \]
Como \(ab\) y \(ba\) representan el mismo producto, se suman:
\[ a^2+ab+ba+b^2=a^2+2ab+b^2 \]
Fórmula del cuadrado de un binomio suma
El desarrollo de un cuadrado de binomio suma siempre sigue este patrón:
\[ (a+b)^2=a^2+2ab+b^2 \]
Se lee: el primer término al cuadrado, más el doble del producto del primer término por el segundo, más el segundo término al cuadrado.
Ejemplo visual
El área total de un cuadrado de lado \(a+b\) se puede dividir en cuatro partes: una de área \(a^2\), dos rectángulos de área \(ab\), y una de área \(b^2\). Por eso:
\[ (a+b)^2=a^2+ab+ab+b^2=a^2+2ab+b^2 \]
Ejercicios: cuadrado de un binomio suma
Ejemplo guiado: nivel 1
Resolvamos \((4+2)^2\) usando la fórmula.
Identificamos \(a=4\) y \(b=2\).
Aplicamos:
\[ (a+b)^2=a^2+2ab+b^2 \]
\[ (4+2)^2=4^2+2\cdot 4\cdot 2+2^2 \]
\[ =16+16+4=36 \]
Comprobación:
\[ (4+2)^2=6^2=36 \]
Nivel 1: expandir con valores enteros
- \((2+3)^2\)
- \((5+1)^2\)
- \((4+6)^2\)
- \((7+2)^2\)
1. \[ (2+3)^2=2^2+2\cdot 2\cdot 3+3^2=4+12+9=25 \]
2. \[ (5+1)^2=5^2+2\cdot 5\cdot 1+1^2=25+10+1=36 \]
3. \[ (4+6)^2=4^2+2\cdot 4\cdot 6+6^2=16+48+36=100 \]
4. \[ (7+2)^2=7^2+2\cdot 7\cdot 2+2^2=49+28+4=81 \]
Ejemplo guiado: nivel 2
Resolvamos \((1{,}5+0{,}5)^2\) usando la fórmula.
Identificamos \(a=1{,}5\) y \(b=0{,}5\).
\[ (1{,}5+0{,}5)^2=(1{,}5)^2+2(1{,}5)(0{,}5)+(0{,}5)^2 \]
\[ =2{,}25+1{,}5+0{,}25=4 \]
Comprobación:
\[ (1{,}5+0{,}5)^2=2^2=4 \]
Nivel 2: expandir con valores racionales
- \((0{,}5+1)^2\)
- \(\left(\frac{1}{2}+\frac{1}{4}\right)^2\)
- \(\left(2+1\frac{1}{2}\right)^2\)
- \((1{,}2+0{,}8)^2\)
1. \[ (0{,}5+1)^2=(0{,}5)^2+2(0{,}5)(1)+1^2 \]
\[ =0{,}25+1+1=2{,}25 \]
2. \[ \left(\frac{1}{2}+\frac{1}{4}\right)^2= \left(\frac{1}{2}\right)^2+ 2\left(\frac{1}{2}\right)\left(\frac{1}{4}\right)+ \left(\frac{1}{4}\right)^2 \]
\[ =\frac{1}{4}+\frac{1}{4}+\frac{1}{16} =\frac{4}{16}+\frac{4}{16}+\frac{1}{16} =\frac{9}{16} \]
3. Primero escribimos \(1\frac{1}{2}=\frac{3}{2}\):
\[ \left(2+\frac{3}{2}\right)^2= 2^2+2\cdot 2\cdot \frac{3}{2}+\left(\frac{3}{2}\right)^2 \]
\[ =4+6+\frac{9}{4} =10+\frac{9}{4} =\frac{49}{4}=12{,}25 \]
4. \[ (1{,}2+0{,}8)^2=(1{,}2)^2+2(1{,}2)(0{,}8)+(0{,}8)^2 \]
\[ =1{,}44+1{,}92+0{,}64=4 \]
Ejemplo guiado: nivel 3
Expandamos \((3x+2y)^2\).
Identificamos \(a=3x\) y \(b=2y\).
Primer término al cuadrado:
\[ (3x)^2=9x^2 \]
Doble producto del primero por el segundo:
\[ 2(3x)(2y)=12xy \]
Segundo término al cuadrado:
\[ (2y)^2=4y^2 \]
Resultado:
\[ (3x+2y)^2=9x^2+12xy+4y^2 \]
Nivel 3: expandir con expresiones algebraicas
- \((x+2)^2\)
- \((3+a)^2\)
- \((m+n)^2\)
- \((2x+1)^2\)
- \((4+3y)^2\)
- \(\left(\frac{1}{2}a+2\right)^2\)
- \((0{,}5x+1{,}5)^2\)
- \((x+y)^2\)
- \((2a+3b)^2\)
- \(\left(m+\frac{1}{3}\right)^2\)
- \((2{,}5+x)^2\)
- \((3x+4y)^2\)
- \(\left(\frac{2}{5}m+\frac{3}{5}n\right)^2\)
- \((1+0{,}1x)^2\)
1. \[ (x+2)^2=x^2+2(x)(2)+2^2=x^2+4x+4 \]
2. \[ (3+a)^2=3^2+2(3)(a)+a^2=9+6a+a^2 \]
3. \[ (m+n)^2=m^2+2mn+n^2 \]
4. \[ (2x+1)^2=(2x)^2+2(2x)(1)+1^2=4x^2+4x+1 \]
5. \[ (4+3y)^2=4^2+2(4)(3y)+(3y)^2=16+24y+9y^2 \]
6. \[ \left(\frac{1}{2}a+2\right)^2= \left(\frac{1}{2}a\right)^2+2\left(\frac{1}{2}a\right)(2)+2^2 =\frac{1}{4}a^2+2a+4 \]
7. \[ (0{,}5x+1{,}5)^2=(0{,}5x)^2+2(0{,}5x)(1{,}5)+(1{,}5)^2 =0{,}25x^2+1{,}5x+2{,}25 \]
8. \[ (x+y)^2=x^2+2xy+y^2 \]
9. \[ (2a+3b)^2=(2a)^2+2(2a)(3b)+(3b)^2=4a^2+12ab+9b^2 \]
10. \[ \left(m+\frac{1}{3}\right)^2=m^2+2m\left(\frac{1}{3}\right)+\left(\frac{1}{3}\right)^2 =m^2+\frac{2}{3}m+\frac{1}{9} \]
11. \[ (2{,}5+x)^2=(2{,}5)^2+2(2{,}5)(x)+x^2=6{,}25+5x+x^2 \]
12. \[ (3x+4y)^2=(3x)^2+2(3x)(4y)+(4y)^2=9x^2+24xy+16y^2 \]
13. \[ \left(\frac{2}{5}m+\frac{3}{5}n\right)^2= \left(\frac{2}{5}m\right)^2+ 2\left(\frac{2}{5}m\right)\left(\frac{3}{5}n\right)+ \left(\frac{3}{5}n\right)^2 \]
\[ =\frac{4}{25}m^2+\frac{12}{25}mn+\frac{9}{25}n^2 \]
14. \[ (1+0{,}1x)^2=1^2+2(1)(0{,}1x)+(0{,}1x)^2 =1+0{,}2x+0{,}01x^2 \]
Ojo con los paréntesis
Un error común ocurre en ejercicios como \((2x+1)^2\). Al calcular el primer término al cuadrado, debes elevar al cuadrado todo el término.
- Incorrecto: \(2x^2\)
- Correcto: \((2x)^2=4x^2\)
Recuerda usar paréntesis para evitar este error.
Factorizando un Trinomio Cuadrado Perfecto
Proceso inverso
Ahora haremos el proceso inverso. Si tenemos una expresión como \(a^2+2ab+b^2\), podemos contraerla a su forma original:
\[ a^2+2ab+b^2=(a+b)^2 \]
A este proceso se le llama factorizar.
Procedimiento para factorizar un trinomio cuadrado perfecto
Para factorizar \(x^2+6x+9\), seguimos estos pasos:
- Identificar las raíces de los extremos: la raíz cuadrada de \(x^2\) es \(x\), y la raíz cuadrada de \(9\) es \(3\).
- Verificar el término del medio: calculamos \(2\cdot x\cdot 3=6x\). Coincide con el término del medio.
- Escribir el resultado: como se cumplen las condiciones, la factorización es: \[ x^2+6x+9=(x+3)^2 \]
La clave está en el término del medio
Si al comprobar el término del medio el resultado no coincide, entonces el trinomio no es un cuadrado perfecto y no se puede factorizar con esta regla.
Ejemplo guiado: nivel 4
Factoricemos \(4x^2+20x+25\).
Paso 1: identificar las raíces de los extremos.
- La raíz de \(4x^2\) es \(2x\).
- La raíz de \(25\) es \(5\).
Paso 2: verificar el término del medio.
\[ 2(2x)(5)=20x \]
Coincide con el término del medio.
Paso 3: escribir el resultado.
\[ 4x^2+20x+25=(2x+5)^2 \]
Nivel 4: factorizar trinomios cuadrados perfectos
- \(x^2+4x+4\)
- \(a^2+6a+9\)
- \(m^2+10m+25\)
- \(4x^2+4x+1\)
- \(9y^2+24y+16\)
- \(\frac{1}{4}a^2+2a+4\)
- \(0{,}25x^2+1{,}5x+2{,}25\)
- \(x^2+2xy+y^2\)
- \(4a^2+12ab+9b^2\)
- \(m^2+\frac{2}{3}m+\frac{1}{9}\)
- \(6{,}25+5x+x^2\)
- \(9x^2+24xy+16y^2\)
- \(\frac{4}{25}m^2+\frac{12}{25}mn+\frac{9}{25}n^2\)
- \(1+0{,}2x+0{,}01x^2\)
1. Raíces: \(x\) y \(2\). Como \(2(x)(2)=4x\), entonces: \[ x^2+4x+4=(x+2)^2 \]
2. Raíces: \(a\) y \(3\). Como \(2(a)(3)=6a\), entonces: \[ a^2+6a+9=(a+3)^2 \]
3. Raíces: \(m\) y \(5\). Como \(2(m)(5)=10m\), entonces: \[ m^2+10m+25=(m+5)^2 \]
4. Raíces: \(2x\) y \(1\). Como \(2(2x)(1)=4x\), entonces: \[ 4x^2+4x+1=(2x+1)^2 \]
5. Raíces: \(3y\) y \(4\). Como \(2(3y)(4)=24y\), entonces: \[ 9y^2+24y+16=(3y+4)^2 \]
6. Raíces: \(\frac{1}{2}a\) y \(2\). Como \(2\left(\frac{1}{2}a\right)(2)=2a\), entonces: \[ \frac{1}{4}a^2+2a+4=\left(\frac{1}{2}a+2\right)^2 \]
7. Raíces: \(0{,}5x\) y \(1{,}5\). Como \(2(0{,}5x)(1{,}5)=1{,}5x\), entonces: \[ 0{,}25x^2+1{,}5x+2{,}25=(0{,}5x+1{,}5)^2 \]
8. Raíces: \(x\) e \(y\). Como \(2(x)(y)=2xy\), entonces: \[ x^2+2xy+y^2=(x+y)^2 \]
9. Raíces: \(2a\) y \(3b\). Como \(2(2a)(3b)=12ab\), entonces: \[ 4a^2+12ab+9b^2=(2a+3b)^2 \]
10. Raíces: \(m\) y \(\frac{1}{3}\). Como \(2m\left(\frac{1}{3}\right)=\frac{2}{3}m\), entonces: \[ m^2+\frac{2}{3}m+\frac{1}{9}=\left(m+\frac{1}{3}\right)^2 \]
11. Ordenando: \[ 6{,}25+5x+x^2=x^2+5x+6{,}25 \] Raíces: \(x\) y \(2{,}5\). Como \(2(x)(2{,}5)=5x\), entonces: \[ 6{,}25+5x+x^2=(x+2{,}5)^2 \]
12. Raíces: \(3x\) y \(4y\). Como \(2(3x)(4y)=24xy\), entonces: \[ 9x^2+24xy+16y^2=(3x+4y)^2 \]
13. Raíces: \(\frac{2}{5}m\) y \(\frac{3}{5}n\). Como \[ 2\left(\frac{2}{5}m\right)\left(\frac{3}{5}n\right)=\frac{12}{25}mn \] entonces: \[ \frac{4}{25}m^2+\frac{12}{25}mn+\frac{9}{25}n^2= \left(\frac{2}{5}m+\frac{3}{5}n\right)^2 \]
14. Ordenando: \[ 1+0{,}2x+0{,}01x^2=0{,}01x^2+0{,}2x+1 \] Raíces: \(0{,}1x\) y \(1\). Como \(2(0{,}1x)(1)=0{,}2x\), entonces: \[ 1+0{,}2x+0{,}01x^2=(1+0{,}1x)^2 \]
Problemas de Aplicación
Ejemplo guiado: calculando un perímetro a partir del área
Una pequeña plaza cuadrada tiene un área de \(x^2+10x+25\) metros cuadrados. Si un jardinero quiere poner una cinta decorativa por todo el borde, ¿cuántos metros de cinta necesita?
Paso 1: entender el problema.
Nos dan el área y nos piden el perímetro. Para un cuadrado:
- \(\text{Área}=lado^2\)
- \(\text{Perímetro}=4\cdot lado\)
Paso 2: encontrar el lado.
Factorizamos el área:
\[ x^2+10x+25=(x+5)^2 \]
Entonces, el lado mide \(x+5\) metros.
Paso 3: calcular el perímetro.
\[ P=4(x+5)=4x+20 \]
El jardinero necesita \(4x+20\) metros de cinta.
Problema 1
El área de un cuadrado es \(x^2+6x+9\) unidades cuadradas. ¿Cuál es la longitud del lado del cuadrado en términos de \(x\)?
Factorizamos el área:
\[ x^2+6x+9=(x+3)^2 \]
Como el área de un cuadrado es \(lado^2\), entonces el lado corresponde a la base del cuadrado perfecto:
\[ lado=x+3 \]
La longitud del lado es \(x+3\) unidades.
Problema 2
Se quiere construir una piscina cuadrada rodeada por un borde de baldosas. El área total, piscina más borde, se puede expresar como \(4x^2+28x+49\) metros cuadrados. ¿Cuál es la expresión que representa la longitud del lado del área total?
Factorizamos el área total:
\[ 4x^2+28x+49=(2x+7)^2 \]
Verificación del término del medio:
\[ 2(2x)(7)=28x \]
Como el área total es un cuadrado perfecto, la longitud del lado del área total es:
\[ 2x+7 \]
El lado mide \(2x+7\) metros.
Problema 3
Un terreno cuadrado tiene un área de \(9x^2+30xy+25y^2\) metros cuadrados. Si se quiere cercar el terreno con una valla, ¿cuántos metros de valla se necesitan?
Primero factorizamos el área:
\[ 9x^2+30xy+25y^2=(3x+5y)^2 \]
Verificación del término del medio:
\[ 2(3x)(5y)=30xy \]
Entonces, el lado del terreno mide \(3x+5y\) metros.
El perímetro de un cuadrado es cuatro veces su lado:
\[ P=4(3x+5y) \]
\[ P=12x+20y \]
Se necesitan \(12x+20y\) metros de valla.