Homotecia - Página 1: Introducción y Proporcionalidad

Introducción

Imagina que tienes una linterna y proyectas la sombra de un objeto en la pared. Si acercas o alejas el objeto de la linterna, la sombra cambia de tamaño, ¿verdad? Eso es, en esencia, una homotecia. Es una transformación geométrica que "amplía" o "reduce" figuras, pero manteniendo su forma original. Piensa en ella como un "zoom" geométrico. La homotecia se define por un centro (como la linterna en nuestro ejemplo) y un factor (que nos dice cuánto agrandamos o achicamos), y está muy relacionada con la idea de proporcionalidad, que ya conoces.

Definición

Formalmente, decimos que una homotecia \(H_{O,k}\) es una transformación que, a partir de un punto fijo llamado centro (que llamaremos \(O\)), y un número llamado factor de homotecia (que llamaremos \(k\)), transforma cualquier punto \(P\) en otro punto \(P'\) que cumple dos condiciones:

1. \(O\), \(P\), y \(P'\) están en la misma línea recta. Es decir, si dibujas una línea que pasa por \(O\) y \(P\), el punto \(P'\) también estará en esa línea.
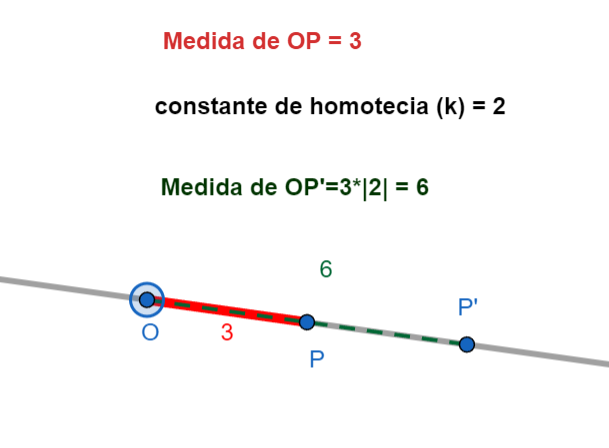
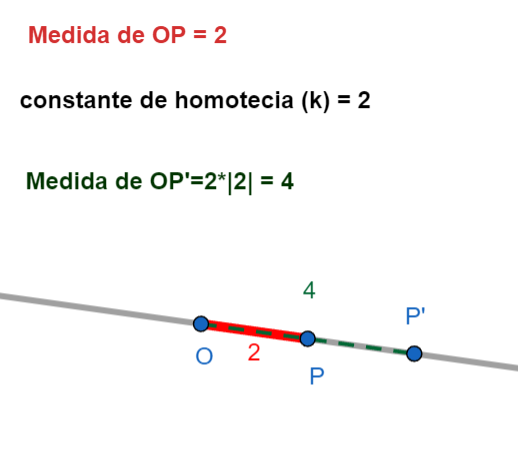
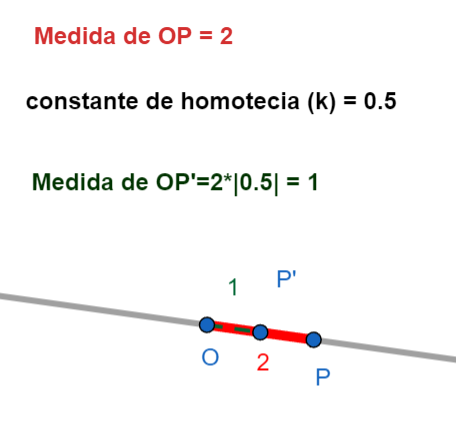
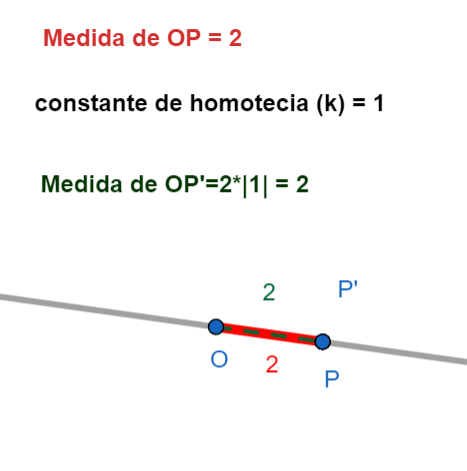
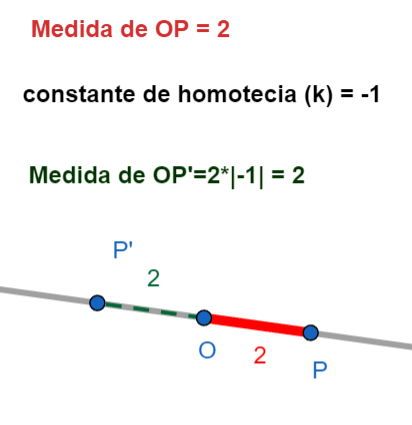
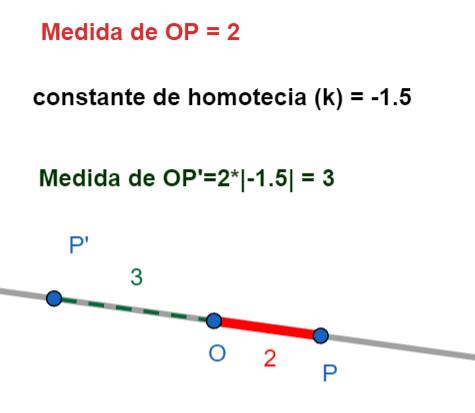
2. La distancia entre \(O\) y \(P'\) (que escribimos como \(OP'\)) es igual a la distancia entre \(O\) y \(P\) (que escribimos como \(OP\)) multiplicada por el valor absoluto de \(k\) (que escribimos como \(|k|\)). En símbolos: \(OP' = |k| \cdot OP\).

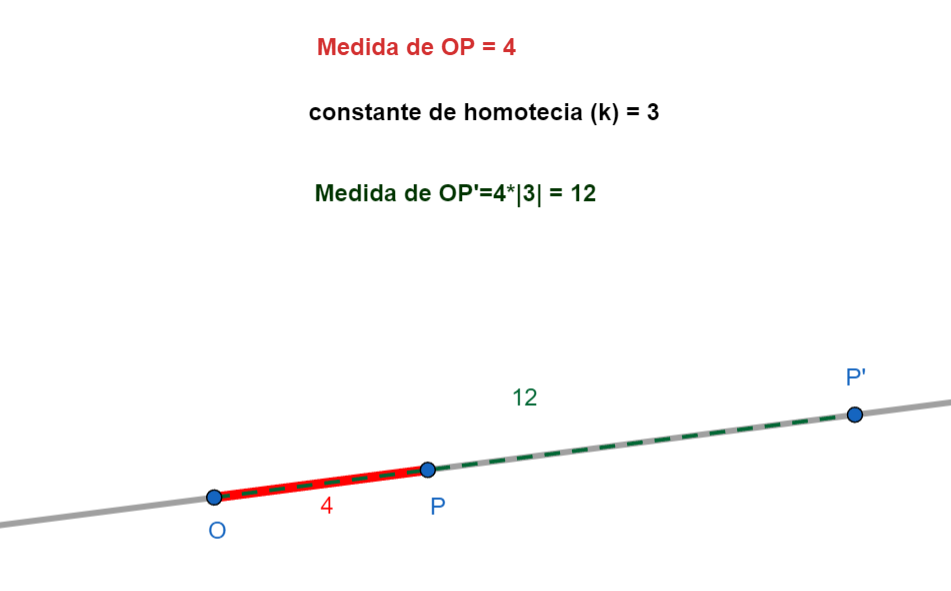
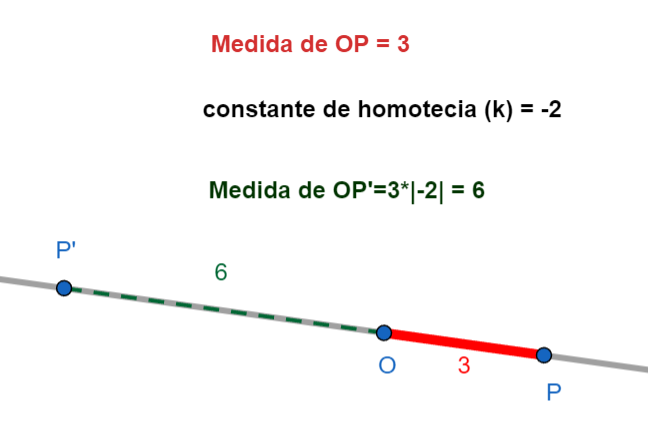
Importante: Si \(k\) es positivo, \(P'\) está en la misma dirección que \(P\) respecto a \(O\). Si \(k\) es negativo, \(P'\) está en la dirección *opuesta* a \(P\) respecto a \(O\). Imagina que la figura se "da vuelta" a través del centro.

Elementos Clave

Para entender bien la homotecia, hay tres conceptos fundamentales:

• Centro \(O\): Es como el punto de origen de la transformación, el punto desde donde "estiramos" o "encogemos" la figura. Es el único punto que no se mueve en la homotecia.
• Factor \(k\): Es un número que nos dice cuánto se agranda o se achica la figura.

	Si \(|k| > 1\), la figura se *agranda*. Por ejemplo, si \(k = 2\), la figura resultante será el doble de grande que la original.
	Si \(0 < |k| < 1\), la figura se *reduce*. Por ejemplo, si \(k = 0.5\) (o \(k = \frac{1}{2}\)), la figura resultante será la mitad de la original.
	Si \(k = 1\), la figura no cambia de tamaño. \(P\) y \(P'\) son el mismo punto.
	Si \(k = -1\), la figura se refleja con respecto al punto \(O\), y se mantiene del mismo tamaño.
	Si \(k\) es negativo, además de agrandar o achicar, la figura se *invierte* respecto al centro \(O\).

• Conservación de Ángulos y Proporcionalidad: La homotecia es especial porque:
  • Los ángulos de la figura *no cambian*. Si tenías un triángulo rectángulo, seguirá siendo rectángulo después de la homotecia.
  • Las longitudes de los lados *sí cambian*, pero lo hacen de forma proporcional. Todos los lados se multiplican por el mismo factor \(|k|\). Esto significa que la razón entre dos lados de la figura original es la misma que la razón entre los lados correspondientes en la figura transformada.
  • 
    

Ejemplos

Ejemplo 1: Ampliación

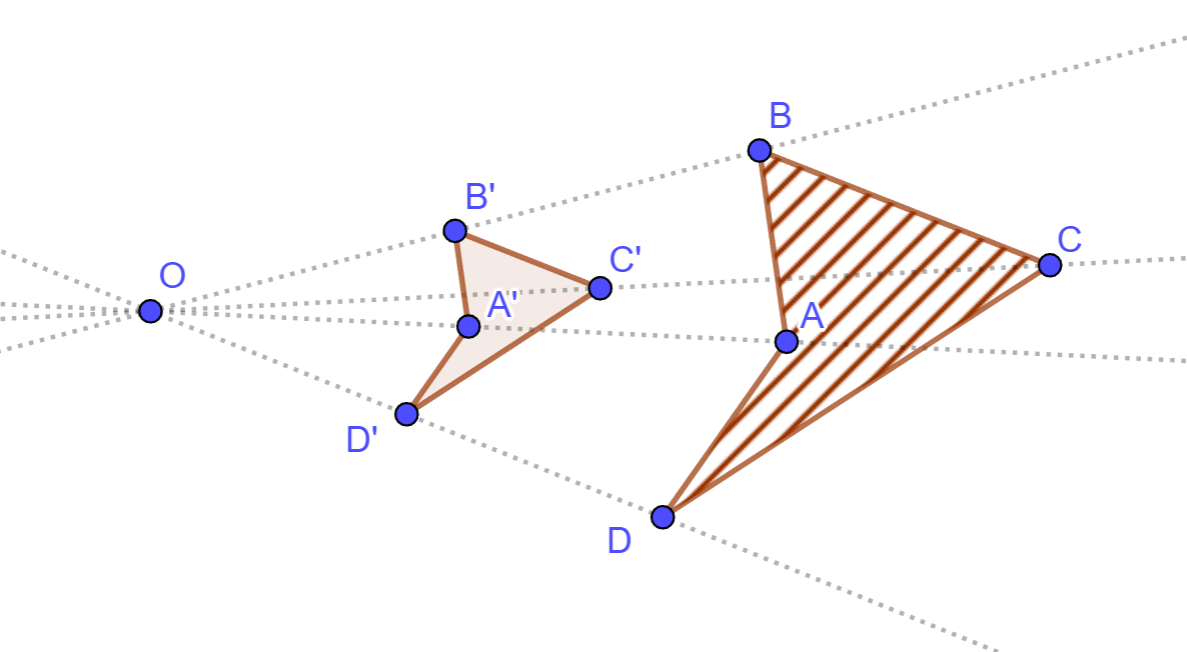
Tenemos un triángulo \(ABC\). Elegimos un punto \(O\) como centro de homotecia y un factor \(k = 2\). Para encontrar la imagen de cada vértice (los puntos \(A\), \(B\), y \(C\)), hacemos lo siguiente:

1. Dibujamos una línea recta desde \(O\) hasta \(A\).
2. Medimos la distancia \(OA\).
3. Multiplicamos esa distancia por 2 (porque \(k = 2\)).
4. Marcamos un punto \(A'\) sobre la línea \(OA\), pero a una distancia \(2 \cdot OA\) de \(O\).
5. Repetimos los pasos para los puntos \(B\) y \(C\), obteniendo \(B'\) y \(C'\).
6. Unimos \(A'\), \(B'\) y \(C'\) para obtener el triángulo \(A'B'C'\), que es el doble de grande que \(ABC\).

Ejemplo 2: Reducción e Inversión

Ahora, supongamos que tenemos un cuadrado y aplicamos una homotecia con centro \(O\) y factor \(k = -\frac{1}{2}\). Esto significa dos cosas:

• La figura se va a reducir a la mitad (porque \(|k| = \frac{1}{2}\)).
• La figura se va a invertir respecto a \(O\) (porque \(k\) es negativo).

Para construir la imagen, seguimos los mismos pasos que antes, pero al medir la distancia desde \(O\) a cada vértice, la dividimos entre 2 y marcamos el nuevo punto *al otro lado* de \(O\).

Ejemplo 3 (cotidiano): Una lupa. Cuando usas una lupa, estás aplicando una homotecia. El centro de la homotecia está aproximadamente en el centro de la lupa, y el factor de homotecia es mayor que 1 (por eso ves las cosas más grandes).

Práctica

Ahora vamos a practicar con algunos ejercicios. Los primeros tres son para que pienses en los conceptos, y los siguientes siete son para que apliques lo aprendido con dibujos y cálculos. Al final, hay cuatro problemas más desafiantes. ¡No te preocupes si al principio te cuesta, la práctica hace al maestro!

Ejercicios

1. (Conceptual) ¿Qué significa el factor de homotecia? Explica con tus propias palabras qué pasa si el factor es mayor que 1, y qué pasa si está entre 0 y 1. ¿Qué pasa si es negativo?

   Solución: El factor de homotecia, \(k\), es como el "control de zoom" de la transformación. Nos dice cuánto más grande o más pequeña será la figura transformada en comparación con la original.

   • Si \(|k| > 1\), la figura se agranda. Es como usar una lupa.
   • Si \(0 < |k| < 1\), la figura se reduce. Es como alejar un objeto: lo vemos más pequeño.
   • Si \(k\) es negativo, la figura se invierte respecto al centro \(O\), además de agrandarse o achicarse. Imagina que la figura "cruza" el centro y se da vuelta.
2. (Conceptual) La homotecia hace que las figuras cambien de tamaño, pero *no* cambia su forma. ¿Por qué?

   Solución: La forma de una figura está determinada por sus ángulos y por las *proporciones* entre sus lados. La homotecia conserva los ángulos (los deja iguales) y, aunque cambia el tamaño de los lados, los cambia a todos *en la misma proporción* (todos se multiplican por el mismo número, \(|k|\)). Como las proporciones se mantienen, la forma general no cambia.

3. (Conceptual) En la definición de homotecia, se dice que los puntos \(O\), \(P\), y \(P'\) están *alineados*. ¿Qué significa esto, y por qué es importante?

   Solución: Que estén alineados significa que los tres puntos están sobre la misma línea recta. Esto es importante porque nos dice que la transformación se hace "directamente hacia afuera" o "directamente hacia adentro" desde el centro \(O\). Cada punto y su imagen están conectados por una línea que pasa por el centro.

4. (Práctica) Dibuja un cuadrado de lado 2 cm en tu cuaderno. Luego, elige un punto fuera del cuadrado (ese será tu centro \(O\)). Aplica una homotecia con factor \(k = 3\). ¿Cuánto mide el lado del nuevo cuadrado?

   Solución:

   1. Desde el centro \(O\), traza líneas rectas que pasen por cada uno de los vértices del cuadrado original.
   2. Mide la distancia desde \(O\) a cada vértice.
   3. Multiplica cada una de esas distancias por 3 (porque \(k = 3\)).
   4. Marca los nuevos vértices (las imágenes) a esas distancias *triplicadas*, sobre las líneas que ya dibujaste.
   5. Une los nuevos vértices para formar el cuadrado ampliado.

   El lado del nuevo cuadrado medirá \(2 \text{ cm} \times 3 = 6 \text{ cm}\).

5. (Práctica) Piensa en objetos tecnologicos de la vida real. ¿Puedes nombrar uno que porduzca un  resultados similares a crear una homotecia con \(k > 1\)? Explica por qué.

   Solución: Un proyector de diapositivas o de cine es un buen ejemplo. La imagen pequeña en la diapositiva (o en el archivo digital) se agranda mucho al proyectarse en la pantalla. La lámpara del proyector actúa como el centro de homotecia, y la distancia entre la lámpara y la pantalla determina el factor de ampliación. Otro ejemplo es una lupa: la lupa (centro de la homotecia) agranda la imagen del objeto que estás observando.

6. (Práctica) Tienes un triángulo. Quieres construir su imagen con una homotecia de factor \(k = \frac{1}{2}\), usando regla y compás. Describe paso a paso cómo lo harías.

   Solución:

   1. Elige un punto cualquiera como centro \(O\).
   2. Dibuja líneas rectas desde \(O\) hasta cada uno de los vértices del triángulo (llamémoslos \(A\), \(B\), y \(C\)).
   3. Mide la distancia \(OA\).
   4. Divide esa distancia entre 2 (porque \(k = \frac{1}{2}\)).
   5. Marca un punto \(A'\) sobre la línea \(OA\), a la distancia \(OA/2\) de \(O\).
   6. Repite los pasos 3, 4 y 5 para los puntos \(B\) y \(C\), obteniendo \(B'\) y \(C'\).
   7. Une \(A'\), \(B'\), y \(C'\) para formar el triángulo reducido. Este triángulo será exactamente la mitad del tamaño del original, y estará en la misma orientación.
7. (Práctica) Un punto \(P\) está a 5 cm de un punto \(O\). Aplicamos una homotecia con centro \(O\) y factor \(k = 2\). ¿A qué distancia de \(O\) quedará el punto imagen \(P'\)?

   Solución: La distancia \(OP'\) será igual a la distancia \(OP\) multiplicada por \(|k|\). En este caso, \(OP' = 5 \text{ cm} \times 2 = 10 \text{ cm}\). El punto \(P'\) quedará a 10 cm de \(O\).

8. (Práctica) Imagina que aplicas una homotecia a una figura usando un factor \(k = 0\). ¿Qué le pasa a la figura? Explica y da un ejemplo sencillo.

   Solución: Si \(k = 0\), *todos* los puntos de la figura se transforman en el centro \(O\). La figura "desaparece" o, más precisamente, se colapsa en un solo punto. Por ejemplo, si tienes un triángulo \(ABC\) y aplicas una homotecia con centro \(O\) y \(k = 0\), los puntos \(A'\), \(B'\), y \(C'\) *todos* coincidirán con \(O\). El triángulo se convierte en un punto.

9. (Práctica) Dibuja dos líneas rectas que se crucen en un punto \(O\). Marca un punto \(P\) en una de las líneas. Ahora, aplica una homotecia con centro \(O\) y factor \(k = -2\). Describe cómo encontrarías la posición del punto imagen \(P'\).

   Solución:

   1. Mide la distancia \(OP\).
   2. Multiplica esa distancia por 2 (porque \(|k| = 2\)).
   3. Como \(k\) es negativo, \(P'\) estará en la *dirección opuesta* a \(P\) respecto a \(O\). Es decir, \(P'\) estará en la misma línea que \(O\) y \(P\), pero *al otro lado* de \(O\).
   4. Marca el punto \(P'\) a una distancia \(2 \cdot OP\) de \(O\), pero en el lado opuesto a \(P\).
10. (Práctica) Piensa en un experimento donde usas una linterna para proyectar la sombra de un objeto (por ejemplo, un bloque de madera) sobre una pared. ¿De qué manera determinarías en este experimento el factor de homotecia de la sombra?

    Solución: En este experimento, la linterna es el centro de homotecia. El factor de homotecia está determinado por la *relación entre las distancias*. Específicamente:

    • Distancia de la linterna al objeto (bloque).
    • Distancia de la linterna a la pared.

    Si llamamos \(d_1\) a la distancia de la linterna al objeto, y \(d_2\) a la distancia de la linterna a la pared, entonces el valor absoluto del factor de homotecia es \(|k| = \frac{d_2}{d_1}\). Si la pared está más lejos de la linterna que el objeto (\(d_2 > d_1\)), entonces \(|k| > 1\) y la sombra será más grande que el objeto. Si acercas el objeto a la linterna (disminuyendo \(d_1\)), la sombra también se agranda.

Problemas

Estos problemas son un poco más difíciles. ¡Intenta resolverlos usando todo lo que has aprendido!

1. Un triángulo \(ABC\) tiene sus vértices a las siguientes distancias del centro de homotecia \(O\): \(OA = 3\) cm, \(OB = 4\) cm, y \(OC = 5\) cm. Si aplicamos una homotecia con centro \(O\) y factor \(k = 2\), ¿a qué distancias de \(O\) quedarán los vértices del triángulo transformado (\(A'\), \(B'\), y \(C'\))?

   Solución: Como el factor de homotecia es 2, todas las distancias desde el centro se duplican. Por lo tanto:

   • \(OA' = 2 \cdot OA = 2 \cdot 3 \text{ cm} = 6 \text{ cm}\)
   • \(OB' = 2 \cdot OB = 2 \cdot 4 \text{ cm} = 8 \text{ cm}\)
   • \(OC' = 2 \cdot OC = 2 \cdot 5 \text{ cm} = 10 \text{ cm}\)

   Los vértices del triángulo transformado quedarán a 6 cm, 8 cm y 10 cm de \(O\), respectivamente.

2. Dibuja un ejemplo de una homotecia con factor \(k = -3\). Elige una figura sencilla (como un triángulo o un cuadrado) y un centro de homotecia \(O\). Muestra claramente cómo la figura se agranda y se invierte.

   Solución (Guía):

   1. Dibuja un triángulo (o cuadrado) en tu cuaderno.
   2. Elige un punto \(O\) como centro de homotecia. Puede estar dentro o fuera de la figura, pero para que la inversión se vea más clara, es mejor elegirlo fuera.
   3. Dibuja líneas rectas desde \(O\) hasta cada uno de los vértices de la figura original.
   4. Mide la distancia desde \(O\) a cada vértice.
   5. Multiplica cada una de esas distancias por 3 (porque \(|k| = 3\)).
   6. Como \(k\) es negativo, marca los nuevos vértices (las imágenes) a esas distancias *triplicadas*, pero *al otro lado* de \(O\), sobre las líneas que ya dibujaste.
   7. Une los nuevos vértices para formar la figura transformada. Verás que la figura es tres veces más grande que la original y está "dada vuelta" con respecto a \(O\).
3. Un compañero de clase dice que "la homotecia cambia la forma de un rectángulo". ¿Cómo le demostrarías, con medidas y un ejemplo, que está equivocado?

   Solución: Para demostrar que la homotecia *no* cambia la forma, necesitamos mostrar que los ángulos se mantienen iguales y que las proporciones entre los lados también se mantienen. Podemos hacer lo siguiente:

   1. Dibuja un rectángulo. Mide sus ángulos (todos deben ser de 90 grados). Mide la longitud de sus lados (largo y ancho).
   2. Calcula la *razón* entre el largo y el ancho del rectángulo original (divide el largo entre el ancho).
   3. Aplica una homotecia al rectángulo (elige un centro \(O\) y un factor \(k\), por ejemplo, \(k = 2\)).
   4. Mide los ángulos del rectángulo transformado (deberían seguir siendo de 90 grados).
   5. Mide los lados del rectángulo transformado.
   6. Calcula la razón entre el largo y el ancho del rectángulo transformado. Esta razón debe ser *igual* a la razón que calculaste en el paso 2.

   Si los ángulos se mantienen y la razón entre los lados se mantiene, entonces la forma no ha cambiado; solo el tamaño.

4. En un plano, un punto \(P\) está a 2.5 cm de un punto \(O\). Primero, aplicamos una homotecia con centro \(O\) y factor \(k = 4\). Luego, al resultado de *esa* homotecia, le aplicamos *otra* homotecia, también con centro \(O\), pero con factor \(k = \frac{1}{4}\). ¿Dónde termina el punto \(P\) después de estas dos transformaciones?

   Solución:

   *Primera homotecia:* Después de la primera homotecia, el punto \(P\) se transforma en un punto \(P'\) que está a una distancia \(OP' = 2.5 \text{ cm} \times 4 = 10 \text{ cm}\) de \(O\).

   *Segunda homotecia:* Ahora, aplicamos una homotecia a \(P'\) con factor \(\frac{1}{4}\). El punto resultante, llamémoslo \(P''\), estará a una distancia \(OP'' = 10 \text{ cm} \times \frac{1}{4} = 2.5 \text{ cm}\) de \(O\).

   ¡El punto \(P''\) está en la misma posición que el punto original \(P\)! Esto sucede porque las dos homotecias "se cancelan" entre sí. Multiplicar por 4 y luego por \(\frac{1}{4}\) es lo mismo que multiplicar por 1.