Correspondencia de segmentos y Primer Teorema de Tales

Segmentos correspondientes:

Sean dos rectas L₁ y L₂ que se cortan en un punto (secan). Si estas rectas son atravesadas por dos o más transversales (en la imagen, AB, CD, EF), diremos que se forman segmentos correspondientes, que son los trazos en L₁ y L₂ delimitados por las mismas transversales.

Ejemplo:

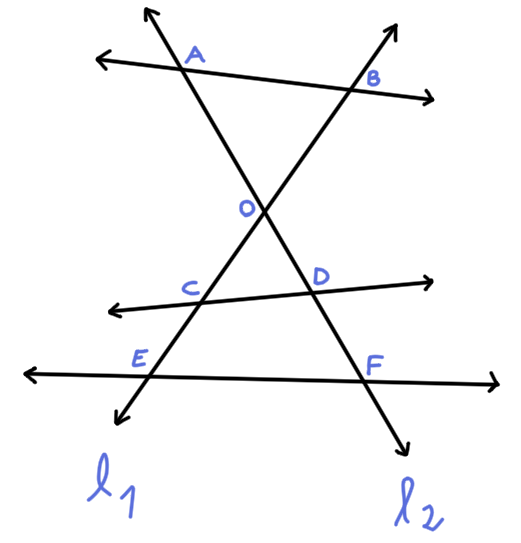
Bajo estas condiciones, son segmentos correspondientes:

• \(\overline{OA}\) y \(\overline{OB}\)
• \(\overline{OC}\) y \(\overline{OD}\)
• \(\overline{OE}\) y \(\overline{OF}\)
• \(\overline{CE}\) y \(\overline{DF}\)
• \(\overline{AD}\) y \(\overline{BC}\)
• \(\overline{AF}\) y \(\overline{BE}\)

PRIMER TEOREMA DE TALES

Teorema: Rectas paralelas determinan segmentos correspondientes proporcionales.

Hipótesis: \(\overline{AB} \parallel \overline{CD}\)

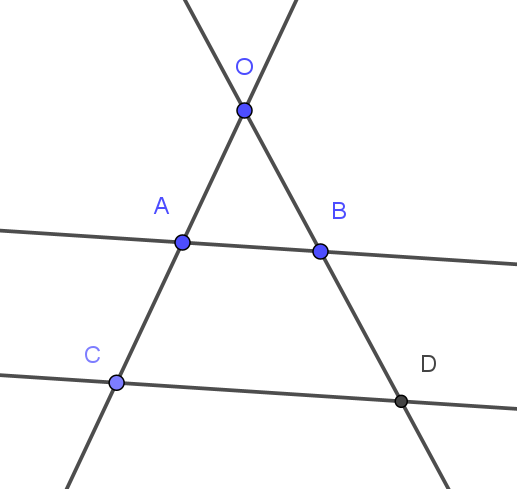
Tesis:

1. \(\displaystyle \frac{\overline{OA}}{\overline{AC}} = \frac{\overline{OB}}{\overline{BD}}\)
2. \(\displaystyle \frac{\overline{OC}}{\overline{OA}} = \frac{\overline{OD}}{\overline{OB}}\)
3. \(\displaystyle \frac{\overline{OC}}{\overline{AC}} = \frac{\overline{OD}}{\overline{BD}}\)

Demostración (Tesis 1):

Probemos \(\frac{\overline{OA}}{\overline{AC}} = \frac{\overline{OB}}{\overline{BD}}\).

I. Consideremos los triángulos \(ABO\) y \(CBA\). Ambos tienen la misma altura \(h\). Entonces:

\[ A(\triangle ABO) = \frac{\overline{OA} \cdot h}{2}, \quad A(\triangle CBA) = \frac{\overline{AC} \cdot h}{2}. \]

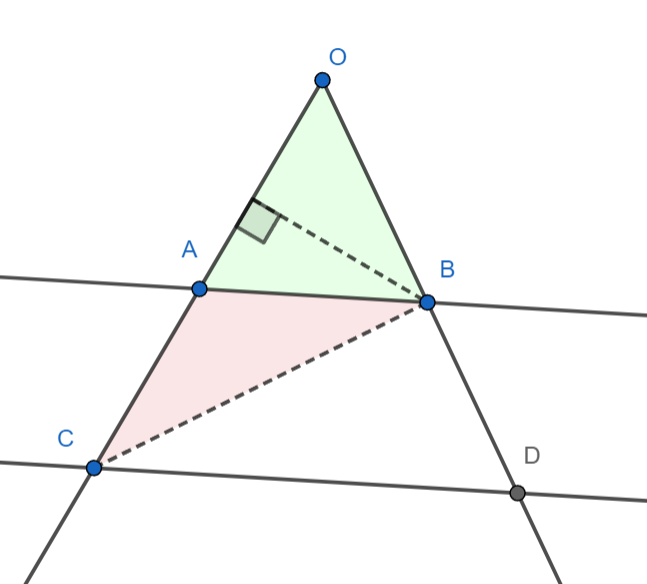
Haciendo el cociente entre ambas áreas: \[ \frac{A(\triangle ABO)}{A(\triangle CBA)} = \frac{\frac{\overline{OA}\cdot h}{2}}{\frac{\overline{AC}\cdot h}{2}} = \frac{\overline{OA}}{\overline{AC}}. \]

II. Análogamente, si seguimos pasos similares en los triángulos \(ABO\) y \(DAB\), obtenemos:

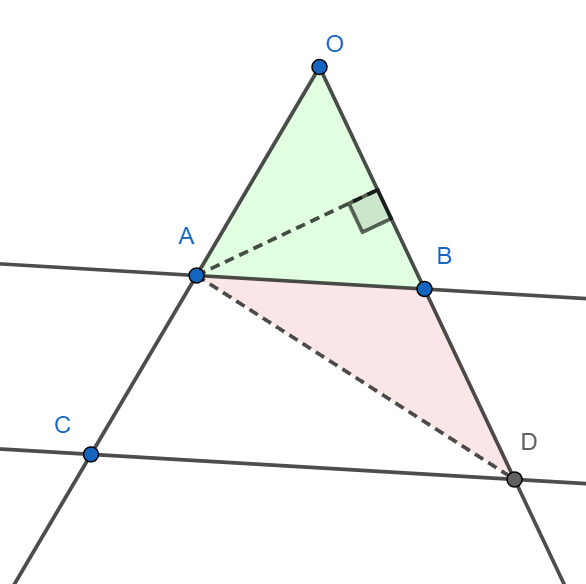
\[ \frac{A(\triangle ABO)}{A(\triangle DAB)} = \frac{\overline{OB}}{\overline{BD}}. \]

III. Los triángulos \(CBA\) y \(DAB\) tienen el lado \(\overline{AB}\) en común y la misma altura correspondiente a ese lado, pues \(\overline{AB} \parallel \overline{CD}\). Por lo tanto, \(A(\triangle CBA) = A(\triangle DAB)\).

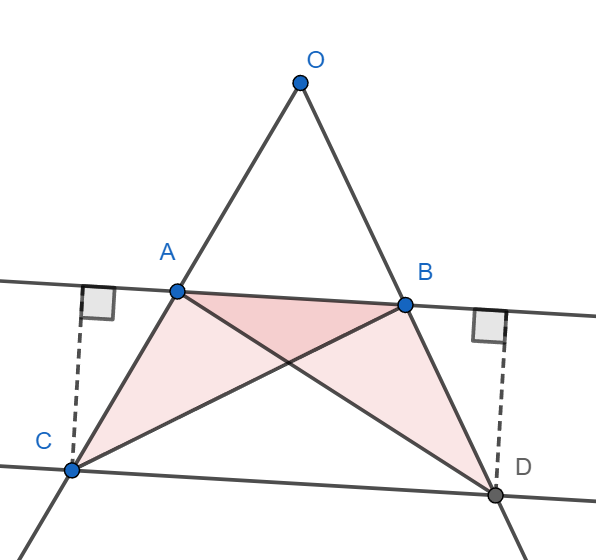
IV. De I, II y III se deduce:

\[ \frac{\overline{OA}}{\overline{AC}} = \frac{A(\triangle ABO)}{A(\triangle CBA)} = \frac{A(\triangle ABO)}{A(\triangle DAB)} = \frac{\overline{OB}}{\overline{BD}}. \]

Por consiguiente: \[ \frac{\overline{OA}}{\overline{AC}} = \frac{\overline{OB}}{\overline{BD}} \quad (\text{Q.E.D.}) \]

Si todavía no estás convencido de la proporcionalidad de las áreas, puedes mover levemente los puntos en la siguiente figura interactiva y observar qué sucede:

Con triángulos opuestos por el vértice

Este teorema también se cumple si las paralelas cortan las prolongaciones del ángulo más allá del vértice.

Hipótesis: \(\overline{RS} \parallel \overline{PQ}\)

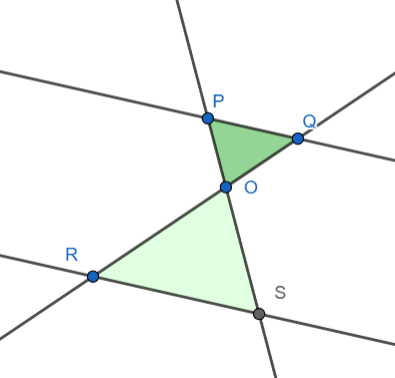
Tesis:

\(\displaystyle \frac{OP}{OS} = \frac{OQ}{OR}\), \(\quad \frac{OP}{PS} = \frac{OQ}{QR}, \quad \frac{OS}{PS} = \frac{OR}{QR}. \)

Para probarlo, basta un giro de 180° en torno al punto O para que la figura quede reducida al caso anterior (ya demostrado).

En la siguiente visualización podemos confirmarlo. Mueve la barra de 0° a 180° y viceversa para observar las proporciones (notando que las razones se forman entre segmentos colineales).

Corolario

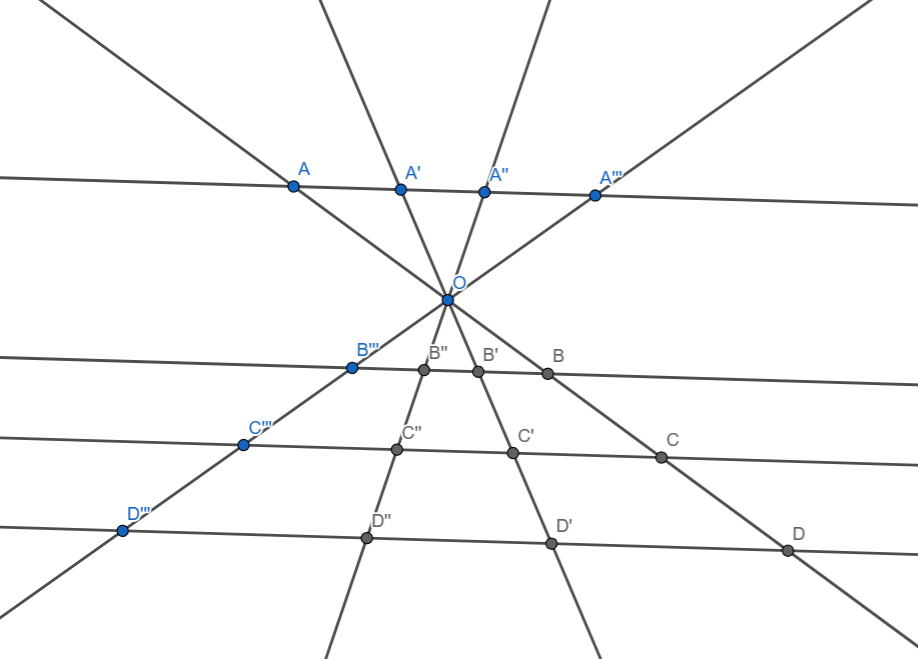
Los segmentos correspondientes, determinados al cortar un haz de rectas por tres o más paralelas, son proporcionales.

\[ \frac{OA}{OB} = \frac{OA'}{OB'} = \frac{OA''}{OB''} = \frac{OA'''}{OB'''} \]
\[ \frac{AB}{CD} = \frac{A'B'}{C'D'} = \frac{A''B''}{C''D''} = \frac{A'''B'''}{C'''D'''} \]
\[ \frac{OC}{OB} = \frac{OC'}{OB'} = \frac{OC''}{OB''} = \frac{OC'''}{OB'''} \]

Así podemos escribir muchas otras proporciones.